방접원과 내접원의 반지름을 이용한 관계식과 헤론의 공식 유도 : 네이버 블로그 (naver.com)
방접원과 내접원의 반지름을 이용한 관계식과 헤론의 공식 유도
안녕하세요 월조입니다 :) 오늘은 방접원의 반지름과 내접원의 반지름 사이의 관계식에 대해서 포스팅해보...
blog.naver.com
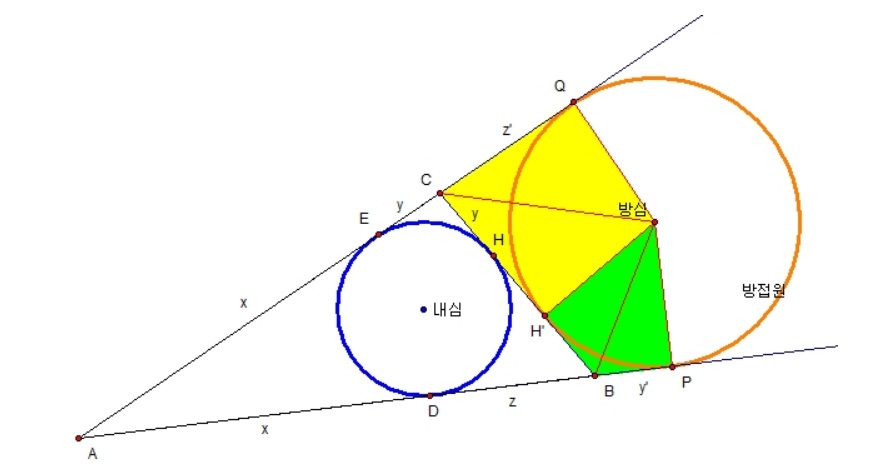
1. 방접원의 성질
접선의 길이는 서로 같기 때문에 CE = CH이고 BH = BD이고 AD = AE이다.
그러므로 삼각형 ABC의 둘레는 2(x+y+z)가 된다.

여기서 BP = y'이고 CQ = z'이라고 하자.
원의 접선, 원의 접선의 길이 – 수학방 (mathbang.net)
원의 접선, 원의 접선의 길이
현에 대한 두 번째로 현의 길이에 대한 내용입니다. 원에 대해서 계속하고 있는데, 생각보다 어렵지 않죠? 새 단원의 시작이라서 그래요. 이 글도 별로 어렵지 않아요. 이번에는 현과는 조금은
mathbang.net
당연하게도 원 밖의 한 점 C에서 방점의 접선 CQ = CH'이고 B에서 BP = BH'인데.. 왜 그런지 잠깐만 생각해보면
방심을 O라 하고 H', P까지의 거리는 방접원의 반지름으로 같다
그리고 방심과 접선이 이루는 각 BPO는 90'이고 BH'O도 90'이다.
그리고 빗변 BO가 서로 같다.
따라서 초록색 삼각형 BOP와 BOH'은 RHS 합동이다
직각삼각형은 빗변이 서로 같고 한 예각의 크기가 서로 같으면 합동(RHA합동)
혹은 빗변이 서로 같고 다른 한 변의 길이가 서로 같으면 합동(RHS 합동)
직각삼각형의 합동, 직각삼각형의 합동 조건 – 수학방 (mathbang.net)
직각삼각형의 합동, 직각삼각형의 합동 조건
이번 글에서는 직각삼각형에 대해서 공부할 거예요. 직각삼각형이란 무엇인지 두 직각삼각형이 합동이 되려면 어떤 조건이 있는지요. 먼저 삼각형의 합동 조건을 혹시 기억하고 있나요? 삼각형
mathbang.net
따라서 다음과 같은 항등식을 얻는다
BC = BH' + H'C = BH + CH
이 때 BC = y+z이고, BH' + CH' = y'+z'
따라서, y+z = y'+z'
다음 점 A에서 방심까지 하나의 직선을 그어 다음과 같은 그림을 만들어보자.
참고로 "점 A, 내심, 방심은 한 직선위에 있다는 성질이 있다"

방심을 O라고 하면 AOQ와 AOP는 서로 RHS합동이다.
그러므로 AP = AQ이다.
따라서, x+z+y' = x+y+z'
첫번째 식 y+z = y'+z'과 비교해보면...
$$y' - z' = y - z$$
$$y' + z' = y + z$$
따라서, 연립하면 y = y'이고 z = z'이다.

삼각형의 변의 길이가 각각 a,b,c라면 삼각형의 둘레는 a+b+c = 2(x+y+z)
여기서 $$ s = \frac{a+b+c}{2} = x+y+z $$ 라고 하자.
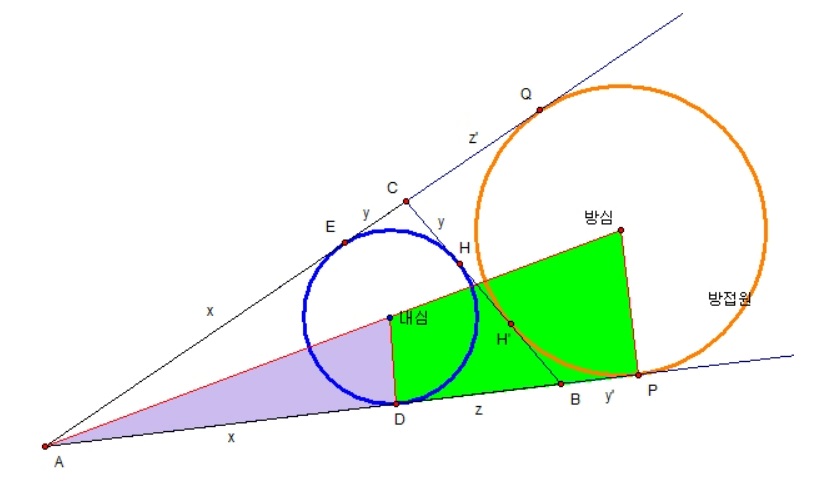
이때 내심을 I라 하고 방심을 O라 하면 OAP와 IAD는 서로 AA닮음이다.
왜냐하면 IAD = OAP이고 IDA = OPA = 90'이기 때문이다.
그러므로 ID : IP = AD: AP
여기서 ID = (내접원의 반지름) = r , IP = 방접원의 반지름 = $r_{a}$
AD = x이고 AP = x+y+z이다.
그러므로 r(x+y+z) = $xr_{a}$
그런데, y+z = a이다. (변 BC의 길이)
따라서, $$\frac{r}{r_{a}}= \frac{s - a}{s}$$
CA에 접하는 방접원에서도 다음과 같은 식이 유도될 것이다.
$$r: r_{b} = z: x+y+z$$
여기서 x+y = b이므로...(선분 AC의 길이)
그러므로 $$\frac{r}{r_{b}} = \frac{s-b}{s}$$
그리고 AB에 접하는 방접원에서도...
$$r:r_{c} = y:x+y+z$$
여기서 x+z = c이므로... (선분 AB의 길이)
$$\frac{r}{r_{c}} = \frac{s-c}{s}$$
내접원의 반지름과 방접원의 반지름 $r_{a}$ , $r_{b}$, $r_{c}$의 세 관계식
$$\frac{r}{r_{a}}= \frac{s - a}{s}$$
$$\frac{r}{r_{b}} = \frac{s-b}{s}$$
$$\frac{r}{r_{c}} = \frac{s-c}{s}$$
전부 더한다면.... $\frac{r}{r_{a}}$ + $\frac{r}{r_{b}}$ + $\frac{r}{r_{b}}$ = $\frac{3s-a-b-c}{s}$
$ s = \frac{a+b+c}{2} = x+y+z $가 성립하므로... $\frac{3s-a-b-c}{s} = 1$
그러므로.. $\frac{r}{r_{a}}$ + $\frac{r}{r_{b}}$ + $\frac{r}{r_{b}}$ = 1
양변을 내접원의 반지름 r로 나눈다면...
$$\frac{1}{r_{a}} + \frac{1}{r_{b}} + \frac{1}{r_{c}} = \frac{1}{r}$$
방접원의 세 반지름 각각의 역수의 합은 내접원의 반지름의 역수와 같다
2. 연습문제
16481번: 원 전문가 진우 (acmicpc.net)
16481번: 원 전문가 진우
첫째 줄에 r1, r2, r3의 값이 사이에 공백을 한 개씩 두고 차례대로 주어진다. 주어지는 모든 수는 1,000 이하의 양의 정수이다.
www.acmicpc.net
3. 풀이
위에서 얻은 최종 식, "내접원의 반지름의 역수는 세 방접원의 반지름의 역수의 합과 같다"에 대입하여 내접원의 반지름을 구한다
from sys import stdin
r1,r2,r3 = map(int,stdin.readline().split())
print(1/(1/r1 + 1/r2 + 1/r3))
'기하학' 카테고리의 다른 글
| 기하학 알고리즘의 기본 - 두 벡터의 외적(cross product)에 대하여 (0) | 2023.08.05 |
|---|---|
| 나비 정리(butterfly theorem) (0) | 2023.03.21 |
| 컴퓨터로 원의 둘레를 추적하면서 개수를 세는 방법 (0) | 2023.03.10 |
| 삼각형의 내각의 이등분선과 외각의 이등분선 정리 (0) | 2023.03.09 |
| 스튜어트의 정리(Stewart's theorem) (0) | 2023.03.08 |

