1. 문제
1709번: 타일 위의 원
한 변의 길이가 1cm인 정사각형 모양의 타일이 있다. 이 타일들이 큰 정사각형을 빈틈없이 채우고 있는데, 정사각형의 한 변의 길이는 짝수이다. 이 한 변의 길이를 Ncm이라고 하자. 큰 정사각형에
www.acmicpc.net
2. 풀이
규칙이 있나 했는데 논리로 개수를 셀 수 있는 문제였다
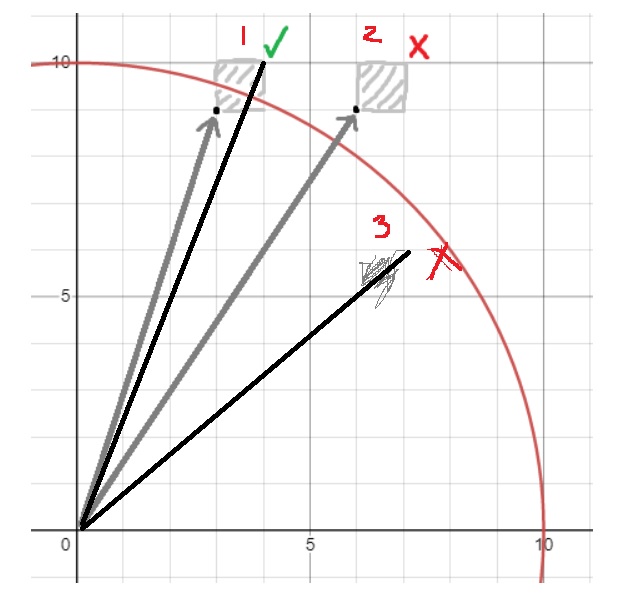
위 그림과 같이 1*1 타일에 대하여, 좌측 하단의 점까지 거리와 우측 상단의 점까지 거리를 구해보고..
그 거리와 원의 반지름을 비교해본다.
타일 위에 원의 둘레가 존재한다는 것은, "좌측 하단의 점까지 거리 < 원의 반지름 < 우측 상단의 점까지 거리"
"원의 반지름 >= 우측 상단의 점까지 거리" 이거나 "원의 반지름 <= 좌측 하단의 점까지 거리"이면.. 원의 둘레가 존재하지 않는다
그러면 타일의 개수는 어떻게 세야할까
가장 쉽게는 모든 타일을 조사해보는 방법이 있을 것 같다
원의 중심을 원점이라 하면, 원의 반지름은 전체 정사각형의 한변의 길이의 절반이 될 것이다.
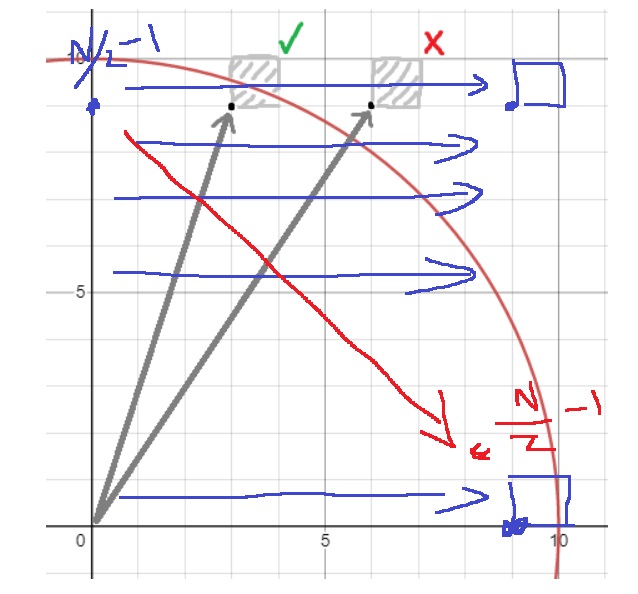
이때, 원은 1/4로 서로 대칭이므로 사분면 하나만 조사하면 될 것이다.
맨 좌측 상단의 점 (0,(n/2)-1)이 "좌측 하단의 점"인 사각형에 대해, 조사를 시작한다
"좌측 하단의 점"인 (0,(n/2)-1)까지 거리, 그러면 "우측 상단의 점"의 좌표는 어떻게 구할까?
현재 "좌측 하단의 점"에 대해 x좌표에 1을 더하고 y좌표에 1을 더하면 될 것이다
(1,(n/2))와의 거리를 구한 다음에, 원의 반지름과 비교해본다.
이런식으로 모든 x,y에 대해, x가 (n/2)-1이고 y가 0일때까지 우측 하단으로 훑으면서 원의 둘레가 타일 위에 있을 조건을 하나씩 조사해보면 될 것이다.
from sys import stdin
n = int(stdin.readline())
n = n//2
r2 = (n)**2
count = 0
for y in range(n-1,-1,-1):
for x in range(0,n):
down = x**2+y**2
up = (x+1)**2+(y+1)**2
if r2 > down and r2 < up:
count += 1
print(count*4)
근데 n이 150,000,000까지라서, $O(n^{2})$인 이 코드가 시간안에 돌아갈리가 없다..
하나 다른 방법은 모든 경우를 조사할 필요가 있을까?에서 출발한다
당연히 아닌 곳은 처음부터 보지 않으면 안될까?
좌측 상단부터 쭉 훑어가기 시작하다가...
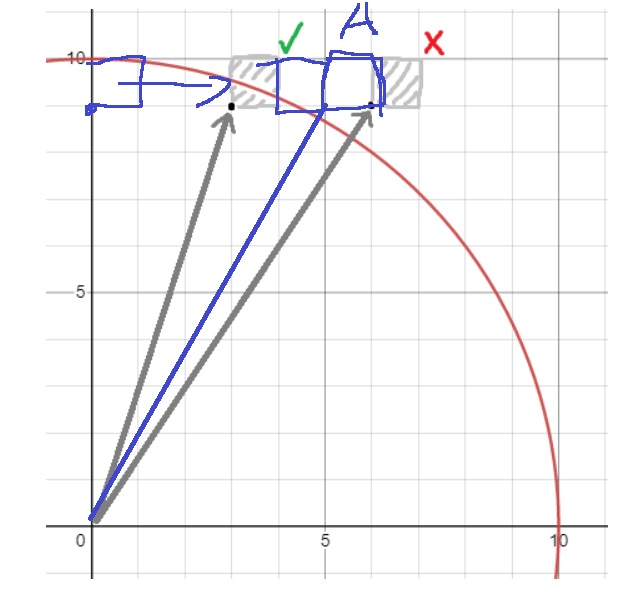
"좌측 하단까지의 거리"가 원의 반지름 이상이 된 순간 그 뒤는 굳이 안봐도 된다
그리고 바로 아래줄로 내려가서 다시 우측으로 이동하면서 훑어보면 된다.
그러다가 또 "좌측 하단까지의 거리"가 원의 반지름 이상이 된다면 다시 아래줄로 이동한다
이를 반복한다면 조사해야하는 경우가 줄어들 것이다

위와 같이 진짜로 원의 둘레만 따라가보자는 것이다
근데 이제 "좌측 하단까지의 거리"가 원의 반지름 이상이 된 경우 바로 아래줄로 내려가면..
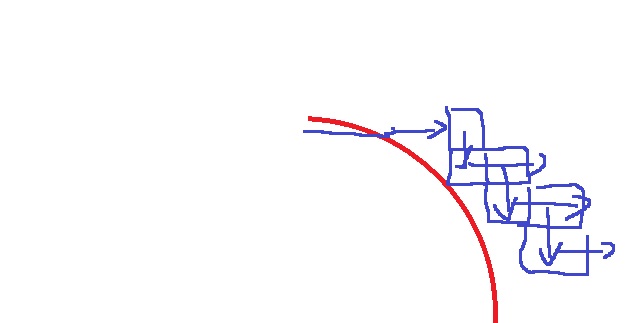
어떤 경우는 위와 같이 바로 아래줄에도 원의 둘레가 없어가지고,
실제로 그 아래줄의 왼쪽에는 원의 둘레가 있는데 오른쪽, 아래로만 계속 가다보니까
왼쪽의 원의 둘레가 있는 타일을 세지 못하는 경우가 있다는 것
따라서 "좌측 하단까지의 거리"가 원의 반지름 이상인 경우
1칸 왼쪽으로 x좌표를 이동한 다음에 아래줄로 이동시킨다(y좌표를 1 감소 시킨다)
from sys import stdin
n = int(stdin.readline())
n = n//2
r2 = (n)**2
count = 0
start = 0
for y in range(n-1,-1,-1):
for x in range(start,n):
down = x**2+y**2
up = (x+1)**2+(y+1)**2
if r2 > down and r2 < up:
count += 1
elif down >= r2:
start = x-1
break
print(count*4)
1709 타일 위의 원
https://www.acmicpc.net/problem/1709 1709번: 타일 위의 원 한 변의 길이가 1cm인 정사각형 모양의 타일이 있다. 이 타일들이 큰 정사각형을 빈틈없이 채우고 있는데, 정사각형의 한 변의 길이는 짝수이다.
10cheon00.tistory.com
'기하학' 카테고리의 다른 글
| 나비 정리(butterfly theorem) (0) | 2023.03.21 |
|---|---|
| 삼각형의 내접원의 반지름과 방접원의 반지름의 관계식 (0) | 2023.03.10 |
| 삼각형의 내각의 이등분선과 외각의 이등분선 정리 (0) | 2023.03.09 |
| 스튜어트의 정리(Stewart's theorem) (0) | 2023.03.08 |
| 겹치는 직사각형의 넓이를 조건문 없이 구하기 (0) | 2023.03.06 |

