1. 내각의 이등분선
삼각형의 한 내각을 이등분한 경우 다음과 같을때,
a:b = c:d가 성립한다

다음과 같이 선분 AD에 평행하게 EC를 긋고, BA의 연장선과 EC의 교점이 E라고 한다면...
각 BAD = 각 BEC이다.

그러므로 그림과 같이 ACE가 이등변삼각형이고, AC = AE가 된다.
이 때, 삼각형 BAD와 삼각형 BEC는 서로 닮았다.
따라서 BA: AE = BD: DC이다.
그러므로 a:b = c:d
2. 외각의 이등분선
삼각형의 한 외각의 이등분선에 대해 다음 상황에서 a:b = c:d이다.

다음과 같이 삼각형 ABC의 각 A의 외각의 이등분선과 BC의 연장선의 교점을 D라 하고
AD에 평행한 선분을 C에서 그어 AB와 만나는 점이 E라고 한다면...
각 FAD는 FEC와 같다.
각 CAD와 각 ACE는 서로 같다(엇각)
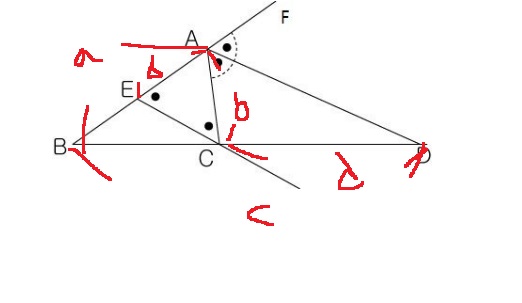
따라서 삼각형 AEC는 이등변삼각형이고 AE = AC
이 때 ABD와 BEC가 서로 닮음이므로...
a : a-b = c: c-d
계산하면 ac - bc = ac - ad
bc = ad
따라서 a:b = c:d
3. 연습문제
16485번: 작도하자! - ② (acmicpc.net)
16485번: 작도하자! - ②
첫째 줄에 c, b의 값이 사이에 공백을 한 개 두고 차례대로 주어진다. (c와 b의 값은 1,000,000,000 이하의 양의 정수이다.)
www.acmicpc.net
4. 풀이
내각의 이등분선 정리를 그대로 적용하면 된다

그림에서 내각의 이등분선 정리에 의해 c:b = BM:MC이고,
b * BM = c * MC이고, 그러므로 BM/MC = c/b
from sys import stdin
c,b = map(int,stdin.readline().split())
print(c/b)'기하학' 카테고리의 다른 글
| 삼각형의 내접원의 반지름과 방접원의 반지름의 관계식 (0) | 2023.03.10 |
|---|---|
| 컴퓨터로 원의 둘레를 추적하면서 개수를 세는 방법 (0) | 2023.03.10 |
| 스튜어트의 정리(Stewart's theorem) (0) | 2023.03.08 |
| 겹치는 직사각형의 넓이를 조건문 없이 구하기 (0) | 2023.03.06 |
| 네 점이 주어질때 정사각형인지 판단하는 방법 (0) | 2023.03.05 |

