1. 스튜어트의 정리
삼각형에서 다음이 성립한다
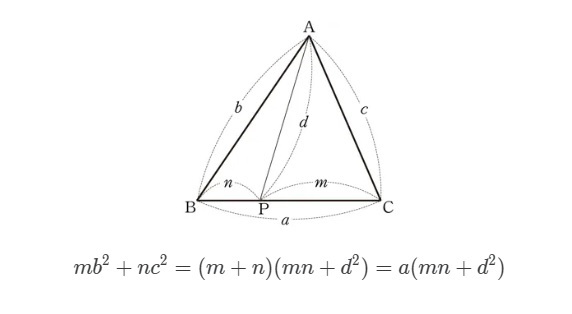
2. 증명
각 APC를 $\theta$라고 하자.

삼각형 APC에서 제2코사인법칙에 의해 $$c^{2} = d^{2} + m^{2} -2dm cos \theta$$
한편 삼각형 APB에서 제2코사인법칙에 의해, $$b^{2} = d^{2} + n^{2} - 2dn cos (\pi - \theta)$$
여기서 $cos (\pi - \theta) = -cos \theta$을 두번째 식에 대입하자
첫번째 식에 n을 곱하고 두번째 식에 m을 곱해서 더하면
$$mb^{2} + nc^{2} = md^{2} + mn^{2} + 2dmncos \theta + nd^{2} + nm^{2} - 2dmn cos \theta$$
우변을 계산하면,
$$mb^{2} + nc^{2} = md^{2} + mn^{2} + nd^{2} + nm^{2} = (m+n)(d^{2} + mn)$$
3. 연습문제
16488번: 피카츄가 낸 어려운 문제 (acmicpc.net)
16488번: 피카츄가 낸 어려운 문제
맨날 학교 칠판에 이등변삼각형을 그리고 노는 피카츄가 어느 날, 칠판에 변 AB와 변 AC의 길이가 모두 N인 이등변 삼각형을 그린 다음, 친구들에게 아래와 같은 문제를 냈다. 이등변삼각형 ABC에
www.acmicpc.net
4. 풀이
그림을 그려보면 대충 이렇다

$F(1) = d_{1}^{2} + m_{1}n_{1}$, ... , $F(k) = d_{k}^{2} + m_{k}n_{k}$
스튜어트의 정리에 의해, $$(d_{1}^{2} + m_{1}n_{1})(m_{1} + n_{1}) = m_{1}N^{2} + n_{1}N^{2} = N^{2}(m_{1}+n_{1})$$
따라서, $$(d_{1}^{2} + m_{1}n_{1}) = N^{2}$$
이는 모든 K = 1,2,3,...에 대해 성립한다
그러므로 $N^{2}$을 K배 하면 문제의 답이 될 것
from sys import stdin
n,k = map(int,stdin.readline().split())
print(k*(n**2))'기하학' 카테고리의 다른 글
| 컴퓨터로 원의 둘레를 추적하면서 개수를 세는 방법 (0) | 2023.03.10 |
|---|---|
| 삼각형의 내각의 이등분선과 외각의 이등분선 정리 (0) | 2023.03.09 |
| 겹치는 직사각형의 넓이를 조건문 없이 구하기 (0) | 2023.03.06 |
| 네 점이 주어질때 정사각형인지 판단하는 방법 (0) | 2023.03.05 |
| 사인법칙, 삼각형의 넓이, 코사인법칙, 외접원의 중심의 좌표 구하기 한번에 배우기 (0) | 2023.03.05 |

