1. 문제
6600번: 원의 둘레
입력은 여러 개의 테스트 케이스로 이루어져 있다. 각 테스트 케이스는 한 줄로 이루어져 있고, 실수 x1, y1, x2, y2, x3, y3이 주어진다. 세 점으로 만들 수 있는 원의 지름은 백만을 넘지 않는다.
www.acmicpc.net
2. 사인법칙을 이용한 풀이
다음 식을 사인법칙이라고 부른다

두 점 A,B의 길이를 구하고, 대각 A에 대한 sin값을 구한다.
sin값은 어떻게 구해야하나??
선택하지 않은 다른 점 C에 대하여 CA, CB 벡터를 구하고 두 벡터의 내적은 길이와 cos의 곱임을 이용해서 cos 값을 구할 수 있다.

그러면 cos과 sin의 제곱의 합은 1이므로 sin도 구할 수 있다
from sys import stdin
pi = 3.141592653589793
while 1:
try:
x1,y1,x2,y2,x3,y3 = map(float,stdin.readline().split())
#b,a의 길이
b = (x1-x3,y1-y3)
b2 = (b[0]**2 + b[1]**2)**(1/2)
a = (x2-x3,y2-y3)
a2 = (a[0]**2 + a[1]**2)**(1/2)
#b,a의 내적
ab = a[0]*b[0] + a[1]*b[1]
#내적의 성질
cos = ab/(a2*b2)
#cos과 sin의 관계
sin = (1-(cos**2))**(1/2)
c = ((x2-x1)**2 + (y2-y1)**2)**(1/2)
#sin법칙
print(f"{pi*c/sin:.2f}")
except:
break
사인 법칙 - 나무위키
사인법칙과 제2코사인법칙을 이용하여 아래 문제를 풀 수 있다. [풀이]세 변의 길이 비가 2k:3k:4k2k:3k:4k2k:3k:4k임을 알 수 있으므로, 제2코사인 법칙에 의해 cosC=(2k)2+(3k)2−(4k)22⋅2k⋅3k=−14 \cos{C}=
namu.wiki
3. 삼각형의 넓이를 이용한 풀이
삼각형의 넓이를 구하는 방법은 매우 많은데...
(총정리) 삼각형의 넓이 구하는 공식 (tistory.com)
(총정리) 삼각형의 넓이 구하는 공식
(총정리) 삼각형의 넓이 구하는 공식 이 포스팅은 삼각형의 넓이를 구하는 공식과 그 유도과정을 초,중,고 모든 학생을 망라하여 총정리한 글 입니다. 현업에서 수학을 많이 쓰는 사람으로서, 그
color-change.tistory.com
삼각형의 넓이는 기본적으로 밑변과 높이의 곱이다.
3-1) 두 변의 길이와 끼인각을 알 때
그런데 두 변 a,b의 길이와 사이의 끼인각 C를 알고 있을때, 높이 h는 다음과 같이..

$\frac{h}{b} = sinC$이므로 $h = bsinC$이다.
그러므로 삼각형의 넓이 $S = \frac{absinC}{2}$
3-2) 외접원의 반지름을 알 때
그런데 사인법칙에 의하면.. $\frac{c}{sinC} = 2R$이므로 $\frac{c}{2R} = sinC$
그러므로 외접원의 반지름을 알고 있을때, 삼각형의 넓이는 다음과 같이 구할 수도 있다.
$$S = \frac{abc}{4R}$$
3-3) 코사인법칙
한편 세변의 길이 a,b,c를 알고 있을때..
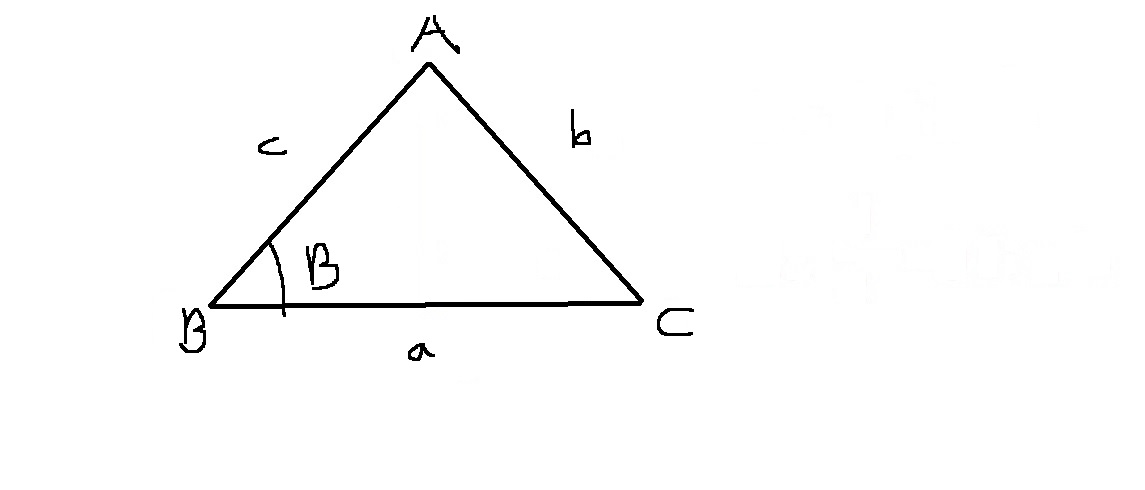
코사인 법칙이라고 불리는 다음 식이 성립한다

코사인 법칙 - 나무위키
비유클리드 기하학에서는 식의 형태가 완전히 달라진다. 제1 코사인 법칙cosa=cosbcosc+sinbsinccosAcosb=cosacosc+sinasinccosBcosc=cosacosb+sinasinbcosC\displaystyle \begin{aligne
namu.wiki
그러므로 cosB는 다음과 같이 구할 수 있다
$$cosB = \frac{c^{2} + a^{2} - b^{2}}{2ca}$$
sin과 cos의 제곱의 합은 1이다. 따라서.. sinB는 다음과 같다
$$sinB = \sqrt{1 - cosB ^{2}} = \sqrt{1 - (\frac{c^{2} + a^{2} - b^{2}}{2ca})^{2}}$$
3-4) 헤론의 공식
이걸 첫번째 구한 끼인각과 두 변의 길이를 알때 삼각형의 넓이를 구하는 공식에 대입한다면..
$$S = \frac{\sqrt{(ac)^{2} - \frac{(c^{2} + a^{2} - b^{2})^{2}}{4}}}{2}$$
식을 정리하면..
$$S = \sqrt{ \frac{( (a+b+c)(a-b+c) (b+a-c)(b-a+c) )}{16} }$$
이제 $s = \frac{(a+b+c)}{2}$라고 하자. 그러면 위 식은 다음과 같이 표현된다
$$S = \sqrt{s(s-a)(s-b)(s-c)}$$
세 점의 좌표를 알기 때문에 헤론의 공식으로 삼각형의 넓이를 구하고, 이를 abc/4R 공식과 비교하여
외접원의 반지름을 구한다면 원주를 구할 수 있다
from sys import stdin
pi = 3.141592653589793
while 1:
try:
x1,y1,x2,y2,x3,y3 = map(float,input().split())
a = ((x2-x1)**2 + (y2-y1)**2)**(1/2)
b = ((x3-x2)**2 + (y3-y2)**2)**(1/2)
c = ((x3-x1)**2 + (y3-y1)**2)**(1/2)
s = (a+b+c)/2
#헤론의 공식
S = (s*(s-a)*(s-b)*(s-c))**(1/2)
#외접원의 반지름
R = a*b*c/(4*S)
print(f"{2*pi*R:.2f}")
except:
break
4. 외접원의 중심의 좌표 구하기
세 점을 지나는 원의 중심의 좌표를 바로 구할 수는 없을까?
원의 중심의 좌표를 x,y라고 한다면 첫번째 점 (a,b)와 두번째 점 (c,d)까지 거리는 반지름으로 동일하다
$$(x-a)^{2} + (y-b)^{2} = (x-c)^{2} + (y-d)^{2}$$
식을 정리하면 다음 식을 얻는다
$$(2c-2a)x + (2d-2b)y = (c^{2} - a^{2}) + (d^{2} - b^{2})$$
마찬가지로 세번째 점 (e,f)까지 거리도 동일하므로...
$$(x-e)^{2} + (y-f)^{2} = (x-c)^{2} + (y-d)^{2}$$
이 식도 정리하면 다음 식을 얻는다
$$(2e-2c)x + (2f-2d)y = (e^{2} - c^{2}) + (f^{2} - d^{2})$$
2개의 방정식을 알고 있으므로 연립하면 x,y를 구할 수 있다
$$k_{1} = \frac{(c^{2} - a^{2}) + (d^{2} - b^{2})}{2}$$
$$k_{2} = \frac{(e^{2} - c^{2}) + (f^{2} - d^{2})}{2}$$
라고 표현하자.
$$(c-a)x + (d-b)y = k_{1}$$
$$(e-c)x + (f-d)y = k_{2}$$
(e-c)를 첫번째 곱하고 (c-a)를 두번째 곱해서 두 식을 빼면 y를 구할 수 있고
(f-d)를 첫번째 곱하고 (d-b)를 두번째 곱해서 두 식을 빼면 x를 구할 수 있다.
그러므로 x,y는 다음과 같다.
$$x = \frac{k_{1}(f-d) - k_{2}(d-b)}{(f-d)(c-a) - (d-b)(e-c)}$$
$$y = \frac{k_{1}(e-c) - k_{2}(c-a)}{(e-c)(d-b) - (c-a)(f-d)}$$
중심의 좌표를 알고 있으므로 (a,b)까지 거리가 반지름이 될 것이고 이를 이용해 원주를 구할 수 있다.
from sys import stdin
while 1:
try:
a,b,c,d,e,f = map(float,stdin.readline().split())
k1 = (c**2 - a**2 + d**2 - b**2)/2
k2 = (e**2 - c**2 + f**2 - d**2)/2
x = (k1*(f-d)-k2*(d-b))/((f-d)*(c-a) - (d-b)*(e-c))
y = (k1*(e-c)-k2*(c-a))/((e-c)*(d-b) - (c-a)*(f-d))
pi = 3.141592653589793
circumference = 2*pi*(((x-a)**2+(y-b)**2)**(1/2))
print(f"{circumference:.2f}")
except:
break
'기하학' 카테고리의 다른 글
| 겹치는 직사각형의 넓이를 조건문 없이 구하기 (0) | 2023.03.06 |
|---|---|
| 네 점이 주어질때 정사각형인지 판단하는 방법 (0) | 2023.03.05 |
| 평면 상의 다각형의 넓이 구하는 신발끈 공식 구현 (0) | 2023.03.05 |
| 외심과 내심의 직선거리를 구하는 방법 - 오일러의 삼각형 정리 (0) | 2023.02.21 |
| 넓이가 가장 넓은 평행사변형 찾기 (0) | 2023.02.21 |

