1. 문제
16480번: 외심과 내심은 사랑입니다 (acmicpc.net)
16480번: 외심과 내심은 사랑입니다
수진이는 외심과 내심 없이는 살 수 없다고 말할 정도로 외심과 내심을 사랑한다. 하지만, 갑자기 수진에게 어려운 일이 닥쳤다. 바로 평면에 있는 삼각형 ABC에서 외접원의 반지름의 길이 R이고,
www.acmicpc.net
2. 오일러의 삼각형 정리(Euler's triangle theorem)
삼각형의 외접원, 내접원, 방접원의 반지름이 각각 R, r, r'이라고 할때,
삼각형에서 외심과 내심 사이의 직선거리는 $\sqrt{R^{2} - 2Rr}$
외심과 방심사이 직선거리는 $\sqrt{R^{2} + 2Rr^{'}}$
근데 증명이 조금 까다롭던데 이걸 증명을 해봐야하는거냐 말아야하는거냐
외심과 내심 사이의 거리만 증명을 따라해보자
(증명)
2-1) 멘션의 정리
삼각형 ABC의 외접원이 O이고 내접원이 I이며, 직선 BI가 외접원과 만나는 점이 R이라고 하자.
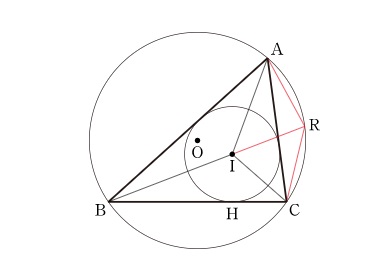
내심이 꼭짓점의 각을 이등분한다는 사실을 이용하면 다음과 같은 그림을 얻는다.
여기서 동일한 호에 대한 원주각은 서로 같으므로 CAR = CBR이고 ABR = ACR이다.
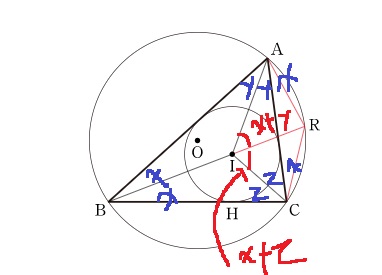
따라서 삼각형 AIR은 이등변삼각형이고 RIC도 이등변삼각형이다.
그러므로 AR = RI이고 RI = RC이므로, AR = RI = RC를 얻는다.

이제 그림과 같이 삼각형 ABC의 외심과 내심을 각각 O,I라고 하자.
B에서 내심 I를 지나 외접원과 만나는 점이 R일때, 직선 IO가 외접원과 만나는 점이 P,Q라고 하자.
PQ와 BR에 대한 방멱 정리(power theorem)에 의해..
PI * IQ = BI * IR이다.
구하고자 하는 OI = x라고 한다면... PO = R(외접원의 반지름)이라고 한다면..
PI = PO + OI = R+x
IQ = OQ - OI = R-x이다.
따라서, BI*IR = (R+x)(R-x)
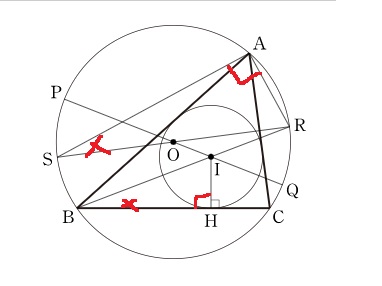
한편 지름의 원주각인 SAR = 90'이고 호 AR에 대한 원주각 ASR과 ABR은 서로 같다.
그런데 I는 내심이므로, ABR과 IBH가 서로 같다.
따라서 SAR과 BHI는 서로 닮았다.
그러므로 AR:SR = IH:BI
그런데, 멘션의 정리에 의하면 AR = IR이다. 따라서 IR:SR = IH:BI이고, SR * IH = IR * BI이다.
위에서 BI*IR = (R+x)(R-x)임을 증명했다.
SR = 2R이고 (외접원의 지름)
IH = r(내접원의 반지름)이다.
따라서, SR * IH = BI * IR = (R+x)(R-x) = 2Rr
그러므로 $$R^{2} - x^{2} = 2Rr$$
따라서, $$ x = \sqrt{R^{2} - 2Rr} $$
3. 풀이
위에서 증명한 공식에 그대로 대입하면 풀 수 있다.
R,r = map(int,input().split())
print(int(R**2 - 2*R*r))
참조
오일러 삼각형 정리 - 나무위키
Euler's triangle theorem 1765년 레온하르트 오일러(Leonhard Euler, 1707-1783)가 발견한 삼각형의 외심과 내심 혹은 외심과 방심 사이의 거리에 관한 공식이다. 한 삼각형의 외접원, 내접원, 방접원의 반지름
namu.wiki
'기하학' 카테고리의 다른 글
| 네 점이 주어질때 정사각형인지 판단하는 방법 (0) | 2023.03.05 |
|---|---|
| 사인법칙, 삼각형의 넓이, 코사인법칙, 외접원의 중심의 좌표 구하기 한번에 배우기 (0) | 2023.03.05 |
| 평면 상의 다각형의 넓이 구하는 신발끈 공식 구현 (0) | 2023.03.05 |
| 넓이가 가장 넓은 평행사변형 찾기 (0) | 2023.02.21 |
| 원을 두 현으로 분할할때 길이를 구하는 방법 - power theorem(방멱 정리) (0) | 2023.02.21 |

