1. 문제
1485번: 정사각형
첫째 줄에 테스트 케이스의 개수 T가 주어진다. 각 테스트 케이스는 네 줄로 이루어져 있으며, 점의 좌표가 한 줄에 하나씩 주어진다. 점의 좌표는 -100,000보다 크거나 같고, 100,000보다 작거나 같
www.acmicpc.net
2. 풀이
정사각형이 뭔지 상상해보면

첫번째 점과 두번째 점을 생각할 때 x좌표가 서로 다르면 안될 것 같고
x좌표가 서로 같다면... 세번째 점과 y좌표가 서로 같아야하고..
다르면 안될 것 같고
같다면 세번째 점과 네번째 점의 x좌표가 서로 같아야할 것 같고
다르면 안될 것 같고
같다면... 네번째 점과 두번째 점의 y좌표가 서로 같아야할 것 같고 다르면 안될 것 같고
만약 같다면 두 변의 길이가 서로 같은지 아닌지 검사해서 같으면 정사각형일 것 같다
from sys import stdin
t = int(stdin.readline())
for _ in range(t):
points = []
for _ in range(4):
x,y = map(int,stdin.readline().split())
points.append((x,y))
points.sort()
if points[0][0] != points[1][0]:
print(0)
else:
if points[0][1] != points[2][1]:
print(0)
else:
if points[3][0] != points[2][0]:
print(0)
else:
if points[3][1] != points[1][1]:
print(0)
else:
a = points[1][1] - points[0][1]
b = points[2][0] - points[0][0]
if a == b:
print(1)
else:
print(0)
근데 이렇게 하면 오답인데.. "네 점이 x좌표가 모두 다르더라도 정사각형일 수 있다"
다음과 같이 기울어져도 네 변의 길이가 서로 같고 모든 각이 직각이면 정사각형이잖아
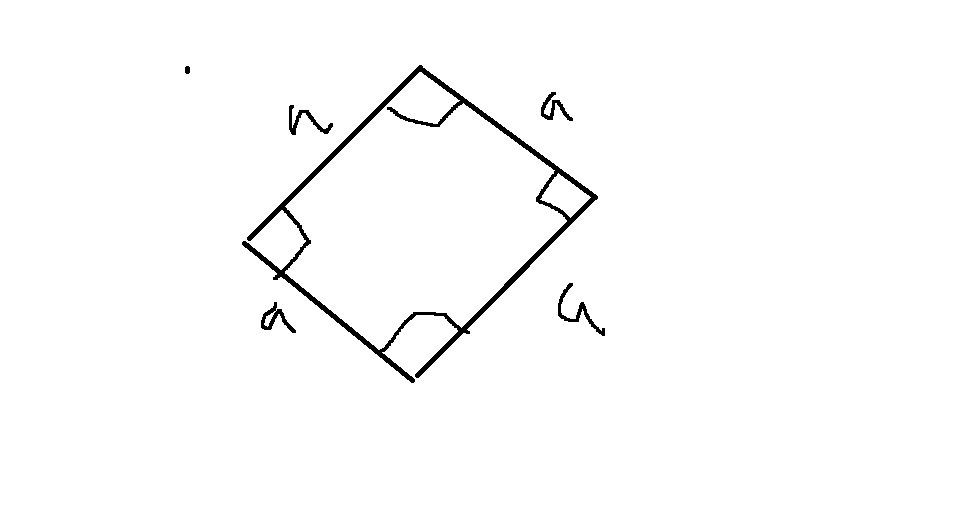
조금 다르게 생각해서 다음과 같이 접근해보자
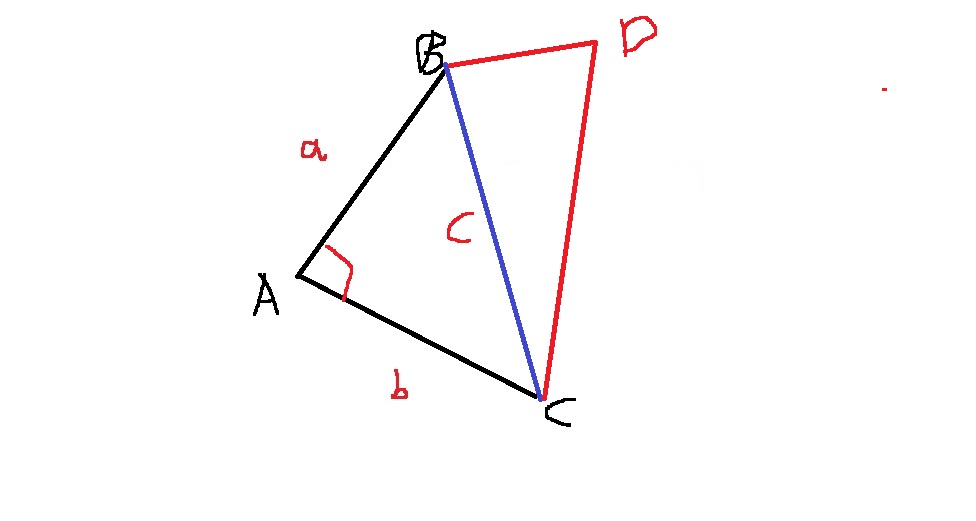
두 변의 길이를 구하고, 대각선의 길이를 구한 다음에
두 변의 길이가 서로 같으면서 두 변의 길이의 제곱의 합이 대각선의 길이의 제곱과 같다면.. 정사각형일 것이다

근데 주의할 점은 BC의 길이를 대각선의 길이로 정하면 당연히 오답이다
from sys import stdin
def distance(a,b):
return ((a[0]-b[0])**2 + (a[1]-b[1])**2)
t = int(stdin.readline())
for _ in range(t):
points = []
for _ in range(4):
x,y = map(int,stdin.readline().split())
points.append((x,y))
points.sort()
a = distance(points[0],points[1])
b = distance(points[0],points[2])
c = distance(points[0],points[3])
if a == b and a+b == c:
print(1)
else:
print(0)728x90
'기하학' 카테고리의 다른 글
| 스튜어트의 정리(Stewart's theorem) (0) | 2023.03.08 |
|---|---|
| 겹치는 직사각형의 넓이를 조건문 없이 구하기 (0) | 2023.03.06 |
| 사인법칙, 삼각형의 넓이, 코사인법칙, 외접원의 중심의 좌표 구하기 한번에 배우기 (0) | 2023.03.05 |
| 평면 상의 다각형의 넓이 구하는 신발끈 공식 구현 (0) | 2023.03.05 |
| 외심과 내심의 직선거리를 구하는 방법 - 오일러의 삼각형 정리 (0) | 2023.02.21 |

