https://gaussian37.github.io/math-la-cross-product/
벡터의 외적이란?
gaussian37's blog
gaussian37.github.io
https://cp-algorithms.com/geometry/basic-geometry.html#definition_1
Basic Geometry - Algorithms for Competitive Programming
Basic Geometry In this article we will consider basic operations on points in Euclidean space which maintains the foundation of the whole analytical geometry. We will consider for each point $\mathbf r$ the vector $\vec{\mathbf r}$ directed from $\mathbf 0
cp-algorithms.com
https://en.wikipedia.org/wiki/Cross_product
Cross product - Wikipedia
From Wikipedia, the free encyclopedia Mathematical operation on vectors in 3D space The cross product with respect to a right-handed coordinate system In mathematics, the cross product or vector product (occasionally directed area product, to emphasize its
en.wikipedia.org
1. 외적(cross product)
The cross product a × b is defined as a vector c that is perpendicular (orthogonal) to both a and b
두 벡터 a,b에 대하여 동시에 수직인 벡터 $c = a \times b$
The cross product of two vectors a and b is defined only in three-dimensional space and is denoted by a × b.
내적(inner product)은 모든 차원에서 정의되지만, 외적(cross product)은 오직 3차원에서만 정의된다.
2. 외적의 방향
3차원 공간 위에 두 벡터 a,b가 존재할때, 두 벡터에 동시에 수직인 벡터는 위로 향하는 벡터와 아래로 향하는 벡터가 있다

두 벡터 a,b가 주어질때, 외적의 방향은 오른손 법칙을 이용해 알아낼 수 있다
앞에 곱하는 a를 검지에, 뒤에 곱하는 b를 중지에 두고,
오른손의 엄지손가락이 가리키는 방향이 외적 $a \times b$의 방향

3. 외적을 구하는 방법
행렬식 표현으로 구하는게 가장 무난하다
a = (a1,a2,a3), b = (b1,b2,b3)라고 표현할 수 있을때,
$$a \times b = \begin{vmatrix}
1 & 1 & 1 \\
a_{1} & a_{2} & a_{3} \\
b_{1} & b_{2} & b_{3} \\
\end{vmatrix}$$
행렬식을 계산하는 방법을 기억해보면... 먼저 아무 행이나 하나 지정하고.. 1행이 (1,1,1)이니까 이를 지정하는게 가장 무난하다
먼저, 1행 1열의 원소 1을 지정하면, 행렬식에서 1행, 1열을 제거하고 남은 minor에 (1,1) 원소를 곱하고, $(-1)^{1+1}$을 곱해
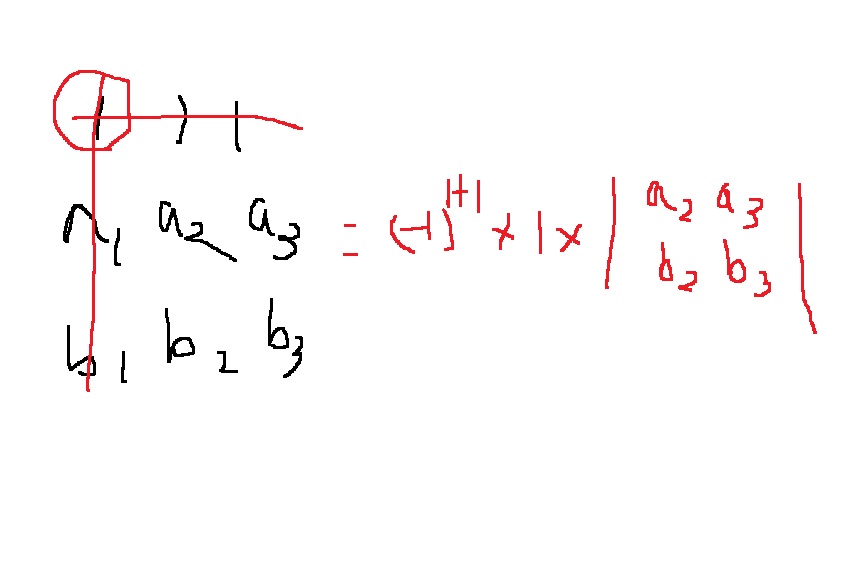
2*2 행렬식을 구하는 방법은 $$\begin{vmatrix}
a & b \\
c & d \\
\end{vmatrix} = ad-bc$$라는 것은 기본적으로 알고 있다
두번째 (1,2) 원소를 지정하고, 1행 2열을 제거한 minor를 곱하고, $(-1)^{1+2}$를 곱해서...

마지막 (1,3) 원소를 지정하고, 1행 3열을 제거한 minor를 곱한 다음, $(-1)^{1+3}$을 곱해주자..

파이썬으로 구현하면 다음과 같다.
def cross_product(a,b):
return (a[1]*b[2] - a[2]*b[1]) - (a[0]*b[2] - a[2]*b[0]) + (a[0]*b[1] - a[1]*b[0])
기억이 안난다면 위 행렬식 표현 그림을 기억하면서, 구하면 되겠지..
4. 반드시 알아야하는 기본 성질
증명은 모두 생략함
1) 두 벡터의 연산 순서를 교환하면, -1을 곱해줘야한다.
$$a \times b = - b \times a$$
2) 두 벡터의 외적이 영벡터이면, $a \times b = 0$이라면,
2-1) 두 벡터중 적어도 하나는 영벡터이다. $a = 0$이거나, $b = 0$이다.
2-2) 그런데, 둘 다 영벡터가 아니라면, 두 벡터는 서로 평행하다.
3) 두 벡터의 외적의 크기는, 두 벡터가 이루는 각 $\theta$에 대하여,
$$| a \times b | = | a | | b | sin \theta$$
기하학적으로, 두 벡터 a,b가 이루는 평행사변형의 넓이와 같다.

따라서, 외적의 크기의 절반이, 두 벡터가 이루는 삼각형의 면적과 같다.
신발끈 공식은 위의 원리에서 나왔다.
https://deepdata.tistory.com/733
평면 상의 다각형의 넓이 구하는 신발끈 공식 구현
1. 문제 2166번: 다각형의 면적 (acmicpc.net) 2166번: 다각형의 면적 첫째 줄에 N이 주어진다. 다음 N개의 줄에는 다각형을 이루는 순서대로 N개의 점의 x, y좌표가 주어진다. 좌표값은 절댓값이 100,000을
deepdata.tistory.com
5. 내적과 외적의 관계식
두 벡터 a,b가 이루는 각이 $\theta$라고 할 때,
1) 두 벡터의 내적 $a·b = |a||b|cos \theta$
2) 두 벡터의 외적 $|a \times b| = |a||b| sin \theta$
3) $(|a \times b|)^{2} = |a|^{2} |b|^{2} - (a · b)^{2}$
6. 2차원에서의 외적
벡터의 외적이 3차원에서만 정의된다고 했지만, 2차원 위의 두 점 a = (a1,a2), b = (b1,b2)의 외적은 어떻게 구할까?
이는 a = (a1,a2,0), b = (b1,b2,0)의 외적과 같다.
2차원 평면 위의 점 a,b는 z축 좌표를 0으로 고정시킨 3차원 위의 점과 같기 때문이다.
7. 세 벡터가 이루는 육면체의 부피
다음과 같은 육면체의 부피는 어떻게 구할 수 있을까

결론부터 말하면, $$V = | a · (b \times c) |$$
육면체의 부피는, 밑면의 넓이 base에 높이 h를 곱한 값이다.
밑면의 넓이 base는 $b \times c$의 크기가 된다.
높이 h는 벡터 a에 $cos \alpha$를 곱한 값으로 구할 수 있다.
두 벡터의 내적이, $|a · b| = |a| |b| cos \alpha$로 구할 수 있으므로,
$$V = |a| cos \alpha |b \times c| = |a| |b\times c| cos \alpha = |a · (b \times c)|$$
'기하학' 카테고리의 다른 글
| 모든 좌표 쌍의 맨해튼 거리의 합을 효율적으로 구하는 방법 (0) | 2023.08.24 |
|---|---|
| 기하학의 사칙연산인 CCW(Counter-ClockWise) 알고리즘 배우기 (0) | 2023.08.05 |
| 나비 정리(butterfly theorem) (0) | 2023.03.21 |
| 삼각형의 내접원의 반지름과 방접원의 반지름의 관계식 (0) | 2023.03.10 |
| 컴퓨터로 원의 둘레를 추적하면서 개수를 세는 방법 (0) | 2023.03.10 |

