CCW (Counter-ClockWise) - (1)
CCW (Counter-ClockWise) - (1) CCW 알고리즘은 수 계산에서의 사칙연산처럼, '기하 알고리즘'에서 가장 기본적인 알고리즘이다. 즉, 기하 알고리즘에서 매우 자주 이용된다는 뜻이다. 우선 이 게시글에서
rebro.kr
https://gaussian37.github.io/math-algorithm-ccw/
CCW(counter clockwise)
gaussian37's blog
gaussian37.github.io
https://snowfleur.tistory.com/98
[알고리즘] CCW(Counter Clock Wise)
알고리즘 개요 및 소개 CCW( Counter Clock Wise) 알고리즘은 3개의 점 A, B, C가 있을 때 이 점 3개를 이은 직선의 방향을 알고자 할 때 유용한 기하 알고리즘이다. 경우의 수는 총 3가지가 있으며 시계,
snowfleur.tistory.com
1. CCW(counter clockwise)
시계 반대방향이라는 뜻
평면 위에 존재하는 세 점 A,B,C의 위치 관계를 구하는 알고리즘이다.
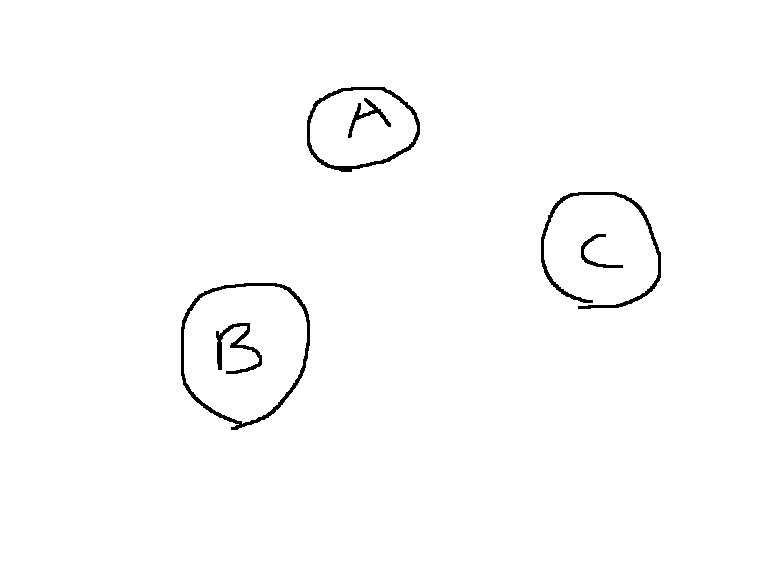
세 점 A,B,C의 위치관계는 A,B,C 순서대로 선분을 이을때, 다음과 같이 3가지 경우가 있다.
1) 시계 반대방향
2) 시계 방향
3) 일직선 위

2. 알고리즘
위의 그림과 같이 세 점 A,B,C가 주어질때, A,B,C를 선분으로 이을때, 어떤 방향을 이루는지 알고 싶다.
먼저 A를 기준으로 벡터 AB와 벡터 AC를 구한다.
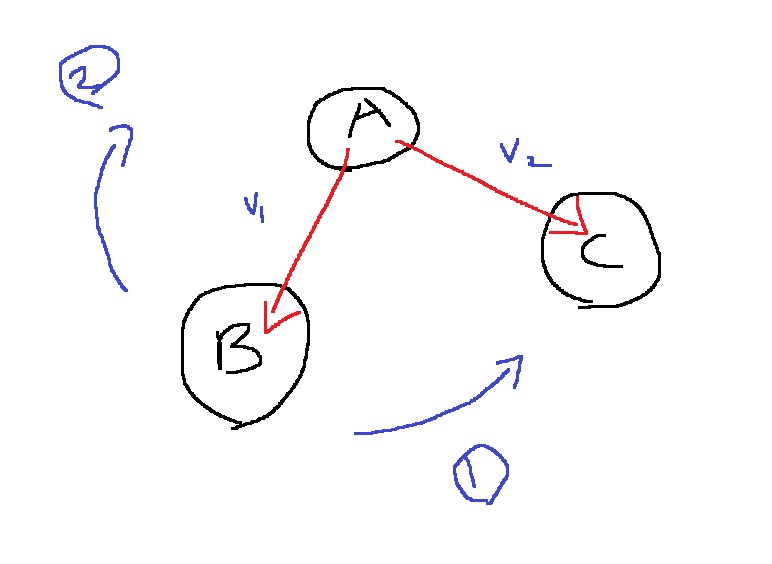
v1 = AB를 기준으로 v2를 향해 회전시킬때, 1번 방향으로 회전한다면 시계반대방향,
2번방향으로 회전한다면 시계방향이라는 뜻이다.
벡터의 외적을 이용하면, 어느방향으로 회전될지 알 수 있다.
https://deepdata.tistory.com/956
기하학 알고리즘의 기본 - 두 벡터의 외적(cross product)에 대하여
https://gaussian37.github.io/math-la-cross-product/ 벡터의 외적이란? gaussian37's blog gaussian37.github.io https://cp-algorithms.com/geometry/basic-geometry.html#definition_1 Basic Geometry - Algorithms for Competitive Programming Basic Geometry In
deepdata.tistory.com
벡터의 외적의 방향은 오른손 법칙을 이용하여 그 방향을 알 수 있는데,
$AB \times AC$를 구할때, 이 벡터의 방향은...
AB를 검지에 두고, AC를 중지에 두어서, 오른손으로 감싸면, 벡터의 외적은 위쪽 방향을 가리키며 1번방향(반시계)으로 회전
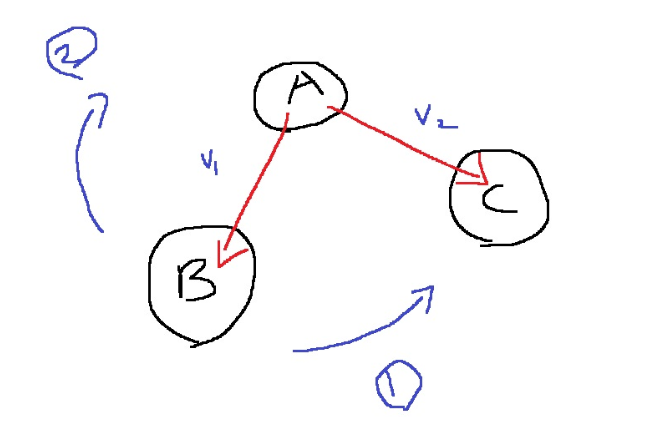
반대로 A,B,C가 다음과 같이 주어진다면...
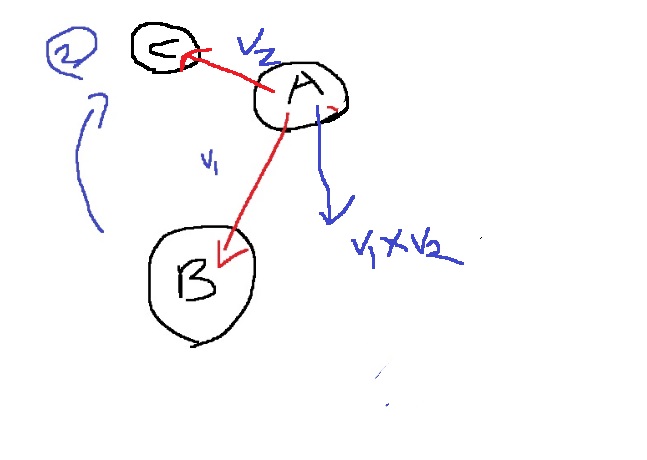
오른손으로 v1을 검지에 두고, v2를 중지에 두면 엄지가 아래로 가리키며, 오른손이 감싸는 방향이 2번방향(시계방향)이다.
두 벡터의 외적이 영벡터일때, 두 벡터가 서로 영벡터가 아니라면, 두 벡터는 서로 평행하다.
즉, $AB \times AC = 0$이라면, AB와 AC가 서로 평행하여, 일직선 위에 있다.
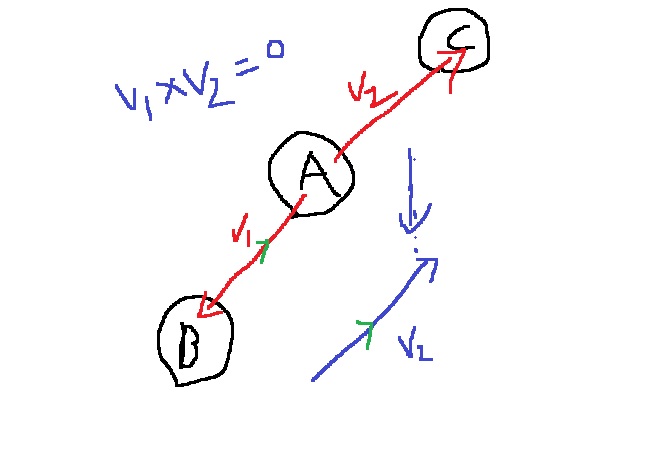
이 때, v1과 v2는 어떻게 구할 수 있을까?
A = (a1,a2,a3), B = (b1,b2,b3), C = (c1,c2,c3)일때, 이는 원점 O를 기준으로 만들어진 벡터이다.
즉, OA = (a1,a2,a3), OB = (b1,b2,b3), OC = (c1,c2,c3)이다.
여기서 AB = OB - OA = (b1 - a1, b2 - a2, b3 - a3)
AC = OC - OA = (c1 - a1, c2 - a2, c3 - a3)

그리고, 오른손 법칙에 의한, 위쪽 방향을 양수로 정의한다.
위 결과를 종합하면, A,B,C를 이은 선분이 어떤 관계를 이루는지 알기 위해 AB = OB - OA = v1, AC = OC - OA = v2를 구한다.
v1에서 v2로 시계 반대방향으로 회전하는 경우, 두 벡터 v1과 v2의 외적의 크기가 양수이다.
그래서 이 알고리즘의 이름이 counter clockwise(시계 반대방향)이라고 이름 붙었다.
v1에서 v2로 시계방향으로 회전하는 경우, 두 벡터 v1과 v2의 외적이 아래방향을 가리키고 크기가 음수이다.
v1와 v2가 평행한 경우, 두 벡터 v1과 v2의 외적의 크기가 0이다.
3. 연습문제
11758번: CCW
첫째 줄에 P1의 (x1, y1), 둘째 줄에 P2의 (x2, y2), 셋째 줄에 P3의 (x3, y3)가 주어진다. (-10,000 ≤ x1, y1, x2, y2, x3, y3 ≤ 10,000) 모든 좌표는 정수이다. P1, P2, P3의 좌표는 서로 다르다.
www.acmicpc.net
4. 풀이
위 알고리즘을 그대로 구현하면 정답
2차원 위의 점 A,B,C를 받기 때문에, AB, AC를 구할때 z축 좌표를 0으로 만들어야한다는 점에 유의
#A,B,C를 이은 선분이 어떤 관계를 이루는가
#두 벡터 a,b의 외적
def ccw(a,b):
return (a[1]*b[2] - a[2]*b[1]) - (a[0]*b[2] - a[2]*b[0]) + (a[0]*b[1] - a[1]*b[0])
#세 점 A,B,C의 좌표
x1,y1 = map(int,input().split()) #A
x2,y2 = map(int,input().split()) #B
x3,y3 = map(int,input().split()) #C
#2차원이면, z축 좌표를 0으로
a = [x2 - x1, y2 - y1, 0] #AB
b = [x3 - x1, y3 - y1, 0] #AC
x = ccw(a,b)
if x > 0: #A,B,C를 이은 선분이 반시계방향
print(1)
elif x < 0: #A,B,C를 이은 선분이 시계방향
print(-1)
else: #A,B,C를 이은 선분이 직선
print(0)
'기하학' 카테고리의 다른 글
| 모든 좌표까지 맨해튼 거리 합이 최소가 되는 위치를 구하는 방법 (0) | 2023.08.24 |
|---|---|
| 모든 좌표 쌍의 맨해튼 거리의 합을 효율적으로 구하는 방법 (0) | 2023.08.24 |
| 기하학 알고리즘의 기본 - 두 벡터의 외적(cross product)에 대하여 (0) | 2023.08.05 |
| 나비 정리(butterfly theorem) (0) | 2023.03.21 |
| 삼각형의 내접원의 반지름과 방접원의 반지름의 관계식 (0) | 2023.03.10 |

