두 벡터 사이의 거리와 각도

1. 두 벡터 사이의 거리

 

벡터의 뺄셈을 이용

 

그림1. 두 벡터 x,y사이 거리를 구하는 과정

 

두 벡터 $x$ , $y$의 거리는 두 벡터의 뺄셈 $x-y$의 norm과 같다

 

 

2. 두 벡터 사이의 각도

 

L2 norm 에서만 정의됨

 

 

2-1) n차원에서 정의한 the law of cosines

 

그림2. 코사인 법칙 기본 삼각형 세팅

 

위 그림에서 아래 등식이 성립하는데 코사인 법칙이라고 부른다.

 

그림3. 코사인법칙

 

참고로 우리나라만 제1,2코사인법칙을 나눈다

 

세계적으로는 위와 같은 등식을 코사인법칙이라 한다

 

 

 

2-2) 두 벡터의 내적(dot product)

 

대응하는 성분의 곱의 합

 

그림4. 두 벡터의 내적

 

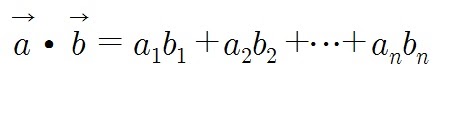
cosine을 이용하여 구할 수도 있다.

 

그림5. 두 벡터의 내적을 cos을 이용하여 구하는 과정

 

그림2에서 c의 값은 두 벡터 a와 b의 뺄셈 a-b의 norm으로 구할 수 있고

 

코사인법칙과 \[a\cdot b = \left\| a \right\|\left\| b \right\|cos\theta \]를 이용하여

 

우리는 다음과 같은 식을 얻는다.

 

 

따라서 두 벡터 사이의 각도에 대한 cosine값은 일반적으로

 

 

 

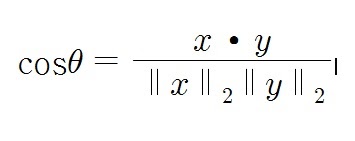
2-3) 두 벡터 사이의 각도

 

arccosine을 적용하여 두 벡터 사이의 각도를 구할 수 있다.

 

그림6. 두 벡터 x,y사이의 각도

 

numpy를 이용하여 구현하면

 

import numpy as np

def norm(x):
    
    return np.sqrt(np.sum(x*x))
    
def angle(x,y):
    
    v = np.inner(x,y)/(norm(x)*norm(y))
    
    theta = np.arccos(v)
    
    return theta
    
a = np.array([1,2])
b = np.array([3,4])

angle(a,b)
0.17985349979247847

 

 

3. 참고

 

https://en.wikipedia.org/wiki/Law_of_cosines#Using_vectors

Law of cosines - Wikipedia

 

 

https://blog.naver.com/PostView.nhn?isHttpsRedirect=true&blogId=mindo1103&logNo=90103350914 

벡터의 내적(Dot Product)