벡터의 norm은 벡터 사이 거리로 정의된다.
그런데 벡터 사이 거리를 어떻게 정의할까?
일반적으로 유클리드 거리를 생각하지만 사실 거리를 정의하는 방법은 다양하다
임의의 n차원에서 거리를 정의한다는 것이 중요하다.
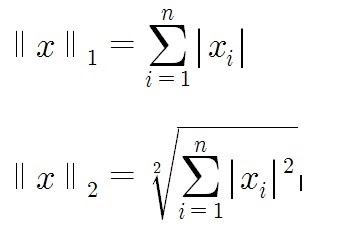
첫번째는 L1 norm, 두번째는 L2 norm이라고 부른다
1. L1 norm의 기하학적인 의미
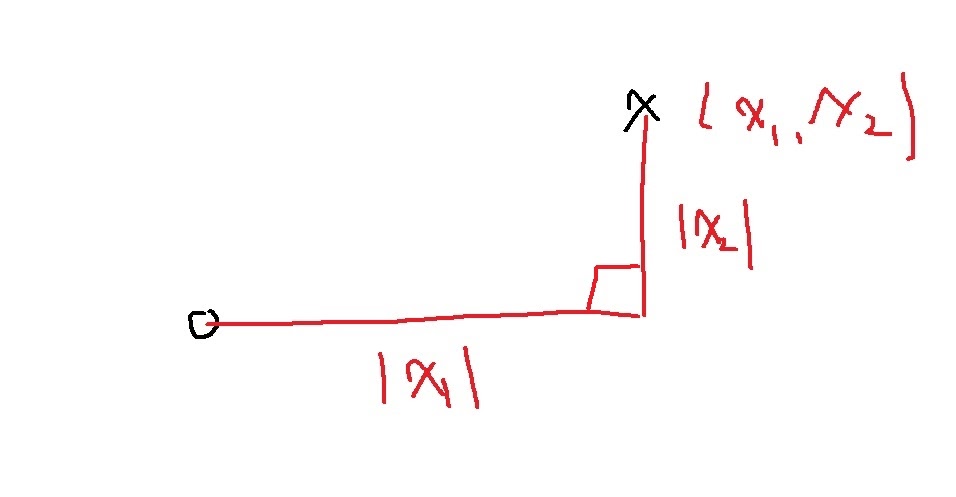
L1 norm이란 원점에서 x까지의 거리를 위 그림에서 빨간 선분의 총 길이로 정의하는 것이다.
2. L2 norm의 기하학적 의미

L2 norm은 x까지의 거리를 위와 같이 직선거리로 정의하는 것이다.
3. norm에 따른 원
원은 원점에서 거리가 r인 점의 집합이라는 사실로부터
3-1) L1 norm을 사용한 원
robust 방법, lasso 회귀 등에서 사용

3-2) L2 norm을 사용한 원
Laplace 근사나 Ridge 회귀에서 사용함
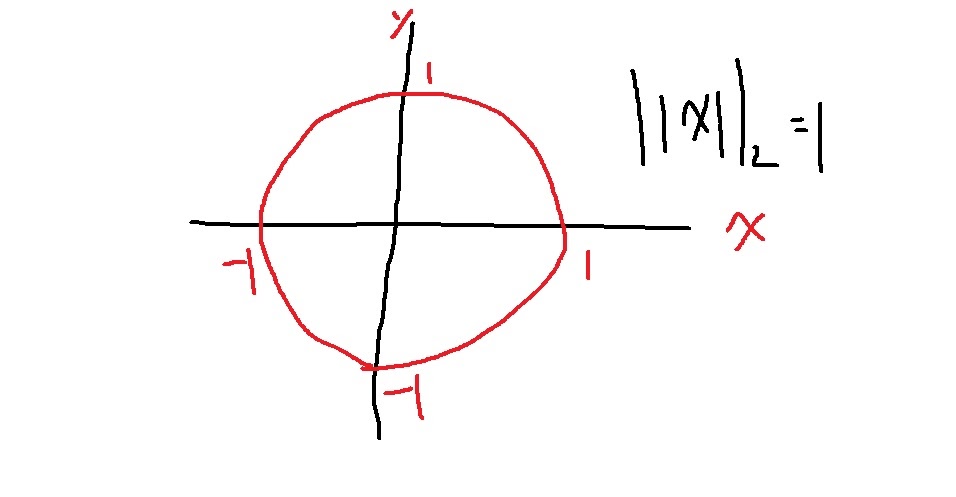
728x90
'선형대수학' 카테고리의 다른 글
| 벡터의 내적의 기하학적 의미 (0) | 2022.01.07 |
|---|---|
| 두 벡터 사이의 거리와 각도 (0) | 2022.01.06 |
| 벡터(vector)의 정의와 기본 연산 (0) | 2021.12.25 |
| 선형대수학 기본 용어 -상급자편 5- (0) | 2021.11.17 |
| 선형대수학 기본 용어 -상급자편 4- (0) | 2021.11.16 |

