행렬의 기하학적 의미

1. 행렬의 정의

 

벡터를 원소로 가지는 2차원 배열이다.

 

$n \times m$행렬 $X$는 다음과 같이 간단하게 나타낼 수 있다.

 

$$X= \left ( x_{ij} \right )$$

 

여기서 $i$는 행 인덱스, $j$는 열 인덱스

 

$x_{ij}$는 행렬 $X$의 $i$번째 행의 $j$번째 열에 있는 원소

 

 

2. 행렬의 분할

 

그림1. n*m행렬 X

 

그림2. 행렬의 분할

 

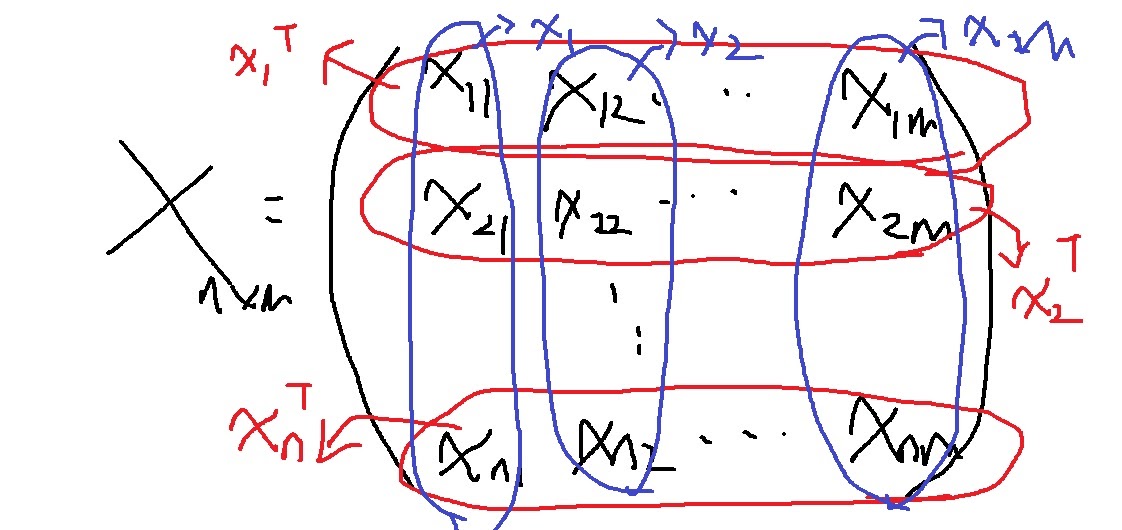
$i$번째 행을 기준으로 (빨간색 부분)

 

 

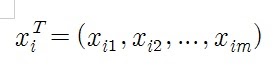
행벡터 분할하여 $n \times 1$행렬처럼 다룰 수도 있게 된다

 

그림3. 행벡터에 의해 분할된 행렬

 

행렬의 $j$열을 기준으로

 

 

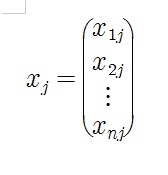
열벡터 분할하여 $1 \times m$ 행렬처럼 다룰 수 있게 된다

 

그림4. 열벡터에 의해 분할된 행렬

 

 

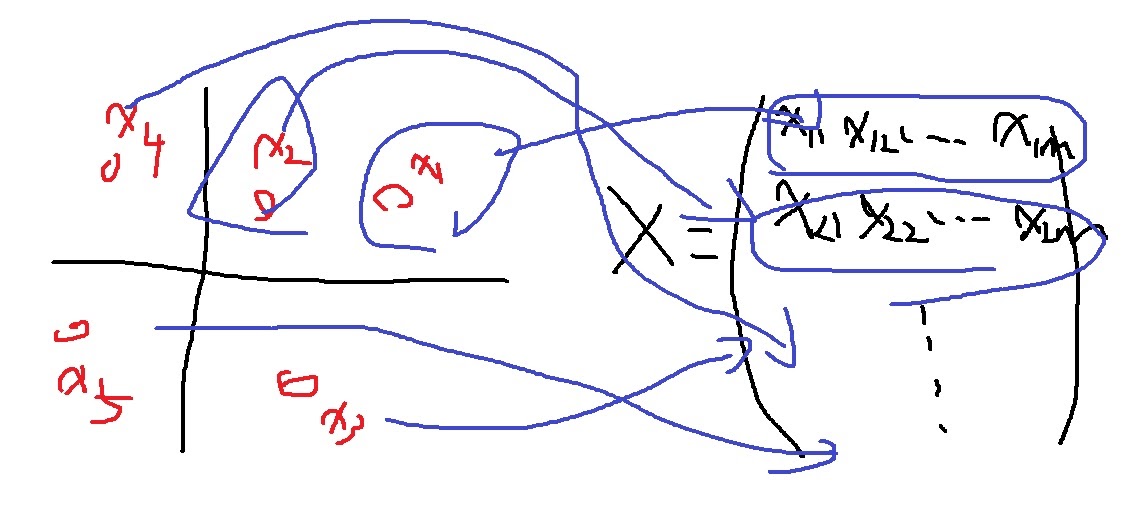
3. 행렬의 기하학적 의미

 

 

벡터가 공간 상 하나의 데이터를 나타낸다면, 행렬은 공간 상 여러개의 데이터를 하나로 묶어서 표현한 것이다

 

그림5. 행렬의 기하학적 의미