1. 기본적인 $O(n^{2})$ 알고리즘
기본 알고리즘을 다시 한번 생각해보자.
수열 s를 처음부터 순회하면서, i번째 원소를 읽었을때, 0~i번째 원소까지 최장 증가 부분수열의 길이는...
i보다 작은 인덱스 j에 대하여, dp배열의 0~j까지 모두 순회해서, j번째 숫자가 i번째 숫자보다 작다면, 그러한 j번째 숫자가 만드는 최장 증가 부분수열에 i번째 숫자를 포함시키면 된다
이렇게 찾은 최장증가부분수열의 길이들의 최댓값이 i번째 원소가 들어가는 최장 증가 부분수열의 길이였다
다익스트라 알고리즘에서 최단거리를 역추적하듯이 생각해보면 아주 심플하다
역추적을 위한 배열 p를 생각해서 현재 i번째 원소에 대한 dp값이 1이라면.. 최장 길이가 1이라는 뜻이니까
자기 자신이 최장 증가 수열의 시작점이니 p배열에는 -1을 저장하자(-1은 나올수없다고 가정)
그러다가 i번째 원소를 읽었는데 dp가 증가해서 2가 되었다
그러면 현재 p[i]에는 max(dp[j])가 되었던 s[j]를 저장하면 될 것이다
즉, 최장 증가 부분수열은.. ...., s[j], s[i]가 된다는 뜻이다
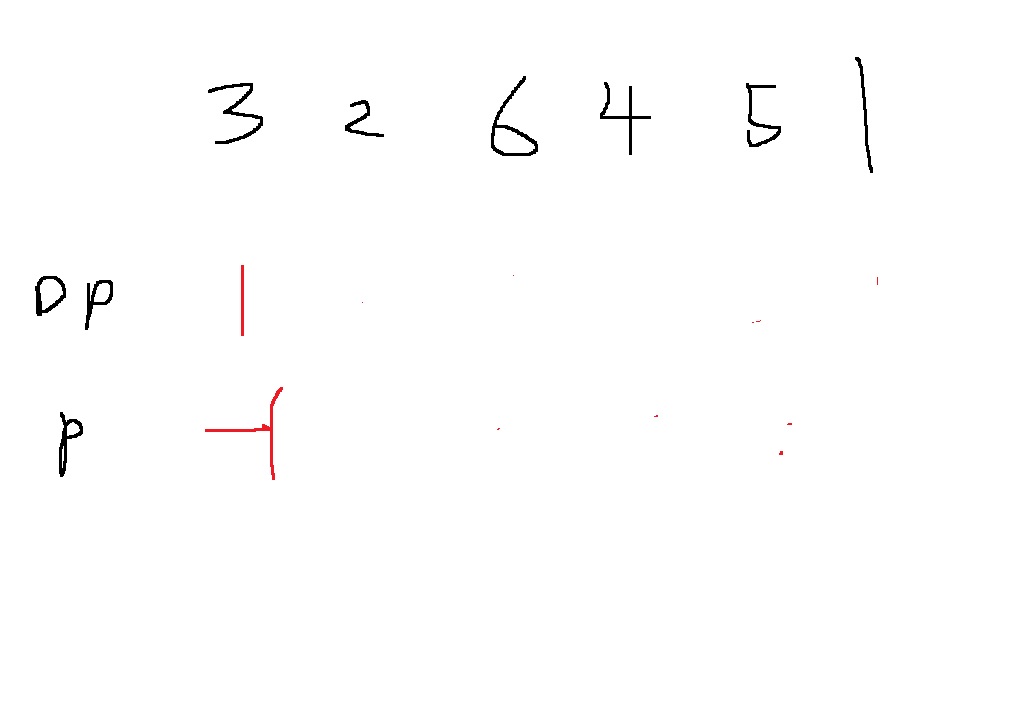
말로만 쓰면 무슨 말인지 모르겠으니 예시를 들어 생각해보자
3,2,6,4,5,1의 최장 증가 부분수열을 찾고자 한다.
먼저 3을 읽었을때, 최장 증가 부분수열의 길이는 1이므로 3이 부분수열의 시작점이라는 뜻에서 p배열에 -1을 저장

다음 2를 읽었을때, 2 이전의 숫자 중에서 2보다 작은 숫자는 존재하지 않는다
따라서 dp에는 1을 저장하고, 이는 2가 부분수열의 시작점이라는 뜻이다
따라서 p배열에 -1을 저장하자
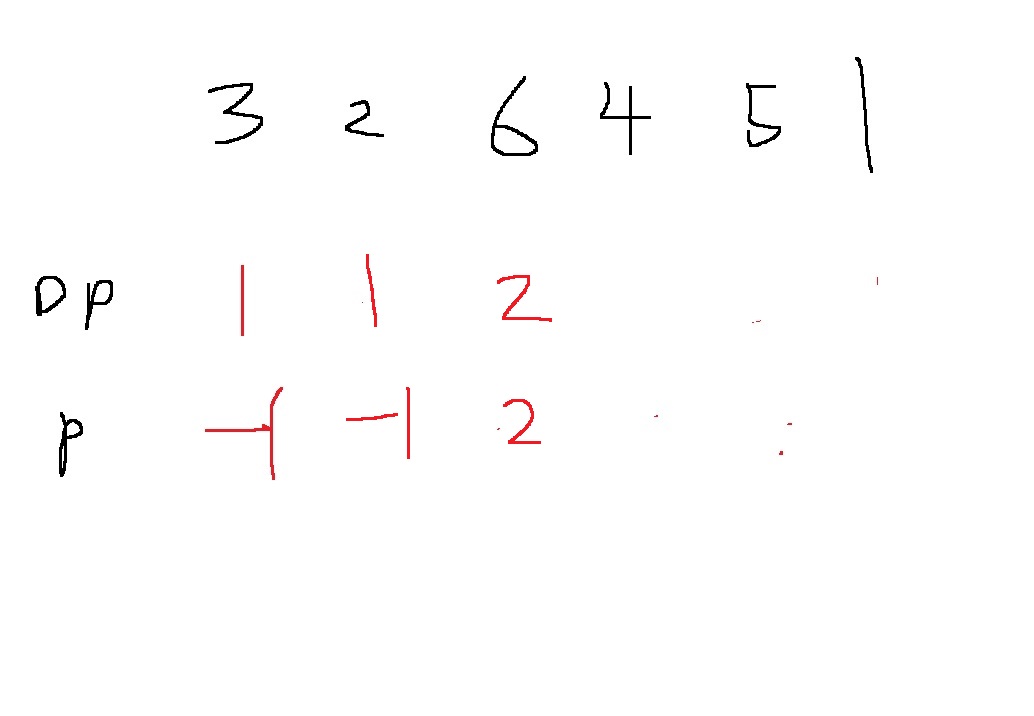
다음 6을 읽었을때, 6 이전의 숫자 중에서 6보다 작은 숫자들은 2,3이다.
2,3에서 dp값이 각각 1이므로, 최댓값은 1이고 6을 포함시키면 최장 증가 부분수열의 길이는 2이다
6 이전에 나온 숫자 2를 (3도 상관은 없을듯) p배열에 저장하자
만약 3,2,6까지 읽었을때, 최장 증가 부분수열은..?
dp의 max가 되는 위치를 찾는다
max가 되는 위치에서 p배열의 값을 찾는다.
해당 값을 인덱스로 하는 p배열의 값을 찾아나간다.
p배열의 값이 -1이 될때까지 반복한다
그러면 2,6이 최장 증가 부분수열이다. 계속 읽어보면..

위와 같이 채워나갈 수 있다. max(dp)가 최장 증가 부분수열의 길이이다.
그 위치의 숫자는 5이다
5부터 시작해서 p를 타고 나가 -1이 될때까지 반복해서 찾아나가면..
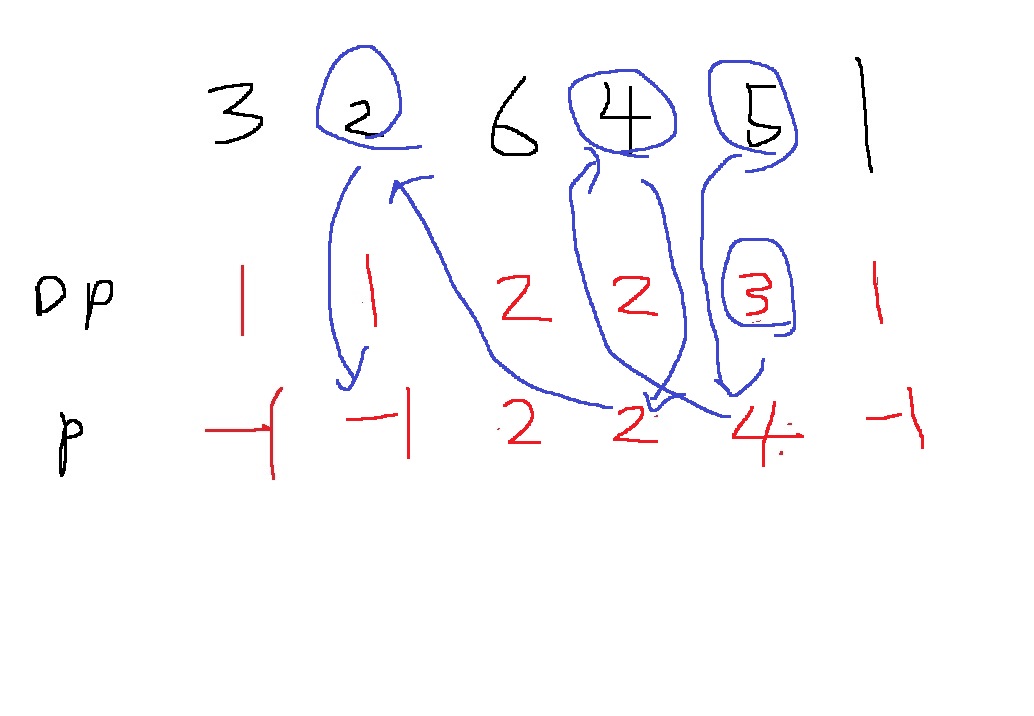
따라서 2,4,5가 최장 증가 부분수열이다.
2. 구현 예시
위 알고리즘 그대로 구현하면 되겠다.
근데 구현하고 보니까 (s[j],j])를 저장할게 아니라 j만 저장해놔도 되는거 아니여?
#다이나믹 프로그래밍으로 최장 증가 부분수열 찾기
s = [3,2,6,4,5,1]
n = len(s)
dp = [0] * n ##현재 위치의 최장 증가부분수열의 길이를 저장
#-1은 없다고 가정
p = [(-1,-1)] * n ##최장증가부분수열에서 해당 위치 이전에 나타날 수 있는 수
for i in range(n):
dp[i] = 1 #시작은 모두 1로 채우고..
for j in range(i):
#s[i]보다 작은 s[j]를 찾고..
if s[j] < s[i]:
#그러면 dp[i]는... dp[j]+1중에서 최댓값이.. s[i]가 포함된 최장 증가부분수열의 길이
if dp[i] < 1 + dp[j]:
dp[i] = 1+dp[j]
p[i] = (s[j],j) #현재 i번 이전에 나올 수 있는 j번 원소와 추적이 쉽게 인덱스도 같이 저장
###역추적
##max값이 되는 index를 찾는다
max_ind = 0
for i in range(n):
if dp[max_ind] < dp[i]:
max_ind = i
lis_list = [s[max_ind]]
#역추적해서 -1이 나올때까지 반복
while 1:
element,max_ind = p[max_ind] #원소와 해당 원소의 s배열에서의 위치
if element == -1: #원소가 -1이라면 해당 위치가 마지막이라는 뜻
break
lis_list.append(element)
print(lis_list[::-1])
"""
[3,4,5]
"""
3. 이분 탐색을 이용한 O(nlogn)알고리즘
이분 탐색을 이용해서 가장 긴 증가 부분수열을 구하는 알고리즘을 다시 한번 생각해보자.
어떤 배열 C를 하나 만들어서, 수열 리스트를 순회할때, 해당 숫자보다 크거나 같은 가장 작은 위치를 찾아서
배열 C안에서 그 위치에 숫자를 넣었는데
역추적을 위한 배열 P를 하나 만들어서, 이 P에는 수열의 각 원소가 C에 들어갈때, 어느 위치에 들어가는지를 저장한다
[Algorithm] LIS 알고리즘 (최장증가수열 알고리즘) (tistory.com)
[Algorithm] LIS 알고리즘 (최장증가수열 알고리즘)
LIS 알고리즘이란? LIS 알고리즘 (Longest Increasing Subsequence Algorithm) 은 최장증가수열 알고리즘으로 증가하는 원소들의 가장 긴 부분집합을 찾는 알고리즘이다. 풀이 1. DP로 풀기 시간 복잡도 O(N^2) 이
gom20.tistory.com
예시로 8,2,4,3,6,11,7,10,14,5에서 가장 긴 증가 부분 수열을 하나 찾아보자.
수열을 순회하면서, C배열과 P배열에 채워넣는다
C배열은 현재 숫자보다 크거나 같은 가장 최소의 위치에 집어넣고
P배열은 C배열의 어느 위치에 해당 숫자가 들어갔는지 저장한다

다음 2는 현재 C의 첫번째 8이 2보다 크거나 같은 가장 작은 위치이므로,,,

다음 4는?? 현재 이것보다 크거나 같은 숫자는 찾을 수 없으므로 C에 새로 삽입

현재 8,2,4까지 최장 증가 부분수열은.. 일단 C배열의 길이가 2이므로 가장 마지막에 들어간 인덱스는 1일것이다
P배열을 뒤에서부터 읽어서 값이 1인 숫자를 찾는다 >> 4
다음 1보다 작은 값인 0인 숫자를 찾는다 >> 2
따라서, 2,4가 최장 증가 부분수열
계속 3부터 읽어보면
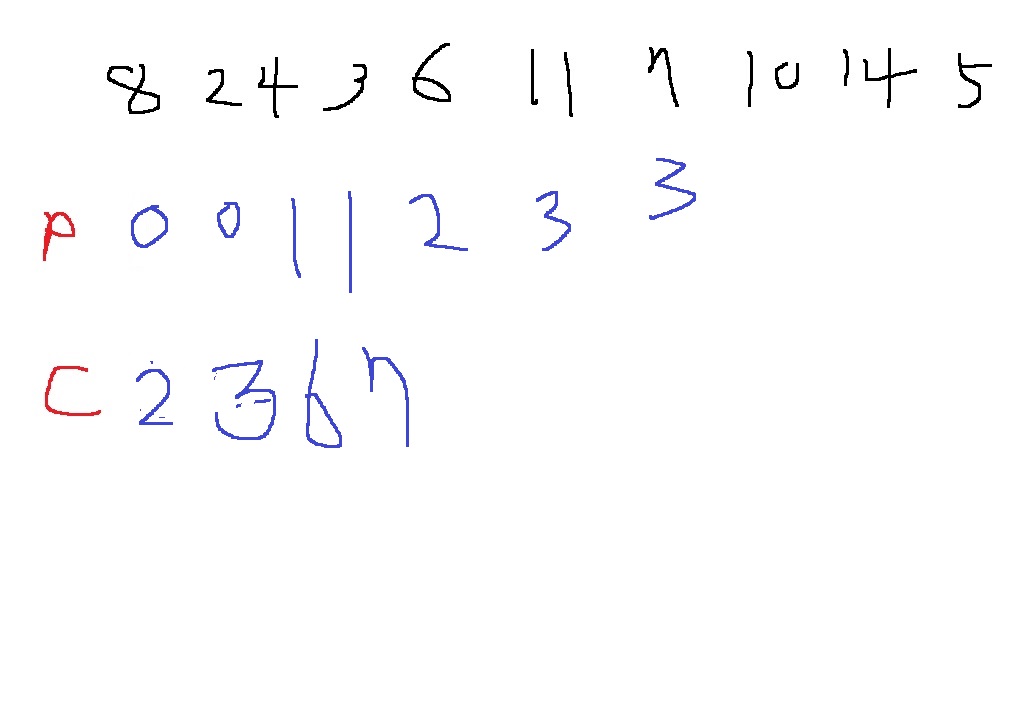
현재 C배열의 길이가 4이므로, 가장 마지막에 들어간 숫자의 값은 3일 것이다
P배열을 뒤에서부터 읽어서 가장 먼저 3인 숫자를 찾는다 >> 7
다음 가장 먼저 2인 숫자를 찾는다 >> 6
다음 가장 먼저 1인 숫자를 찾는다 >> 3
다음 가장 먼저 0인 숫자를 찾는다 >>2
따라서 최장 증가 부분수열은 2,3,6,7
이게 나중에 나오면 c배열을 덮어씌우잖아..
그래서 뒤에서부터 읽을때 가장 먼저 나온 값을 읽는거야
아무튼 계속 읽어보면..
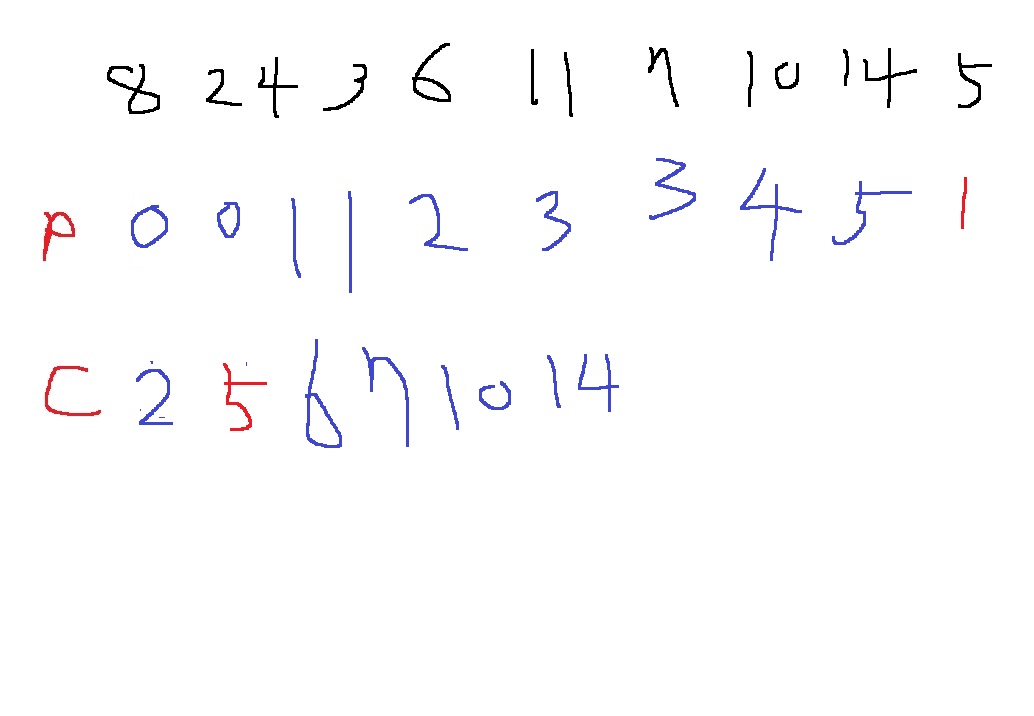
일단 c배열의 완성된 2,5,6,7,10,14는 증가하는 수열이긴 하지만, 원래 수열의 부분 수열은 아니다
아무튼 현재 c배열의 길이는 6이므로, 가장 마지막에 들어간 숫자의 p배열의 값은 5이다
p배열을 뒤에서부터 읽어서 가장 먼저 5가 나오는 숫자는 >> 14
다음 가장 먼저 4가 나오는 숫자는 >> 10
다음 가장 먼저 3이 나오는 숫자는 >> 7
다음 가장 먼저 2가 나오는 숫자는 >> 6
다음 가장 먼저 1이 나오는 숫자는 >> 3
다음 가장 먼저 0이 나오는 숫자는 >> 2
그러므로 최장 증가 부분수열은 2,3,6,7,10,14로 구할 수 있다
4. 구현 예시
위 알고리즘 그대로 구현하면 되겠다
핵심은 c배열에 숫자를 넣을때, 해당 숫자가 어느 위치에 들어가는지 정보를 저장하는 p배열을 만들고
역추적할때, p배열을 거꾸로 순회하는데
값이 LIS의 길이-1부터 0까지, 처음으로 나오는 값마다 해당 위치에 대응하는 숫자를 수열에서 찾아서 부분수열을 역추적 하면 되겠다
#이진 탐색으로 최장 증가 부분수열 역추적하기
##배열에서 읽어들인 숫자보다 크거나 같은, 최초의 위치를 찾는다
def lower_bound(array,target,start,end):
while start < end:
mid = (start+end)//2
if array[mid] >= target:
end = mid
else:
start = mid + 1
return end
s = [8,2,4,3,6,11,7,10,14,5]
n = len(s)
c = [1000000000000000000000000000000000]*n #매우 큰 값으로 c배열 초기화
p = [0]*n #c배열에 들어간 원소의 위치를 저장할 배열
LIS = 0 #현재 가장 긴 증가 부분수열의 길이
for i in range(n):
##num보다 크거나 같은 값 중에서 가장 작은 위치를 찾는다
loc = lower_bound(c,s[i],0,n)
#찾은 위치가 현재 가장 긴 증가 부분수열의 길이와 같다
if loc == LIS:
c[LIS] = s[i] ##그 위치에 숫자를 넣고
p[i] = LIS #i번째 숫자가 c배열에 들어간 위치를 저장
LIS += 1
else: #찾은 위치가 현재 가장 긴 증가 부분수열의 길이와 다르다면..?
c[loc] = s[i] #그냥 그 위치에 넣고,
p[i] = loc #p배열에도 그 숫자의 위치를 넣어준다.
##역추적
lis_list = [0]*LIS
target = LIS-1
for i in range(n-1,-1,-1): #p배열을 뒤에서부터 읽어들인다..
if p[i] == target:
lis_list[target] = s[i]
target -= 1
if target == -1:
break
print(lis_list)
"""
[2, 3, 6, 7, 10, 14]
"""
'알고리즘 > 다이나믹 프로그래밍' 카테고리의 다른 글
| dictionary와 재귀를 이용한 다이나믹 프로그래밍 기본 테크닉 배우기1 (0) | 2022.11.07 |
|---|---|
| 다이나믹 프로그래밍 - 2차원 배열 목적지까지 이동하는 방법의 수를 구하는 방법(파이프 옮기기) (0) | 2022.10.27 |
| 다이나믹 프로그래밍의 기본이 되는 동전 거스름돈 문제 해법 배우기 (0) | 2022.10.22 |
| 다이나믹 프로그래밍 - 최장 증가 수열(LIS)을 찾는 알고리즘 배우기 (0) | 2022.10.20 |
| 배낭(Knapsack) 문제, 다이나믹 프로그래밍 해법 배우기 (0) | 2022.10.19 |

