1. 문제
사용할 수 있는 동전이 1원,4원,6원이 있다. 거스름돈 8원을 내주기 위해 사용할 수 있는 최소 동전의 개수는?
그리디 방법으로 접근하면, 가장 큰것부터 내주면 최소라고 생각할 수 있으니까, 6원, 1원, 1원
그러나 실제 최적해는 4원, 4원으로 2개이다
그리디 방법이 항상 최적해를 보장해주지 않아서, 다른 방법으로 문제를 해결할 필요가 있다
- 완전 검색(백트래킹 이용가능)
- 다이나믹 프로그래밍
2. 재귀 알고리즘
3가지 동전 각각 선택하면 작은 부분문제가 생긴다
1원짜리 동전을 선택하면 >> 7원에 대한 최적해 + 1원 1개 >> 7원에 대한 최적해는 1원,4원,6원으로 다시 나눌 수 있음
4원짜리 동전을 선택하면 >> 4원에 대한 최적해 + 4원 1개
6원짜리 동전을 선택하면 >> 2원에 대한 최적해 + 6원 1개
8원에 대한 최적해는, 위 3가지 경우에서 최솟값을 선택

실제 문제 해결하는 상태공간 트리
단순하게 탐색하면 위와 같이 중복으로 해결해야하는 문제들이 너무 많이 생김
그래서 이미 해결한 문제는 메모이제이션을 이용해 정답을 저장해놓으면 시간을 단축할 수 있음
3. 메모이제이션 적용한 재귀 알고리즘 구현 예시
#재귀함수 + 메모이제이션 해법
n = 3 ##사용 가능한 동전 개수
coin = [6,4,1] ##사용가능한 동전 종류
change = 8 ##목표 거스름돈
memo = [-1]*(change+1) #이미 구한 부분 문제의 최적해를 저장하는 배열
memo[0] = 0 #0원은 0개.
INF = 100000000000000000000000 ##매우 큰 수
def coinchange(change):
##주어진 거스름돈에 대하여, 이미 정답을 구한 문제라면..
if memo[change] != -1:
return memo[change] ##바로 정답을 내놓는다
else: #아직 해를 구하지 않았다면..
min = INF
for i in range(n): #동전 종류만큼 각각 하나씩을 선택해봄
if change - coin[i] >= 0: ##동전 하나를 주고도 내줘야할 거스름돈이 존재한다면..
ret = coinchange(change-coin[i]) ## 그 남은 거스름돈을 내주기 위한 동전 개수 구하러
if min > ret:
min = ret ## 구한 동전 개수가 최솟값이라면 갱신하고
memo[change] = min + 1 ##남은 거스름돈 + 동전 하나 내준거
return memo[change]
print(coinchange(change))
"""
2
"""
4. 상향식 다이나믹 프로그래밍
거스름돈 금액을 0원부터 시작해서, 1원에 대한 최적해 > 2원에 대한 최적해 > 3원에 대한 최적해 > ... > 8원에 대한 최적해 > ... 까지 구해가는 방식
사용할 수 있는 동전 금액의 최솟값은 1원
그러므로 거스름돈 금액을 0원부터 시작해서 원하는 금액까지 1원씩 증가시켜서 모든 부분문제의 해를 구한다
0원은 0개를 내줘야하니까 dp[0] = 0
근데 사용 금액은 1원, 4원, 6원까지 있으니까, 시작이 0원일때 한번에 4원으로 갈수도 있고, 6원으로 갈 수도 있음

1원에 대한 문제를 해결할려면, 0원에 대한 부분 문제를 해결해야하고
4원에 대한 문제를 해결할려면, 0원에 대한 부분 문제를 해결해야하고,
6원에 대한 문제를 해결할려면, 0원에 대한 부분 문제를 해결해야함
확실히 0원을 해결하면, 1원에 대한 답을 알 수 있고..

2원에 대한 문제를 해결할려면 1원에 대한 부분 문제를 해결해야하고
5원에 대한 문제를 해결할려면 1원에 대한 부분 문제를 해결해야하고
7원에 대한 문제를 해결할려면 1원에 대한 부분 문제를 해결해야한다
0원을 해결했다면, 1원에 대한 답을 알수 있고, 1원에 대한 답을 알고 있다면.. 2원에 대한 답은 1원에 대한 부분 문제의 답으로부터 알 수 있다
즉 dp[2] = dp[1] + 1이고, dp[1] = dp[0] + 1
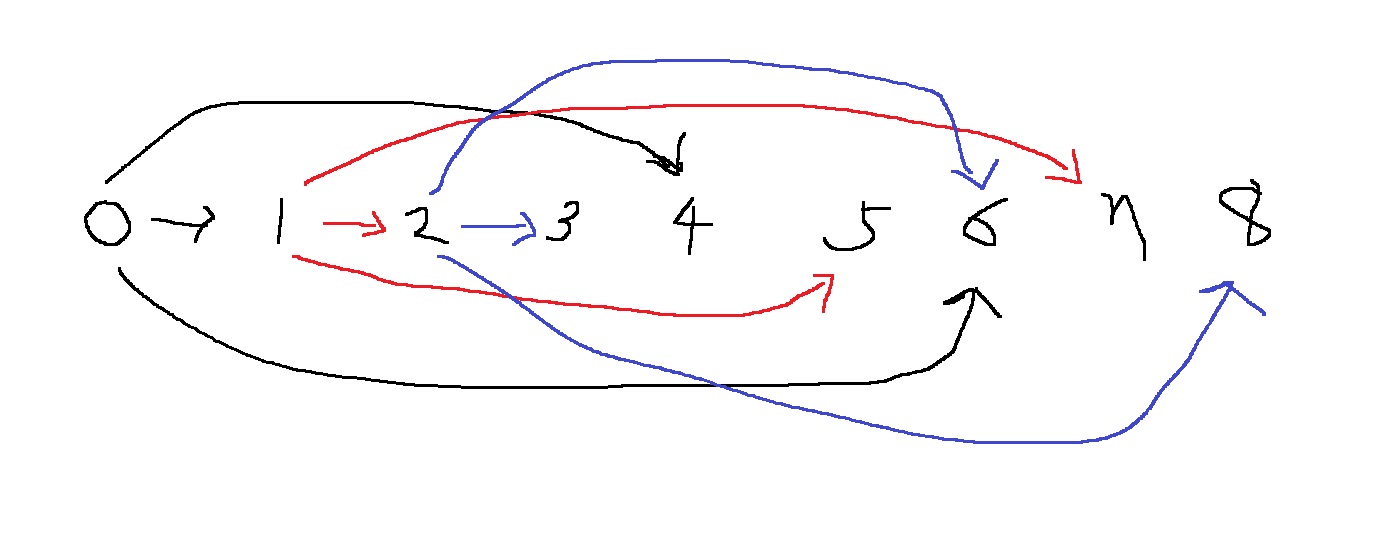
2원에 대한 답을 알았기 때문에, 3원에 대한 답도 알 수 있다
즉 dp[3] = dp[2]+1
6원에 대한 문제의 답은 0원에 대한 부분 문제의 답과, 2원에 대한 부분 문제의 답도 추가적으로 알아야한다
8원에 대한 문제의 답은 2원에 대한 부분 문제를 해결해야 한다

3원에 대한 문제를 해결했으므로, 4원에 대한 문제의 답은 3원에 대한 문제의 답과 0원에 대한 문제의 답으로부터 둘 중 최솟값으로 해결할 수 있다
즉 dp[4] = min(dp[3], dp[0]) +1
7원에 대한 문제의 답은 3원에 대한 부분문제의 답과 1원에 대한 부분문제의 답을 알아야한다
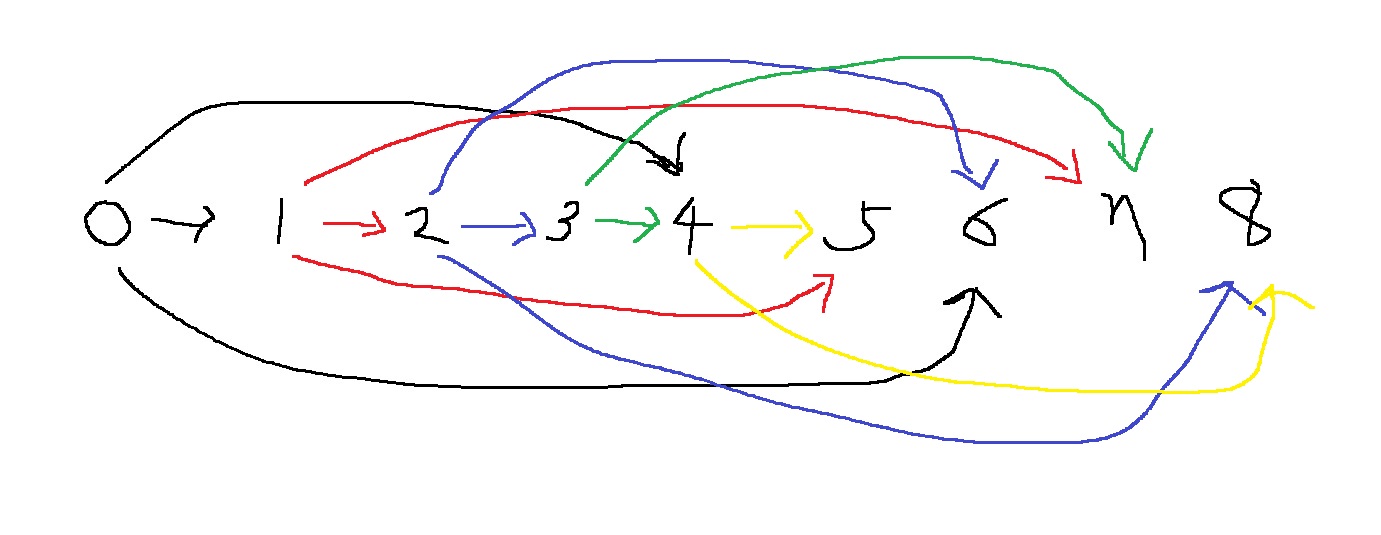
4원에 대한 문제의 답을 해결했으므로, 5원에 대한 문제의 답은 4원에 대한 부분문제의 답과 1원에 대한 부분문제의 답 중에서 최솟값으로 해결할 수 있다
즉 dp[5] = min(dp[4], dp[1]) +1
8원에 대한 문제의 답은 4원에 대한 부분문제의 답과 2원에 대한 부분문제의 답을 알아야한다

5원에 대한 문제까지 해결했으므로, 6원에 대한 문제의 답은 5원에 대한 부분문제의 답과 2원에 대한 부분문제의 답과 0원에 대한 부분문제의 답으로 해결할 수 있다
즉, dp[6] = min(dp[0], dp[2], dp[5]) +1
7원에 대한 문제의 답은 6원에 대한 부분문제의 답과 3원에 대한 부분문제의 답과 1원에 대한 부분문제의 답으로 해결할 수 있다
dp[7] = min(dp[1], dp[3], dp[6]) + 1
8원에 대한 문제의 답은 7원에 대한 부분문제의 답과 4원에 대한 부분문제의 답과 2원에 대한 부분문제의 답으로 해결할 수 있다
dp[8] = min(dp[2], dp[4], dp[7]) + 1
.....
그러므로 다음과 같은 결론을 얻는다
사용가능한 동전이 1,4,6원일때,
n원 거스름돈을 내주기 위해 사용해야할 최소 동전 개수는..
n이 6이상이면, dp[n] = min(dp[n-6], dp[n-4], dp[n-1]) + 1
n이 4이상 6미만이면, dp[n] = min(dp[n-4], dp[n-1]) + 1
n이 1이상 4미만이면, dp[n] = dp[n-1] + 1
아니 이거 완전 swea의 수영장 문제랑 똑같잖아??
5. 상향식 다이나믹 프로그래밍 구현 예시
사용가능한 동전 리스트를 정렬해주고.. 안해도 될려나?
정렬 할 필요는 없을듯
1원부터 목표 거스름돈까지 for문으로 순회를 시작.. i원이라하면.
사용가능한 동전 리스트를 순회해서.. c원이라하면
i원이 사용가능한 동전 값 이상이라면, 0원부터 시작했다면 i-c에 대한 답은 이미 dp배열에 존재해야하니까
그대로 가져오고, 최솟값을 계속 갱신해준다
그러면 i원에 대한 답은 min+1이고 그것을 dp[i]에 저장
change까지 모두 구했다면 dp[change]가 정답
n = 3 ##사용 가능한 동전 개수
coin = [6,4,1] ##사용가능한 동전 종류
change = 8 ##목표 거스름돈
# dp[i]는 i원을 내주기 위해 사용가능한 최소 동전 개수
dp = [0]*(change+1)
INF = 100000000000000000000 #매우 큰 수
for i in range(1,change+1): #1원부터 change원까지.. 내줘야할 동전 개수를 구한다
min = INF #최솟값 초기화
for c in coin:
if i >= c: #목표 값이 c원 이상이면..
ret = dp[i-c] #i-c에 대한 답은 이미 존재한다
if min > ret:
min = ret #구한 문제의 답이 최솟값이라면, 갱신해줌
dp[i] = min + 1 #모든 사용가능한 동전을 검사했다면 갱신
print(dp[change])
6. 연습문제
14916번: 거스름돈
첫째 줄에 거스름돈 액수 n(1 ≤ n ≤ 100,000)이 주어진다.
www.acmicpc.net
2원과 5원만을 가지고 거스름돈 n원을 내줄 수 있는 최소 동전 개수를 구하는 문제
7. 풀이
이번엔 거스름돈을 내줄 수 없는 경우도 생각해야된다
dp배열에 내줄 수 없는 경우는 -1로 채우자
그리고 구한 부분문제의 답이 -1이 아니라면, 최솟값을 갱신하고 -1이면 최솟값을 갱신하지 않는다
최솟값이 갱신되지 않았다면 -1로 dp배열을 채운다
from sys import stdin
n = int(stdin.readline())
coin = [2,5] #사용가능한 동전 종류
dp = [0]*(n+1)
dp[1] = -1 #내줄 수 없음
INF = 1000000000000000000000 #매우 큰 수
#0원,1원은 완성했으니까, 2원부터 n원까지
for i in range(2,n+1):
min = INF
#동전 종류를 순회
for c in coin:
#i원이 c원이상이라면, 거스름돈을 내줄 수 있다
#i-c에 대한 답은 이미 존재한다
if i >= c:
ret = dp[i-c]
#거스름돈 내주는 경우의 수가 -1이라면 내줄 수 없다는 뜻
#-1이 아니면서, 구한 경우의 수가 최솟값보다 작다면, 최솟값을 갱신해줌
if ret != -1 and min > ret:
min = ret
#최솟값이 갱신되지 않는다면, 거스름돈을 내줄 수 없다는 뜻
if min == INF:
dp[i] = -1
#최솟값이 갱신되었다면, 거스름돈을 내줄 수 있다는 뜻
else:
dp[i] = min + 1
#내줄 수 없다면 -1
#내줄 수 있다면 -1이 아니다
print(dp[n])'알고리즘 > 다이나믹 프로그래밍' 카테고리의 다른 글
| 다이나믹 프로그래밍 - 2차원 배열 목적지까지 이동하는 방법의 수를 구하는 방법(파이프 옮기기) (0) | 2022.10.27 |
|---|---|
| 가장 긴 증가 부분수열 실제 수열을 구하는 역추적 방법 (0) | 2022.10.26 |
| 다이나믹 프로그래밍 - 최장 증가 수열(LIS)을 찾는 알고리즘 배우기 (0) | 2022.10.20 |
| 배낭(Knapsack) 문제, 다이나믹 프로그래밍 해법 배우기 (0) | 2022.10.19 |
| 다이나믹 프로그래밍 연습하기 -수영장- (0) | 2022.10.08 |

