1. 문제
어떤 수열이 왼쪽에서 오른쪽으로 순서대로 나열된다.
3,2,6,4,5,1....
만약 이러한 나열된 순서를 유지하면서, 크기가 점진적으로 커지면서, 가장 긴 부분수열은 어떻게 찾을 수 있을까
이러한 부분수열은 연속적으로 고를 필요는 없다.
예를 들어 위 수열에서 3,4,5는 크기가 점점 커지는 부분수열이다.
2. 완전 검색
단순하게 완전 탐색을 수행해서 찾아낼 수도 있다
주어진 수열의 모든 부분집합을 구한다.
부분집합의 원소들이 증가하는 수열인지 검사한다.
증가하는 수열일때, 부분수열의 길이의 최댓값을 갱신한다.
당연히, 부분집합의 크기가 긴 것부터 조사하면, 처음으로 찾게되는 증가수열이 가장 긴 증가수열일 것이다.
#완전탐색으로 최장증가 부분수열 찾기
s = [3,2,6,4,5,1]
n = len(s)
#부분집합의 길이가 가장 긴것부터
for m in range(n,0,-1):
##부분집합을 찾는다
for i in range(1<<n):
partial = []
ans = False ##반복문 탈출을 위해 정의
for j in range(n):
if i & (1<<j):
partial.append(s[j])
##부분집합의 길이가 m이라면..
if len(partial) == m:
##증가 수열인지 판단
ans = True
for k in range(m-1):
if partial[k] > partial[k+1]: ##이전 원소가 한번이라도 더 크다면, 증가 수열이 아님
ans = False
break
if ans:
print(partial)
break
if ans:
break
"""
[3, 4, 5]
"""
3. 다이나믹 프로그래밍
이번엔 수열의 순서를 인덱스로 하여 수열을 리스트에 저장하면..
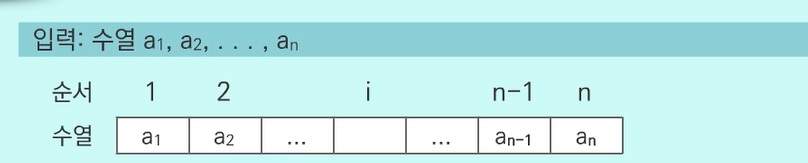
DP[i]가 부분수열 $a_{1}, a_{2}, ..., a_{i}$에 존재하는 가장 긴 증가 부분수열의 길이라고 하자.
그러면 i보다 길이가 작은 수열내에 존재하는 가장 긴 증가 부분수열의 길이는?
DP[1], DP[2], ..., DP[i-1]로 나타낼 수 있을 것이다.
만약 DP[i]가 수열의 마지막 원소인 $a_{i}$를 포함하지 않는다면...
생각할 필요도 없이 당연히 DP[i]는 DP[i-1]과 같다.
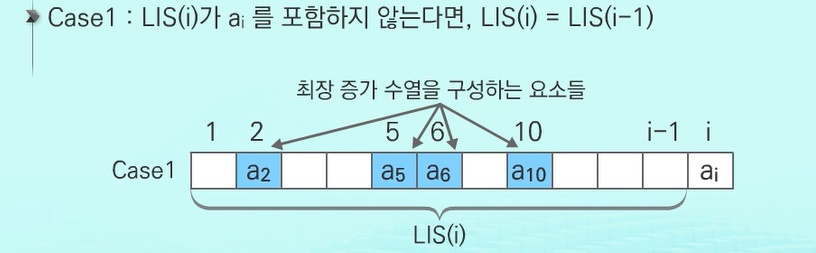
반대로 만약 DP[i]가 수열의 마지막 원소인 $a_{i}$를 포함한다면... 이제는 까다로워진다.
DP[i-1]에 $a_{i}$를 포함시켜서 1을 더하면 되나???

하지만 그것이 가능할려면 위 그림에서 볼 수 있듯이, DP[i-1]의 마지막 원소가 DP[i]의 마지막 원소보다 작아야한다

최장 증가 수열을 예로 들어 구해본다면 위의 표와 같이 정리되는데,
특징은 "반드시 $a_{i}$로 끝난다는 점"이다... (근데 당연한게 $a_{i}$로 끝나는 수열을 내가 찾은거니까 당연한거였어)
그래서 $a_{i}$로 끝나는 최장 증가 수열들 중에서도 가장 긴 수열이 전체 수열에서 최장 증가 수열이 된다
예를 들어, 만약 $a_{1}$, $a_{2}$, $a_{3}$, $a_{4}$로 끝나는 최장 증가 수열의 길이를 구했다고 가정할때,
$a_{5}$로 끝나는 최장 증가 수열은?

$a_{5}$보다 뒤에 있으면서, $a_{5}$보다 작은 값들은 $a_{1}$, $a_{2}$, $a_{4}$이다.
그러므로, $a_{1}$으로 끝나는 최장 증가 수열(길이 1)에 $a_{5}$를 포함시키면, 그 수열의 길이는 2이고
$a_{2}$로 끝나는 최장 증가 수열(길이 1)에 $a_{5}$를 포함시키면, 그 수열의 길이는 2이고
$a_{4}$로 끝나는 최장 증가 수열(길이 2)에 $a_{5}$를 포함시키면, 그 수열의 길이는 3이다
--------------------------------------------------------------------------------------------------------------------------------------
따라서 이러한 알고리즘을 정리해보면 다음과 같다.
i개의 부분수열 $a_{1}, a_{2}, ..., a_{i}$에서 마지막 원소 $a_{i}$를 포함하는 최장 증가 부분수열의 길이 DP[i]는...
$a_{i}$보다 작은 $a_{j}$를 처음부터 검색해서 모두 찾는다. (j < i)
그러면, $a_{j}$로 끝나는 최장 증가 부분수열에 $a_{i}$를 포함시키면, 그것이 $a_{i}$를 포함하는 최장 증가 부분수열이다.
따라서, $a_{j}$로 끝나는 최장 증가 부분수열의 길이들 중 최댓값에 1을 더하면 DP[i]가 된다.
DP[i] = max(DP[j]) + 1,
j < i and $a_{i}$ > $a_{j}$
그러므로 모든 i=1,2,3,..,n에 대하여 DP[i]를 구했다면, 전체 수열 $a_{1}, a_{2}, ..., a_{n}$에서 가장 긴 증가 부분수열의 길이는... DP의 최댓값이 된다.
4. 다이나믹 프로그래밍 구현 예시
#다이나믹 프로그래밍으로 최장증가 부분수열 찾기
s = [3,2,6,4,5,1]
n = len(s)
dp = [0]*(n+1)
for i in range(1,n): ##1번부터 n-1번까지
dp[i] = 1 ##최초 1로 시작
for j in range(1,i): ##인덱스 i이전의 j에 대하여
##a_i보다 작은 a_j를 찾는다
if s[j] < s[i]:
##그러면, dp[i]는 1+dp[j]중 최댓값
if dp[i] < 1+dp[j]:
dp[i] = 1+dp[j]
print(max(dp)) ##dp테이블에서 최댓값이 전체 수열에서 가장 긴 증가 부분수열의 길이
"""
3
"""
5. 이진탐색을 이용한 개선된 알고리즘
이제는 "$a_{i}$보다 작은 $a_{j}$를 처음부터 검색해서 모두 찾는다. (j < i)" 이 부분이 비효율적이다는 것이다.
수열의 원소를 읽어들이면서 "가장 긴 증가 부분수열의 마지막 원소가 가능하면 작을수록 더 긴 증가하는 부분수열을 생성할 수 있다"
DP[i] = k를 만족하는 증가하는 수열에 대하여, $a_{i}$가 가장 작은 경우 그 값을 어떤 배열 C에 저장해둔다.
수열 8 2 4 3 6 11 7 10 14 5을 생각해보자.
먼저 8을 읽어들이면, 길이 1인 증가하는 부분수열의 가장 끝값은 8이다.

다음 2를 읽어들이는데, 배열 C에서 2보다 작은 값중 가장 큰값 다음에 2를 붙인다
길이 1인 증가하는 부분수열은 8과 2가 있는데.. 8을 기억하는 것보다 2를 기억하고 있어야.. 더 긴 증가하는 부분수열을 만들기에 유리하다.
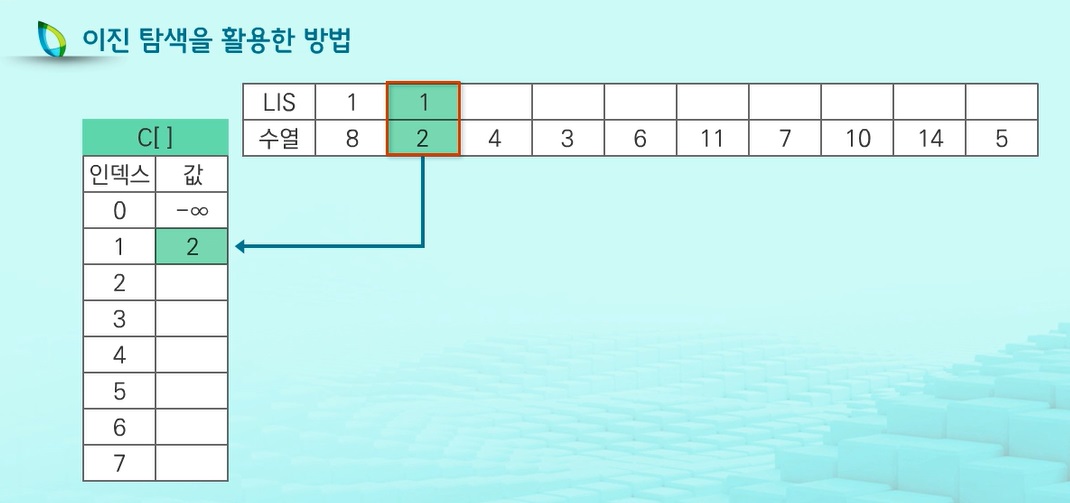
다음 4를 읽어들이면.. 4보다 작으면서 가장 큰값의 위치는 1번인데 현재 C[1]=2가 무슨말일까?
이는 길이 1인 증가하는 부분수열중 마지막 원소가 2인 부분수열이 있다는 말이다.
그러한 부분수열에 4를 붙이면, 길이가 2인 증가하는 부분수열이 된다.

다음에 3을 읽어보면.. 역시 3보다 작은 값들 중에 가장 큰 값의 위치를 찾는다. 그것은 1번이고..
길이가 1인 증가하는 부분수열중 마지막 원소가 2로 끝나는 수열이 있다는 뜻이다.
4보다 3을 붙여서 {2,3}을 기억하고 있으면 더 긴 증가 부분수열을 만들기에 유리하다.
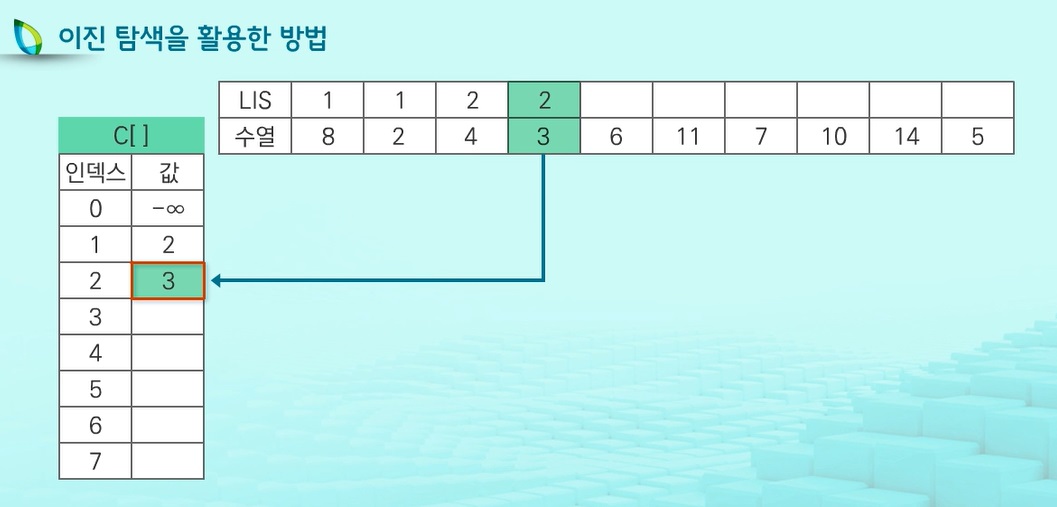
다음 6을 읽어서 C배열에서 6보다 작은 값들 중 가장 큰 값의 위치를 찾는다.
그것은 2번이고 이는 길이가 2인 증가하는 부분수열중 마지막 원소가 3으로 끝나는 수열이 있다는 뜻이다.
그리고 그 뒤에 6을 붙이면 길이가 3인 증가하는 부분수열이 된다.

마찬가지로 11을 읽고 C배열에서 11보다 작은 값 중에서 가장 큰 값인 6 뒤에 붙여주면.. 길이가 4인 증가하는 부분수열이 된다.
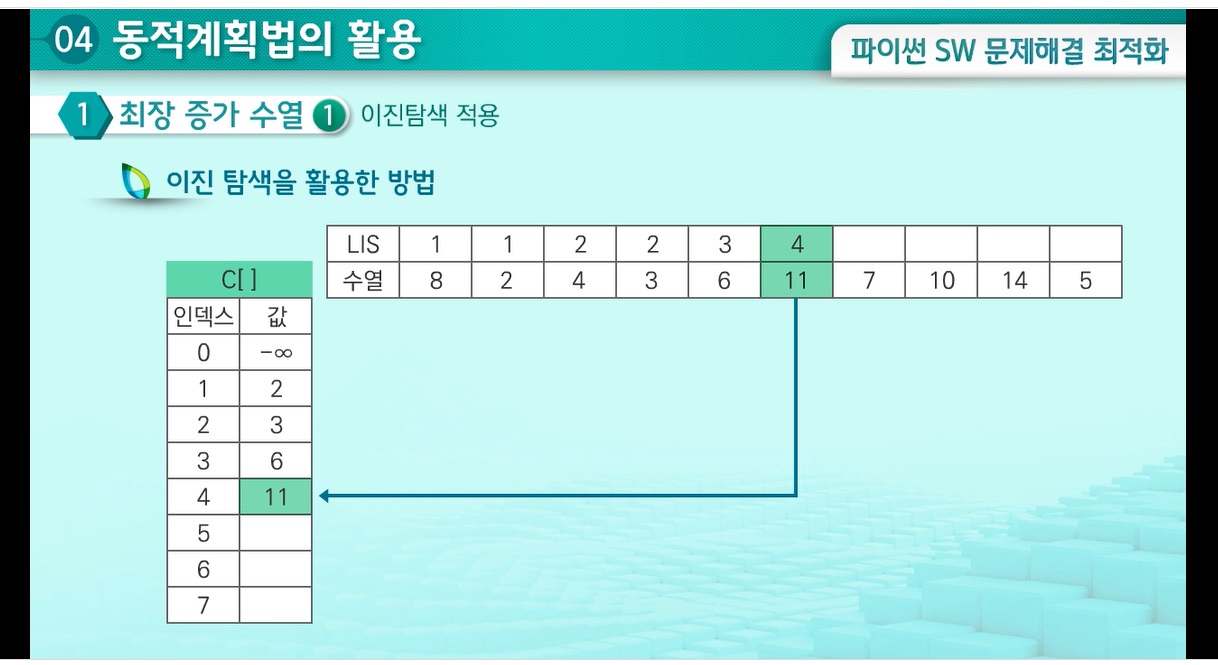
마찬가지로 7을 읽어서.. 7보다 작은 값중에 가장 큰 값인 6을 찾아 그 뒤에 붙여주면.. {2,3,6,11}보다는 {2,3,6,7}을 만들어놓으면 그것이 더 긴 증가하는 부분수열을 만들기에 유리하다.

10,14도 읽어들이면.. 마찬가지 원리로 각각 5번 6번에 저장되겠지

그러면.. 마지막 5를 읽어들이는데 역시 5보다 작은 값중에서 가장 큰 값인 3의 위치를 찾고..
그 뒤에 붙여준다면?? 5로 끝나는 부분 수열중에 가장 긴 것이 {2,3,5}라는 뜻이다
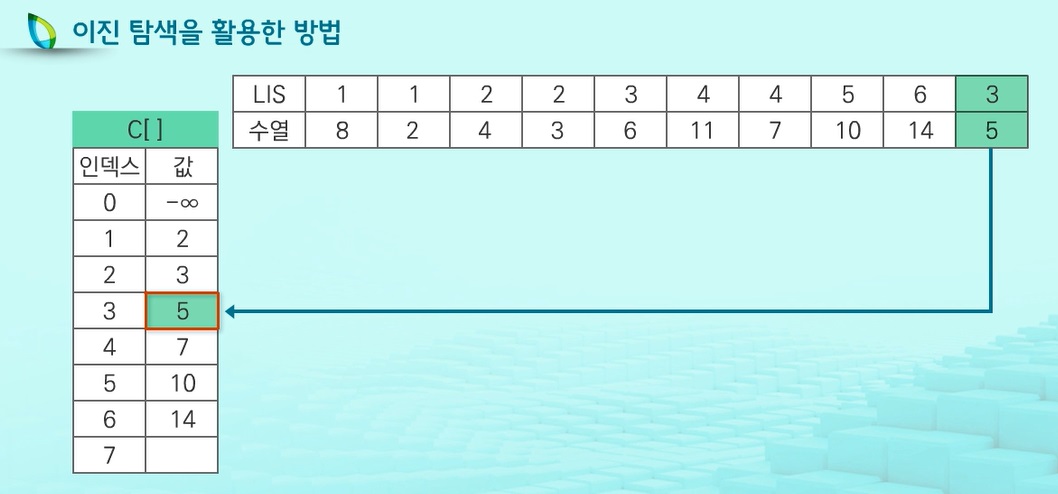
C배열의 길이 6이 전체 수열에 존재하는 가장 긴 증가하는 부분수열의 길이이다.
근데 왜 이진탐색이냐고??
lower bound 알고리즘은 수많은 값들 중에서 target값이 가장 먼저 나오는 위치를 찾는 알고리즘이였다.
그렇다면 내가 넣고자 하는 수 a[i] 보다 작은 값중에서 가장 큰 값의 위치 다음에 내가 넣고자 하는 수 a[i]를 넣을건데
"내가 넣고자 하는 수 a[i] 보다 작은 값중에서 가장 큰 값의 위치 다음"은 바꿔말하면,
"a[i]보다 크거나 같은 값들 중에서, 가장 작은 값의 위치"와 동일하고.. 이는 lower bound 알고리즘으로 찾을 수 있다.
6. 이진탐색을 이용한 증가하는 부분수열 찾기 구현 예시
파이썬의 라이브러리로 구할 수 있기는 한데, 일단 내가 구현했었던 lower bound함수를 이용해서 구현해보도록 한다면..
최초 c배열을 매우 큰 수들을 넣은 배열로 초기화한다
그러면 lower bound알고리즘이 end값이 c배열의 길이를 넘어갈리가 없다
그러니까 lower bound는 end가 무조건 0~n-1중에 하나가 된다는 소리
현재 가장 긴 증가하는 부분수열의 길이 LIS를 기억하고
찾아낸 위치와 LIS를 비교한다..
서로 같다면 C배열에서 가장 큰 수를 읽은 것으로, 가장 긴 증가하는 부분수열의 길이를 1 증가함
그렇지 않다면 그냥 그 위치에 숫자를 넣어주면 된다
#이진탐색으로 최장증가 부분수열 찾기
##배열에서 읽어들인 숫자보다 크거나 같은 최초의 위치를 찾는다
def lower_bound(array,target,start,end):
while start < end:
mid = (start+end)//2
if array[mid] >= target:
end = mid
else:
start = mid + 1
return end
s = [8,2,4,3,6,11,7,10,14,5]
n = len(s)
c = [1000000000000000000000000000000]*n #매우 큰 값으로 c배열을 초기화
LIS = 0 #현재 가장 긴 증가하는 부분수열의 길이
for num in s: ##s에서 숫자를 처음부터 읽어들여..
##num보다 크거나 같은 값들 중에서 가장 작은 위치를 찾는다.
loc = lower_bound(c,num,0,n)
#찾은 위치가 현재 가장 긴 증가하는 부분수열과 같다면..
if loc == LIS:
c[LIS] = num # 그 위치에 숫자를 넣고
LIS += 1 #가장 긴 증가하는 부분수열의 길이를 1 증가
else:
c[loc] = num
print(LIS)
11053 가장 긴 증가하는 부분 수열 :: 끄적끄적 (tistory.com)
11053 가장 긴 증가하는 부분 수열
유형 : dp LIS(Longest Increasing Subsequence)로 알려진 유명한 문제이다. 주어진 배열에서 몇 개의 요소들을 제거하여 만들 수 있는 가장 긴 증가하는 수열을 찾는 문제로, 배열이 [1,3,5,2,1,6] 으로 주어
hellya.tistory.com
LIS (Longest Increasing Subsequence) - 최장 증가 부분 수열 (rebro.kr)
LIS (Longest Increasing Subsequence) - 최장 증가 부분 수열
주어진 수열에서 <최장 증가 부분 수열 (Longest Increasing Subsequence)> 을 구하는 문제 유형을 알아보자. 사실 이 유형은 DP(Dynamic Programming) 문제로 자주 나오는 유형이며, O(N^2)의 시간복잡도를 갖는..
rebro.kr
'알고리즘 > 다이나믹 프로그래밍' 카테고리의 다른 글
| 가장 긴 증가 부분수열 실제 수열을 구하는 역추적 방법 (0) | 2022.10.26 |
|---|---|
| 다이나믹 프로그래밍의 기본이 되는 동전 거스름돈 문제 해법 배우기 (0) | 2022.10.22 |
| 배낭(Knapsack) 문제, 다이나믹 프로그래밍 해법 배우기 (0) | 2022.10.19 |
| 다이나믹 프로그래밍 연습하기 -수영장- (0) | 2022.10.08 |
| 다이나믹 프로그래밍 정복 -피보나치 변형 몇가지- (0) | 2022.09.20 |

