1. 배낭 문제 개요
n개의 물건이 존재하고, 각 물건 i의 무게는 $w_{i}$, 가치가 $v_{i}$로 주어진다.
배낭의 용량이 W라고 할때, 이러한 배낭에 담을 수 있는 물건의 최대 가치는?

단, 배낭에 담은 물건의 무게 합은 W를 초과할 수 없고 각각의 물건은 1개씩만 존재한다
그리고 물건을 쪼개서 담을 수 없다고 가정한다. 이러한 문제는 0-1 knapsack 문제라 부르고
물건을 쪼개서 담을 수 있는 경우도 물론 있는데 fractional knapsack 문제라고 부른다.
2. 해법 - 완전탐색
조금 생각해보면, 존재하는 물건들의 집합 S에서, 일부를 골라 가방에 담는 문제이므로,
집합 S에서 모든 부분집합을 구하고, 가치들의 합을 조사한다
이때, 가방의 용량을 넘지 않으면 가치의 합을 구하고, 최댓값을 갱신한다
가방의 용량을 넘으면 그러한 부분집합은 버린다
3. 완전탐색 예시
4개의 물건이 존재하고 각각 무게와 가치가
(5,10), (4,40), (6,30), (3,50)이라고 하자. 배낭 무게가 10일때, 최대가치로 담을 수 있는 경우는?
#완전 탐색을 이용한 0-1 knapsack 해법
n = 4 ##물건의 개수
s = [(5,10),(4,40),(6,30),(3,50)] ##가능한 물건들
w = 10 ##가방 무게
max_value = 0 ##최대가치
max_list = [] ##최대가치일때 경우의 수
##s의 모든 부분집합을 조사
for i in range(1<<n):
partial_w = 0
partial = []
partial_v = 0
for j in range(n):
if i & (1<<j):
partial_w += s[j][0] #부분집합으로 선택된 물건의 무게 누적합
partial.append(s[j])
partial_v += s[j][1] #부분집합으로 선택된 물건의 가치 누적합
if w >= partial_w: ##담은 물건의 무게가 가방 용량을 넘지 않으면..
if max_value < partial_v: ##최대 가치를 갱신하는 경우..
max_value = partial_v
max_list = partial[:]
print(max_value)
print(max_list)
"""
90
[(4, 40), (3, 50)]
"""
4. 부분 문제 정의
물건들의 집합 {1,2,3,4,5,...,n}에 대하여.. n번째 물건을 배낭에 담느냐, 담지 않느냐로 나눌 수 있다

n번째 물건을 담은 경우, 담을 수 있는 물건들은 {1,2,...,n-1}이고, 남은 용량은 $W-w_{n}$
n번째 물건을 담지 않은 경우, 담을 수 있는 물건들은 {1,2,...,n-1}이고, 남은 용량은 W
왜 {1,2,...,n-1}이냐고? n번은 안담기로 했으니까
5. 다이나믹 프로그래밍
그러면 바텀업 방식으로 아래서부터 위로 올라올때, n번째 물건을 담기 전까지 가치를 구해올 수 있을 것이다.
그런데 2가지 경우가 생긴다.
1) n번째 물건을 담기 전의 가치 + n번 물건의 가치
2) n번째 물건을 담지 않을때 가치
따라서 배낭문제의 최적해는,
max( < n번째 물건을 담기 전의 가치 + n번 물건의 가치>, <n번째 물건을 담지 않을때 가치> )

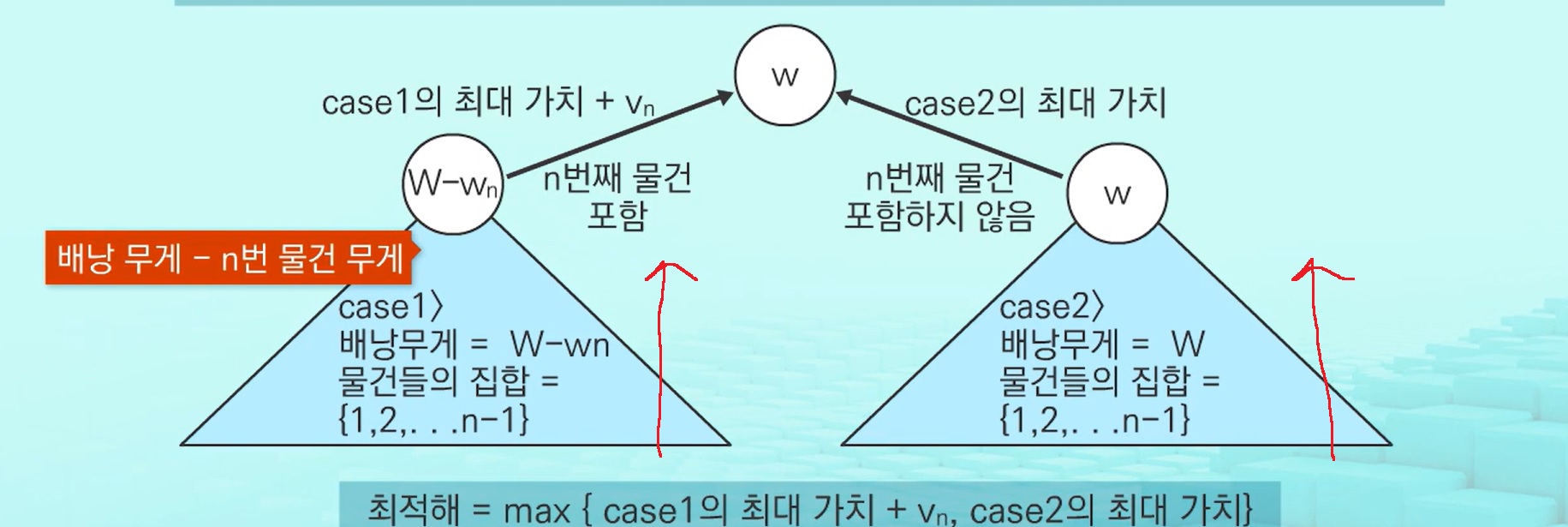
dp 테이블을 K[n][W]라고 정의하자.
K[n][W]는 1~n번까지의 물건 [1,2,3,...,n]중에서 배낭 최대 무게 W를 넘지 않는 선에서 담을때 최대 가치
그러면 K[n-1][W]는 [1,2,3,...,n-1]중에서 배낭 최대 무게 W를 넘지 않는 선에서 담을 때 최대 가치
K[n-1][W-wn]은 [1,2,3,...,n-1]중에서 배낭 최대 무게 W-wn을 넘지 않는 선에서 담을 때 최대 가치
그러므로, K[n][W] = max(K[n-1][W-wn]+vn , K[n-1][W])라는 점화식을 세울 수 있다.
------------------------------------------------------------------------------------------------------------------------------
그러면.. 여기서 내가 원하는 K[n][W] 는 어떻게 구했지??
다이나믹 프로그래밍 할때, n=0, W=0부터 n,W까지 자연스럽게 채워나갔지..
초기값 n=0, W=0이면? K[0][0] = 0
그러면 n=1,2,3,...일때는?? 큰 문제가 되지 않는다.. 물건의 후보만 달라질뿐
n=1이면 {1}에서만 배낭에 담을 수 있고
n=2이면 {1,2}에서만 배낭에 담을 수 있다
n=3이면 {1,2,3}에서만 배낭에 담을 수 있다
..
하지만 W=0,1,2,...에서는? 배낭에 담을 수 있는 후보 집합 {1,2,...,n}에서 다음에 담을 물건은 n번인데..
이 n번의 무게 $w_{n}$이 남아있는 배낭의 무게 W보다 크다면, n번은 담을 수 없으므로...
K[n][W] = K[n-1][W]
하지만 $w_{n}$이 남아있는 배낭의 무게 W보다 작거나 같다면.. n번은 이제 담을 수 있으므로...
n번을 담은 경우와 n번을 담지 않은 경우로 나누어서 문제를 푼다
K[n][W] = max(K[n-1][W-wn]+vn , K[n-1][W])

6. 재귀함수를 이용한 메모이제이션 구현 예시
위 알고리즘을 그대로 재귀함수를 이용해서 구현해본다면..
def knapsack(i,W,dp,weight,value):
##-1이 아니라면, 물건이 담긴 경우다
if dp[i][W] != -1:
return dp[i][W]
##물건을 담을 수 없거나 물건이 없는 경우
if i == 0 or W == 0:
dp[i][W] = 0
return dp[i][W]
else: ##물건이 존재하는 경우
case1 = 0
if W >= weight[i]: ##담을 물건 i가 남은 무게 W보다 작은경우
case1 = knapsack(i-1, W-weight[i],dp,weight,value) + value[i]
##case1이 구해지지 않으면, case1=0과 case2사이 최댓값 갱신
##case1이 구해지면, case1,case2사이 최댓값 갱신
case2 = knapsack(i-1,W,dp,weight,value)
dp[i][W] = max(case1,case2)
return dp[i][W]
n = 4 ##물건의 개수
weight = [0,5,4,6,3]
value = [0,10,40,30,50]
w = 10 ##가방 무게
dp = [[-1]*(w+1) for _ in range(n+1)]
print(knapsack(n,w,dp,weight,value))
"""
90
"""
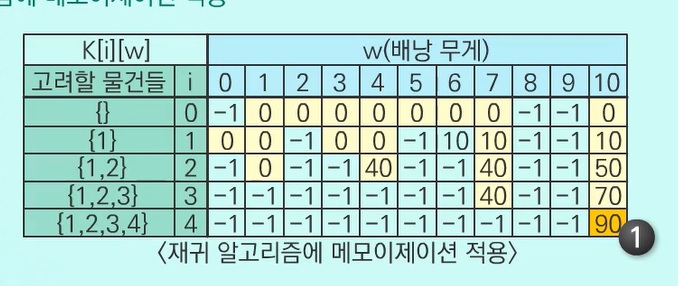
-1로 초기화된 K table을 점화식에 따라 채워나가서, 마지막 K[4][10]을 구하는 과정이다.
7. 반복문을 이용한 다이나믹 프로그래밍 구현 예시
재귀함수보다는 반복문을 사용하는게 낫겠지.. ? 하던대로 반복문으로 위와 같은 표를 채워나간다고 생각해보자
점화식은 이미 설명했다
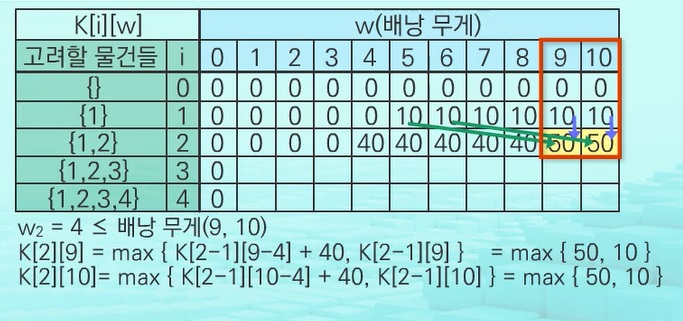
K[n][W]를 구하기 위해서는...? K[n-1][W]와 K[n-1][W-w_n]가 필요하다
무슨 말이냐면.. n번째 행의 값을 구하기 위해서는 미리 n-1행의 값을 모두 구해와야한다는 뜻이다
그런데 -1행은 없잖아.. 그러니까 0행을 미리 구해야해.. 0행은 규칙에 따라 구할 수 있겠지..?
K[0][W]는 뭐겠어..? 아무런 물건도 담는 경우가 아니니까 모든 W에 대하여, K[0][W]=0이겠지
마찬가지로... 모든 i에 대하여 W가 0인 경우는... 어떤 물건이 있더라도 담을수가 없으니까
K[i][0] = 0
다음 1행 1열부터 이제 점화식을 이용해서 채워나가는 것이다
담을 물건 i의 무게가 남아있는 무게 w 이상이라면, 담을수가 없고 적다면 담을수가 있었잖아
n = 4 ##물건의 개수
weight = [0,5,4,6,3]
value = [0,10,40,30,50]
w = 10 ##가방 무게
dp = [[-1]*(w+1) for _ in range(n+1)]
##0행과 0열을 채운다
##물건이 존재하지 않으면.. 담을 수 없으므로 가치는 0
for W in range(w+1):
dp[0][W] = 0
##남은 용량이 없으면.. 담을수 없으므로 가치는 0
for i in range(n+1):
dp[i][0] = 0
#1행 1열부터 채워넣는다
for i in range(1,n+1):
for W in range(1,w+1):
if W >= weight[i]: ##담을 물건 i의 무게가.. 남아있는 물건의 무게 이하라면..
##해당 물건은 담을 수 있으므로..
dp[i][W] = max(dp[i-1][W-weight[i]]+value[i], dp[i-1][W])
else: ##무게가 i번이 남은 용량보다 더 커서 담을 수 없다면..
dp[i][W] = dp[i-1][W]
print(dp[n][w])
"""
90
"""
아니 이거 파이프 옮기기 그 문제랑 사실상 똑같은 문제였네?
'알고리즘 > 다이나믹 프로그래밍' 카테고리의 다른 글
| 다이나믹 프로그래밍의 기본이 되는 동전 거스름돈 문제 해법 배우기 (0) | 2022.10.22 |
|---|---|
| 다이나믹 프로그래밍 - 최장 증가 수열(LIS)을 찾는 알고리즘 배우기 (0) | 2022.10.20 |
| 다이나믹 프로그래밍 연습하기 -수영장- (0) | 2022.10.08 |
| 다이나믹 프로그래밍 정복 -피보나치 변형 몇가지- (0) | 2022.09.20 |
| 다이나믹 프로그래밍 정복기4 - 규칙을 찾으면 되는 쉬운문제들1- (0) | 2022.09.09 |

