1. 문제
17070번: 파이프 옮기기 1 (acmicpc.net)
17070번: 파이프 옮기기 1
유현이가 새 집으로 이사했다. 새 집의 크기는 N×N의 격자판으로 나타낼 수 있고, 1×1크기의 정사각형 칸으로 나누어져 있다. 각각의 칸은 (r, c)로 나타낼 수 있다. 여기서 r은 행의 번호, c는 열의
www.acmicpc.net
17069번: 파이프 옮기기 2 (acmicpc.net)
17069번: 파이프 옮기기 2
유현이가 새 집으로 이사했다. 새 집의 크기는 N×N의 격자판으로 나타낼 수 있고, 1×1크기의 정사각형 칸으로 나누어져 있다. 각각의 칸은 (r, c)로 나타낼 수 있다. 여기서 r은 행의 번호, c는 열의
www.acmicpc.net
n*n에서 조건에 맞게 (0,0)에서 시작해서 (n-1,n-1)까지 파이프를 옮겨 붙이는 방법의 수를 구하는 문제
2. 풀이
어떤 지점 (x,y)에 파이프가 올 수 있는 방법의 수를 dp배열에 저장해가면서, (0,0)부터 (n-1,n-1)까지 상향식으로 채워나간다.
파이프가 어떤 지점 (x,y)로 들어올 수 있는 방법은?
1)왼쪽에서 오른쪽으로 들어오기
2)위에서 아래로 들어오기
3)대각선으로 들어오기

from sys import stdin
n = int(stdin.readline())
maps = [list(map(int,stdin.readline().split())) for _ in range(n)]
dp = [[[0,0,0] for _ in range(n)] for _ in range(n)]
dp[0][1][0] = 1
그래서 dp배열을 3차원으로 생성한다.
i = 0이면 왼쪽에서 오른쪽으로
i = 1이면 위에서 아래로
i = 2이면 대각선으로
dp[y][x][i]는 (x,y)로 i방향으로 들어오는 경우의 수를 의미한다고 하자.
dp = [[[0,0,0] for _ in range(n)] for _ in range(n)] 으로 생성하면 될거야
[ [0,0,0] [0,0,0] [0,0,0] [0,0,0] [0,0,0] ]
[ [0,0,0] [0,0,0] [0,0,0] [0,0,0] [0,0,0] ]
[ [0,0,0] [0,0,0] [0,0,0] [0,0,0] [0,0,0] ]
[ [0,0,0] [0,0,0] [0,0,0] [0,0,0] [0,0,0] ]
[ [0,0,0] [0,0,0] [0,0,0] [0,0,0] [0,0,0] ] << 5*5 예시..
그러면 최초 상태는? 가로로(왼쪽에서 오른쪽으로) (1,0)에 놓이는 1가지
dp[0][1][0] = 1
문제 조건상, 가로로 놓인 경우는 가로로 붙이거나, 대각선으로 붙이거나만 가능하므로
우리는 탐색가능한 공간은?
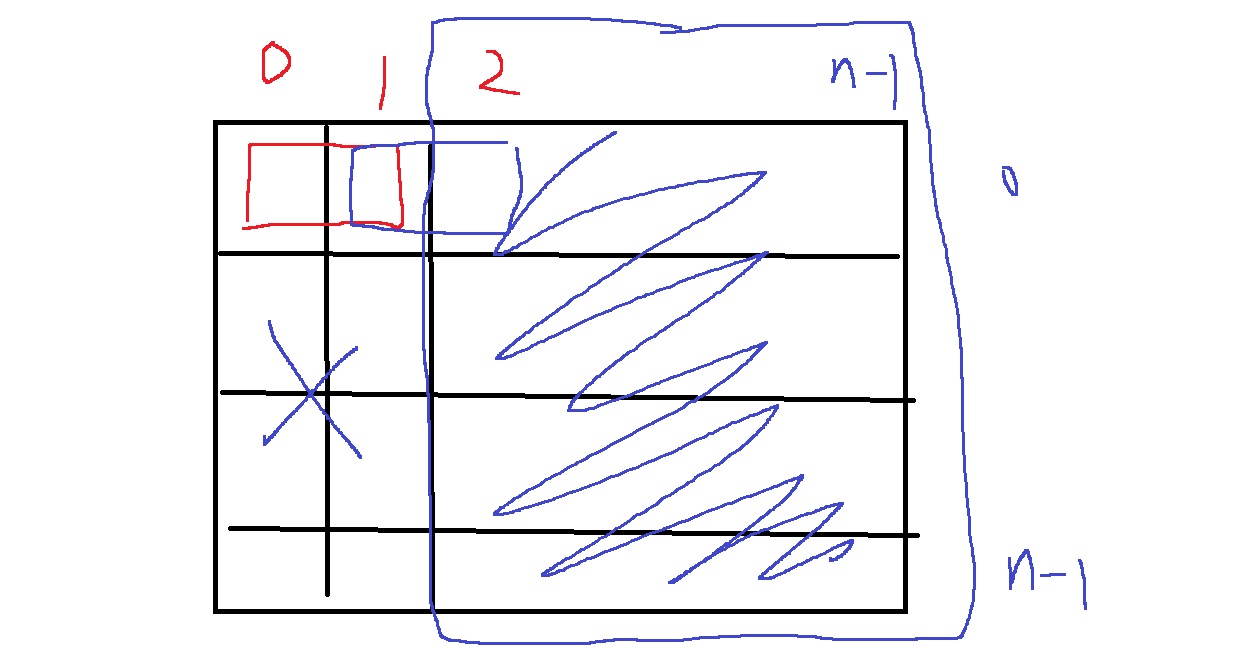
x는 2~n-1까지, y는 0~n-1까지 가능하다
그러면 이제 (x,y)지점으로 들어오는 방법의 수를 점화식 형태로 만들어서 구해보는 것이다.
그러면 (x,y)지점에 왼쪽에서 오른쪽으로 들어오는 방법은?

먼저 위와 같이 (x-1,y)지점에 대각선으로 들어오는 경우, 다음 (x,y)에 가로로 붙이면 된다
이거는 dp[y][x-1][2] <(x-1,y)에 대각선으로 들어오는 경우의 수>로 나타낼 수 있을 것
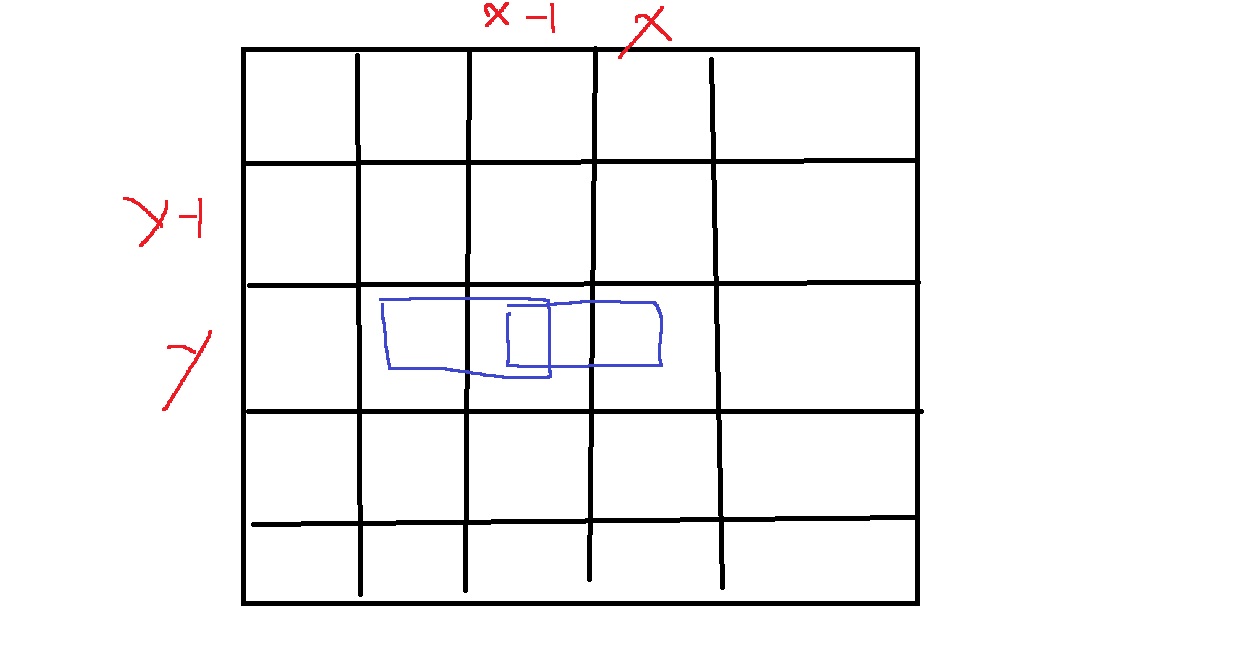
다음은 위와 같이 (x-1,y)에 가로로 들어온 경우, 다음 (x,y)에 가로로 붙이면 된다
이거는 dp[y][x-1][0]<(x-1,y)에 가로로 들어오는 경우의 수>로 나타낼 수 있다.
따라서, dp[y][x][0] = dp[y][x-1][0] + dp[y][x-1][2]
비슷하게, (x,y)지점을 위에서 아래로 들어오는 경우는 어떻게 구할 수 있을까
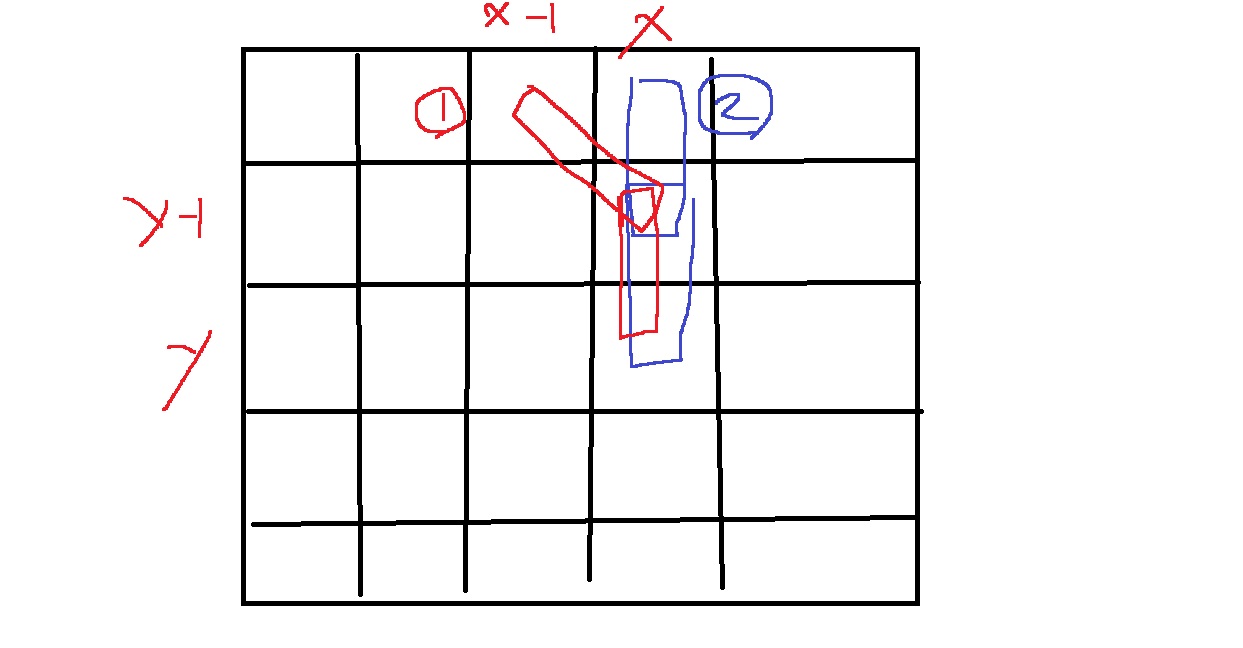
위와 같이 (x,y-1)에 대각선으로 들어오는 경우(1)와 위에서 아래로 들어오는 경우(2)를 합하면 된다
(x,y-1)에 대각선으로 들어오는 경우는.. dp[y-1][x][2]이고
(x,y-1)에 위에서 아래로 들어오는 경우는.. dp[y-1][x][1]이다.
그러므로, (x,y)에 위에서 아래로 들어오는 경우란.. dp[y][x][1] = dp[y-1][x][1] + dp[y-1][x][2]
근데 파이프가 (x,y)로 들어오는 조건이 있다.
그거는 map상에 (x,y)지점에 벽이 없어야한다. 즉 maps[y][x]가 1이 아니어야 한다.
for y in range(n):
for x in range(2,n):
if maps[y][x] == 1:
continue
dp[y][x][0] = dp[y][x-1][0] + dp[y][x-1][2]
dp[y][x][1] = dp[y-1][x][1] + dp[y-1][x][2]
다음으로 (x,y)에 대각선으로 들어오는 경우를 생각해보자.

위와 같이 (x-1,y-1)에 대각선으로 들어오거나, 가로로 들어오거나, 위에서 아래로 들어오거나
모든 경우에 (x,y)에 대각선으로 들어갈 수가 있다.
각각 (x-1,y-1)에 대각선으로 들어가는 경우는 dp[y-1][x-1][2]
가로로 들어오는 경우는.. dp[y-1][x-1][0]
세로로 들어오는 경우는.. dp[y-1][x-1][1]
그러므로, (x,y)에 대각선으로 들어오는 경우의 수는...
dp[y][x][2] = dp[y-1][x-1][0] + dp[y-1][x-1][1] + dp[y-1][x-1][2]
그런데 이렇게 들어오는게 가능할려면?

문제 조건에서 대각선으로 들어올려면 위에서 보라색 부분이 절대로 벽이 아니어야 한다.
즉, maps[y][x-1]이나 maps[y-1][x]가 하나라도 1이면, (x,y)지점에 대각선으로 들어올 수는 없다
(x,y)지점도 체크해야하냐고? 아니다.. 이미 가로, 세로로 (x,y)에 들어가는 경우에 maps[y][x]가 1인지 아닌지 검사했다
if maps[y-1][x] == 1 or maps[y][x-1] == 1:
continue
dp[y][x][2] = dp[y-1][x-1][0] + dp[y-1][x-1][1] + dp[y-1][x-1][2]
따라서 모든 경우를 조합하면... dp[n-1][n-1]에 가로, 세로, 대각선으로 (n-1,n-1)에 들어가는 방법의 수가 있을 것이다
from sys import stdin
n = int(stdin.readline())
maps = [list(map(int,stdin.readline().split())) for _ in range(n)]
#i=0 가로
#i=1 세로
#i=2 대각선으로 (x,y)지점에 가는 방법의 수
dp = [[[0,0,0] for _ in range(n)] for _ in range(n)]
#초기 상태, (1,0)에 가로로 1가지 가능
dp[0][1][0] = 1
#문제 조건에 의해, x는 2~n-1, y는 0~n-1인 영역만 파이프가 존재할 수 있다
for y in range(n):
for x in range(2,n):
##가로로 들어오는 경우와 세로로 들어오는 경우를 센다
##애초에 (x,y)가 벽이면 (x,y)에는 파이프가 들어갈 수가 없다
if maps[y][x] == 1:
continue
#가로(0)으로 들어가는 방법의 수
dp[y][x][0] = dp[y][x-1][0] + dp[y][x-1][2]
#세로(1)로 들어가는 방법의 수
dp[y][x][1] = dp[y-1][x][1] + dp[y-1][x][2]
#대각선으로 들어오는 경우를 센다
#(x,y-1)과 (x-1,y)가 벽이 아니어야 대각선으로 (x,y)에 들어갈 수 있다
if maps[y-1][x] == 1 or maps[y][x-1] == 1:
continue
#(x,y)에 대각선으로 들어가는 방법의 수
dp[y][x][2] = dp[y-1][x-1][0] + dp[y-1][x-1][1] + dp[y-1][x-1][2]
#for문을 전부 돌아 dp배열을 채우면.. (n-1,n-1)에 경우의 수가 존재함
print(dp[n-1][n-1][0] + dp[n-1][n-1][1] + dp[n-1][n-1][2])'알고리즘 > 다이나믹 프로그래밍' 카테고리의 다른 글
| 조금 더 어려운 다이나믹 프로그래밍 연습하기 -퇴사1,2- (0) | 2022.11.07 |
|---|---|
| dictionary와 재귀를 이용한 다이나믹 프로그래밍 기본 테크닉 배우기1 (0) | 2022.11.07 |
| 가장 긴 증가 부분수열 실제 수열을 구하는 역추적 방법 (0) | 2022.10.26 |
| 다이나믹 프로그래밍의 기본이 되는 동전 거스름돈 문제 해법 배우기 (0) | 2022.10.22 |
| 다이나믹 프로그래밍 - 최장 증가 수열(LIS)을 찾는 알고리즘 배우기 (0) | 2022.10.20 |

