1. 52개의 카드를 이용해서 만들 수 있는 5개 카드 조합 중 같은 무늬의 카드가 정확히 3개인 경우의 수
52개의 카드에는 4가지 무늬가 존재하는데, 그러한 4가지 무늬중 같은 무늬로 만들 3개의 카드를 구성하기 위한 무늬를 고르는 경우의 수는.. $\binom{4}{1}$
선택한 무늬에서 3개의 카드를 선택하는 경우의 수는.. 13가지 중에서 3장을 뽑아야하므로 $\binom{13}{3}$
나머지 2장은 다른 무늬의 카드에서 골라야한다.
남은 3가지 무늬 중에서 2가지를 뽑는 방법의 수는$\binom{3}{2}$이고,
각각의 무늬에서 1장씩 뽑아야 정확히 3장만 같은 무늬를 가진다.
$\binom{13}{1}\binom{13}{1}$
따라서, $\binom{4}{1}\binom{13}{3}\binom{3}{2}\binom{13}{1}\binom{13}{1}$ = 580008가지
2. 비밀번호가 0부터 9까지의 숫자만 가지고 만든다. 4개이상 6개이하의 숫자를 쓴다고 할 때, 비밀번호의 가지수는?
중복숫자를 안쓴다고 할 때
4개의 숫자를 쓴다고 할 때, 0부터 9까지 중 첫번째 자리를 고르는 경우의 수는 $\binom{9}{1}$
2번째 자리를 고르는 경우의 수는 $\binom{8}{1}$
3번째 자리를 고르는 경우의 수는 $\binom{7}{1}$
4번째 자리를 고르는 경우의 수는 $\binom{6}{1}$
그러므로 4자리의 비밀번호를 구성하는 수는 9*8*7*6 = 3024
비슷하게 5자리의 비밀번호를 구성하는 수는 9*8*7*6*5 = 15120
비슷하게 6자리의 비밀번호를 구성하는 수는 9*8*7*6*5*4 = 60480
따라서 4~6자리의 비밀번호를 구성하는 수는 3024 + 15120 + 60480 = 78624
3. 스무고개가 이상적으로 진행된다고 할 때, 맞출 수 있는 답의 종류는?
스무고개로 20번 질문을 했을 때, 문제를 내는 사람이 문제를 맞추는 사람의 질문에 대하여 예/아니오로 대답을 한다.
그러면 이상적으로 진행될 때, 총 20번 질문을 수행하는 것이고, 이러한 질문에 대답할 수 있는 모든 경우의 수는 2*2*2*2*….*2 = $2^{20}$가지
그러므로 $2^{20}$가지의 정보를 얻은 경우에 대하여 최종 대답할 수 있는 모든 경우의 수는 $2^{20}$가지가 된다.
4. n이 충분히 큰 값일 때, 다음 중 어느 값이 더 큰지 각 쌍에 대해 비교하고 그 이유를 작성해라.
4-1) $2^{\frac{n}{2}}$와 $\sqrt{3^{n}}$
지수법칙에 의하여
$\sqrt{3^{n}} = 3^{\frac{n}{2}}$
지수함수 $y = 2^{x}$와 $y=3^{x}$를 그려보면
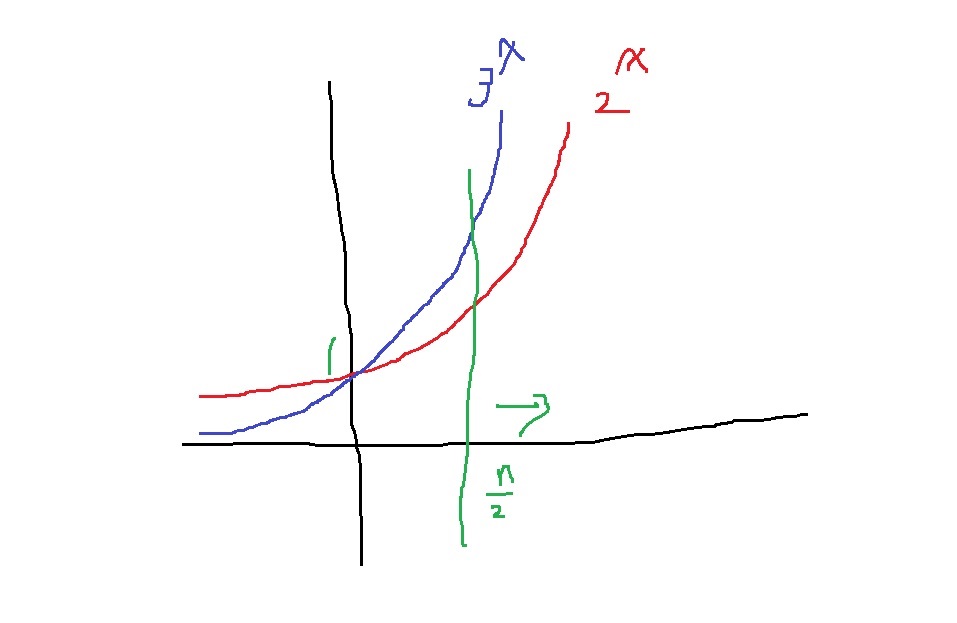
그러므로 x > 0에서 $y=3^{x}$가 항상 크다.
n이 충분히 크면 $\sqrt{3^{n}}$이 더 크다.
4-2) $log 2^{2n}$와 $n\sqrt{n}$
$log 2^{2n} = 2n$이다.
여기서 $\frac{n\sqrt{n}}{2n} = \frac{\sqrt{n}}{2}$인데, n이 충분히 크면
$\frac{\sqrt{n}}{2} >= 1$이므로, $n\sqrt{n}$이 더 크다.
5. f(x) = 3log(x+3) + 1의 역함수
식을 정리하면
f(x)-1 = 3log(x+3)
(f(x)-1)/3 = log(x+3)
$2^{(f(x)-1)/3} = x+3$
$x = 2^{(f(x)-1)/3} – 3$
따라서 f(x) = 3log(x+3) + 1의 역함수는 $y = 2^{(x-1)/3} – 3$
6. n개의 원소를 가진 집합의 가능한 부분집합의 개수는 $2^{n}$개?
(x1,x2,x3,…,x n)에서 부분집합은 원소를 0개 가지는 경우, 원소를 1개 가지는 경우, 원소를 2개 가지는 경우, …, 원소를 n개 가지는 경우가 존재한다.
그러면 그러한 부분집합의 개수는
$$\binom{n}{0} + \binom{n}{1} + \binom{n}{2} + ... + \binom{n}{n} = \sum_{k=0}^{n} \binom{n}{k}$$
그런데, 이항정리 $(x+y)^{n} = \sum_{k=0}^{n} \binom{n}{k} x^{n-k} y^{k}$에서, x=1, y=1이면
$2^{n} = \sum_{k=0}^{n} \binom{n}{k}$$
그러므로 n개의 원소를 가지는 집합의 부분집합의 개수는 $2^{n}$개
8. $(A\cup B) \cap (A\cap B)^{c}$이 사실임을 증명
드모르간의 법칙에 의해
$$(A \cup B) \cap (A \cap B)^{c} = (A \cup B) \cap (A^{c} \cup B^{c})$$
분배법칙에 의해
$$(A \cap A^{c} ) \cup ( B \cap A^{c}) \cup ( B \cap B^{c}) \cup (A \cap B^{c})$$
그런데
$(A \cap B^{c}) = A-B$이고 $(B \cap A^{c}) =B-A$이다.
그리고 $(A \cap A^{c}) = (B \cap B^{c}) = \phi$이다.
따라서,
$$(A \cap A^{c} ) \cup ( B \cap A^{c}) \cup ( B \cap B^{c}) \cup (A \cap B^{c}) = (A-B) \cup (B-A)$$
'프로그래밍 > 프로그래밍 개론' 카테고리의 다른 글
| Big O notation의 정의는 알고 쓰자 (0) | 2022.09.16 |
|---|---|
| 증명하기 연습문제2 (0) | 2022.09.15 |
| 귀류법과 수학적 귀납법 정확히 알기 (0) | 2022.07.13 |
| 논리학 연습문제1 (0) | 2022.07.12 |
| 반드시 알아야하는 기초 논리학 - p가 거짓이면 'p이면 q이다'는 왜 참인가? (0) | 2022.07.11 |

