1. 공허한 참
'p이면 q이다'라는 명제가 있을 때 일반적으로 p가 참이라고 생각하고 q의 참, 거짓을 통해 'p이면 q이다'가 참인지 거짓인지 파악한다
그러니까 p가 참이면 q가 참일때 'p이면 q이다'는 참이고 q가 거짓이면 'p이면 q이다'는 거짓이다
그렇다면 p가 거짓이면 어떤가? 'p이면 q이다'는 어떻게 파악하는가?
결론부터 말하면 p가 거짓이면 q의 참,거짓과 무관하게 'p이면 q이다'는 반드시 참이다. 이것을 공허한 참이라고 부른다
2. 사람들이 이야기하는 직관적인 이유
2-1)
내가 너에게 '이번 시험에 100점을 맞으면 치킨을 사주겠다'라고 약속을 함
100점을 받았는데, 치킨을 사줬다. >> 나는 약속을 지킴
100점을 받았는데, 치킨을 사주지 않았다 >> 나는 약속을 어김
100점을 못받았을때, 치킨을 안사줌 >> 나는 약속을 지킨거
100점을 못받았는데도, 치킨을 사줌 >> 치킨을 사주겠다는 약속을 분명히 지키긴함. 왜냐하면 '100점을 못받았을때는 안사주겠다라고 말하진 않았다'
그래서 가정 '100점을 맞으면'이 거짓이더라도 전체 명제 '100점을 맞으면 치킨을 사주겠다'는 반드시 참이다
2-2)
p이면 q이다가 거짓임을 보일 때 반례를 들어서 설명한다
반례라는 것은 p가 참이지만 q를 거짓으로 하는 것
하지만 p가 거짓이면 이러한 반례를 찾을 수가 없다
그러므로 p이면 q이다가 거짓임을 말할 수 있는 증거가 없다. 그래서 p이면 q이다는 참이라고 봐야한다
3. 수학적인 설명
3-1) 조건과 진리집합
조건은 미지수의 값에 따라 참,거짓이 결정되는 문장을 말한다
'x는 3보다 작다'라는 문장은 미지수 x에 따라 참,거짓이 달라진다. 이를 조건이라고 부른다
전체집합에서 조건이 참이되게하는 부분집합을 진리집합이라고 부른다
전체집합이 U = {x|x는 자연수}라고 하자. 그렇다면 p: 'x는 3보다 작다'의 진리집합은 P = {1,2}가 된다
3-2) 중요한 사실
1)항상 거짓인 조건의 진리집합은 항상 공집합이다?
항상 거짓인 조건이 있고 이것의 진리집합이 공집합이 아니다라고 가정해보면 공집합이 아닌 진리집합의 원소는 이 조건을 참으로 만들기 때문에 모순이 된다.
따라서 항상 거짓인 조건의 진리집합은 항상 공집합이다.
실제로 q: 'x는 2보다 큰 음의 정수이다'이고 U = {x|x는 자연수}라고 한다면 이를 만족하는 진리집합은 공집합이고 q는 항상 거짓이다
2)공집합은 모든 집합의 부분집합이다.
공집합이 있고, 공집합을 부분집합으로 가지지 않는 집합 A가 존재한다라고 가정하자.
이 가정은 바꿔말하면 'x가 공집합에 포함된다면 x가 A에 포함된다'를 만족하지 않는 어떤 원소 x가 존재한다.라는 뜻이다.
그렇지만 'x가 공집합에 포함된다'는 공집합에 정의에 의해 반드시 거짓이므로 'x가 공집합에 포함된다면 x가 A에 포함된다'는 반드시 참이다.
따라서 그러한 x는 존재하지 않는다.
그러므로 공집합이 있고, 공집합을 부분집합으로 가지지 않는 집합 A가 존재한다라고 가정이 모순이고 따라서 공집합은 모든 집합의 부분집합이다.
3)'p이면 q이다'가 참인 것과 동치는, p의 진리집합이 P이고 q의 진리집합이 Q일때, P가 Q의 부분집합이다라는 것이다.
p가 항상 참이고 q가 항상 참이면, p의 진리집합과 q의 진리집합은 U로 동일하고 U는 U의 부분집합이므로 P가 Q의 부분집합
p가 항상 참이고 q가 거짓이면, p의 진리집합은 U이고 q의 진리집합은 공집합이고, U는 공집합의 부분집합이 아니므로, P는 Q의 부분집합이 아니다.
p가 거짓이고, q가 참이면, p의 진리집합은 공집합이고, q의 진리집합은 U이므로, 공집합은 U의 부분집합이니까, P는 Q의 부분집합이다.
p가 거짓이고, q가 거짓이면, p의 진리집합은 공집합이고, q의 진리집합은 공집합이므로, 공집합은 공집합의 부분집합이니까 P는 Q의 부분집합이다.
따라서 'p이면 q이다'가 참인 것과 P가 Q의 부분집합이다는 동치이다.
4. 논리학적 설명
4-1) p → q의 정의
'p이면 q이다'의 논리학적 설명은 "If the first part is true, the second part must be true as well"
한국어로 번역하면, 'p가 참이면 q는 반드시 참이다', 즉 논리학에서는 p가 참인 경우에 대해서만 논한다
한국어로 p이면 q이다라고 할 때
p: '나는 배가 고프다'(I am hungry)
q: '나는 무엇인가를 먹고싶다'(I want to eat something)
p이면 q이다
한국어: '만약 내가 배가 고프면 나는 무엇인가를 먹고 싶다'
영어: "If i am hungry, then I want to eat something"
번역이 잘 된것 같지만 '만약 내가 배가 고프면 나는 무엇인가를 먹고 싶다'을 보면,
1)미래에 내가 배가 고프면 무엇인가를 먹고싶다라고 생각하게 된다.
하지만 논리학적 정의에 의해 명확하게 번역한다면,
"만약 '나는 배가 고프다'가 참이라면, 반드시 '나는 무엇인가를 먹고 싶다' 또한 참이다"
2)내가 배가 고프기 때문에 무엇인가를 먹고 싶다고 생각하게 된다.
인과관계가 있다고 생각하게 드는 이유는 그런 예시를 들었기 때문이다.
다른 예시로
p: 오늘 집 앞 옷가게가 11시에 문을 닫는다.
q: 나는 무엇인가를 먹고 싶다.
p와 q 사이 인과관계가 전혀 없어보이지만 p → q의 논리학적 정의에 맞춰 써보면
"만약 '오늘 집 앞 옷가게가 11시에 문을 닫는다'가 참이라면, 반드시 '나는 무엇인가를 먹고 싶다' 또한 참이다"
p와 q의 인과관계가 전혀 없어보이지만 위와 같이 만든 문장은 참일수도 있고 거짓일수도 있다
예를 들어 오늘 옷가게가 11시에 문을 닫았을 때 마침 내가 무엇인가를 먹고 싶었다면 위 문장은 참이다.
오늘 옷가게가 11시에 문을 닫았을 때, 내가 30분전에 과식을 우연히 해서 무언가를 먹고 싶지 않았다면 거짓이다.
이렇게 인과관계가 없더라도 명확하게 우리는 참, 거짓을 설명할 수 있다.
참, 거짓을 판단할 수 있는 문장이 명제이고 각 조건의 인과관계가 아니라, 오직 전체 문장의 참, 거짓을 판단할 수 있느냐는 관점으로 다가가야한다.
하지만 예시에서 '옷가게가 11시에 문을 닫지 않았다'라는 전제가 거짓일 때를 설명하지 못했지만,
그럼에도 논리학에서는 전제가 거짓일 때 조건문을 참이라고 하고 이를 공허참(vacuous truth)이라고 한다. 왜 이렇게 정의했냐면, 뒤의 p⇔q의 정의와 맞게 하기 위해서이다.
4-2) q→p의 정의
p: 오늘 집 앞 옷가게가 11시에 문을 닫는다.
q: 나는 무엇인가를 먹고 싶다.
다시 위 예시를 'p이면 q이다'의 논리학적 정의에 맞게 q→p에 맞춰서 써본다면
"만약 '나는 무엇인가를 먹고 싶다'가 참이라면, 반드시 '오늘 집 앞 옷가게가 11시에 문을 닫는다' 또한 참이다"
당장 알 수 있는 것은 p→q가 참이라고 q→p 가 반드시 참이 아니라는 것도 덤이다.???? 이걸로 어떻게 알아 어이없네
'내가 무엇인가를 먹고 싶을때, 때마침 옷가게가 11시에 문을 닫았으면 참이다.
'내가 무엇인가를 먹고 싶을때, 옷가게가 12시까지도 문을 열고 있으면 거짓이다.
4-3) p⇔q의 정의
“p이면 q이다.”라는 명제와 “q이면 p이다.”라는 두 명제가 있다고 하자. 이 두 명제를 합해 보면 우리에게 익숙한 “p이면 q이고, q이면 p이다,”라는 명제가 나오게 된다. 즉, 수학에서 말하는 필요충분조건이 된다. 이것을 논리학에서는 쌍조건문이라고 한다.
"p if and only if q"이고 논리학적 설명은 "If one is true, then the other is true; if one is false, then the other is false"
만약 'p가 참이라면 q도 참이고, p가 거짓이면 q도 거짓이다.'
마찬가지로 '만약 q가 참이라면, p도 참이고, q가 거짓이라면 p도 거짓이다.'
p,q의 참,거짓이 서로 같으면 p⇔q가 참이지만 서로 다르면 거짓이다?
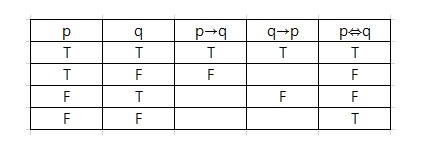
지금까지 우리가 논의한 3가지 명제에 대해서 p,q의 참 거짓에 따라 생각할 수 있는 부분을 보면 위와 같다
이제 공백을 채우기 위해 논리학적인 설명을 보면
p→q: "If p then q"
q→p: "If q then p"
p⇔q: "p if and only if q" 이것은 "If p then q and If q then p"이다.
여기서 주목할 부분은 p⇔q 연산은 p→q, q→p의 and 연산이라는 것을 알 수 있다
여기서 위 표에서 공백을 모두 거짓이라고 정의하고 and 연산을 모두 수행해서 정의와 비교해보면
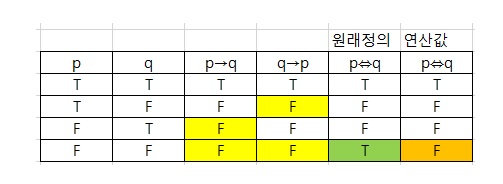
위의 경우 정의와 and연산값이 서로 다르다.
그런데 반대로 모두 참이라고 정의하고 and 연산을 수행해서 정의와 비교해보면

드디어 p⇔q의 정의 "만약 p가 참이라면 q도 참이고, 만약 q가 거짓이면 p도 거짓이다"와 p⇔q 연산은 p→q, q→p의 and 연산 둘 다 같은 값을 나타내게 된다.
이러한 이유로 우리는 "p이면 q에서 가정, 전제가 거짓일 때 조건문(p→q)이 항상 참"이라고 말할 수 있게 된 것이다.
5. 진리표

1)p가 거짓이면 q에 무관하게 p이면 q이다는 반드시 참이고
2)q가 참이면 p에 무관하게 p이면 q이다는 반드시 참
3)p이면 q이다가 거짓일려면 반드시 p가 참이고 q가 거짓이어야한다.
6. 출처
https://prudens-ripple.tistory.com/81
가정이 거짓이면 항상 참인 명제(집합을 이용하여 설명)
가정이 거짓이면 항상 참인 명제(집합을 이용하여 설명) 집합론과 논리학을 처음 배우는 사람들에게 가정 헷갈리는 내용 중 하나로 가정이 거짓이면 결론의 참, 거짓이 상관없이 명제는 항상 참
prudens-ripple.tistory.com
https://hoohaha.tistory.com/71
p이면 q에서 가정, 전제가 거짓일 때 조건문이 항상 참인 이유
진리표를 공부하다 p→q에서 쉽게 이해하기 어려운 부분이 있었다. 바로 p→q에서 전제(p)가 거짓일 때 조건문(p→q)가 항상 참이라는 것이다. 누구는 이것을 공허참(vacuous truth)으로 설명하고 누구
hoohaha.tistory.com
'프로그래밍 > 프로그래밍 개론' 카테고리의 다른 글
| 증명하기 연습문제3 (0) | 2022.09.15 |
|---|---|
| 증명하기 연습문제2 (0) | 2022.09.15 |
| 귀류법과 수학적 귀납법 정확히 알기 (0) | 2022.07.13 |
| 논리학 연습문제1 (0) | 2022.07.12 |
| hard logic과 soft logic의 차이 - 프로그래밍 언어에서 논리의 중요성 (0) | 2022.07.11 |

