1. 증명
19세기 말부터 증명이 무엇인지 많은 연구가 있었다
증명은 글로 쓰는 것이 아니라 '정확한 명제로 표현할 수 있는 것'이라는 것이 확립된 상태
보통 정확한 명제식으로 쓰지는 않지만 근본적으로는 명제식으로 바꿀 수 있는 것이 증명이다
증명에 대한 수많은 오해는 p ↔ q <p,q의 진리값이 같다> 와 p → q를 혼동하는 것에서 시작함
2. 당구공 paradox
'모든 당구공은 색이 같다'에 대한 증명
당연히 색이 같을리 없지만 논리적으로 증명하고자 함
------------------------------------------------------------------------------------------------------------
수학적 귀납법) 모든 자연수 n에 대해 명제 P(n)이 참이라는 것을 증명하기 위해서 2가지를 증명하면 된다
P(1)이 참
1이상의 자연수 k에 대하여 P(k)가 참이라고 가정하면, P(k+1)이 참이다
그러면 P(n)은 모든 자연수 n에 대해 참이다
------------------------------------------------------------------------------------------------------------
모든 자연수 n에 대해 당구공 n개가 들어있는 집합에서 그 집합에 포함된 당구공은 모두 색이 같다는 것을 증명하고자함
어떠한 n개의 당구공 집합을 만든다면 그 집합 내에서 당구공들은 모두 색이 같다
1) P(1): 당구공 1개가 들어있는 집합은 1개가 들어있으니까 당연히 집합 내의 모든 당구공은 색이 같다
2) 1이상의 자연수 k에 대하여 P(k)가 참이라고 가정하자. 당구공 k+1개가 들어있는 집합을 생각하자.
이러한 집합에서 당구공 1개를 빼보면..?

먼저 A를 하나 빼면 P(k)가 참이므로, 나머지 당구공들은 색이 같다
다시 A를 넣고 다른 B를 빼보면, P(k)가 참이므로, 나머지 당구공들은 색이 같다.
다시 B를 넣으면, A와 C는 색이 같고, B와 C도 색이 서로 같으므로, A와 B는 색이 같을 수밖에 없다
그러므로 k개의 당구공들이 서로 색이 같다는 P(k)가 참이면, k+1개의 당구공들이 서로 색이 같다는 P(k+1)이 참이다.
그렇지만 결과가 말이 안된다. 10개의 당구공 집합 아무렇게나 만들면 이들이 서로 색이 같을리가 없거든
반론1) P(n)이 참일리가 없다
이런 상황에서 대부분은 P(n)을 왜 참이라고 가정하냐고 반론한다
P(n)이 진짜 참인지 모르는데 왜 사실이라고 생각하느냐
하지만 수학적 귀납법에서 증명하려고 하는 것은 P(n)이 진짜로 참인지가 아니다
P(n)이 참이면, P(n+1)이 참이다라는 것을 보이는 것이 수학적 귀납법이다
즉 P(n) → P(n+1)을 증명하고자 하는것.
이미 우리는 P(n)이 거짓이면 P(n) → P(n+1)이 반드시 참이라는 것을 알고 있다
그러므로 P(n)이 정말로 참인지는 생각할 필요가 없다
P(n)이 정말로 사실인지 알아야 증명할 수 있다면
사실 수학적 귀납법의 목표는 P(n)이 정말로 참인지를 증명하는 것이 목표이기 때문에 수학적 귀납법 자체가 의미가 없다
-------------------------------------
사실 위 당구공 paradox에서 잘못된 것은
사실 k+1개의 당구공 집합에서 처음 뺀 당구공과 두번째로 뺀 당구공의 색이 정말로 같은지를 증명할 수가 없다는 것이다
즉 P(1)이 참인것은 명백한데 당구공이 2개만 들어있는 집합을 생각해보면

A를 빼면 B가 1개 있으니까 당구공 집합내의 당구공들이 서로 색이 같고
A를 넣고 B를 빼면 A가 1개 있으니까 당구공 집합내의 당구공들이 서로 색이 같지만
결국 A와 B가 색이 같은지는 알수가 없다
즉 P(2)에서는 성립하지 않는다.
이러한 증명이 오해를 불러일으킨 부분은 처음에 당구공 집합을 그릴때 당구공의 수가 매우 많다는 것 때문에
처음에 넣고 뺀 2개의 당구공도 색이 괜히 같을 것이라는 착각을 불러일으킨다
3. 소수의 수는 무한히 많다
prime의 수가 유한한 k개라고 가정하고 $p_{1}, p_{2}, p_{3},... , p_{k}$라고 쓸 수 있다
그러한 모든 prime을 곱하고 1을 더한 수를 n이라고 하자
$$n = p_{1}p_{2}...p_{k}+1$$
그러면 이 n은 가장 큰 prime보다 큰 수라고 할 수 있다
즉 prime이 아니다. 유한한 k개라고 가정했으니까
prime이 아닌 수는 소인수분해가 가능해야한다
---------------------------------------------------------------
1보다 큰 모든 자연수는 소수이거나 합성수이다.
합성수는 소수가 아닌 수이다.
합성수는 약수의 개수가 3개 이상이고 둘 이상의 소수를 곱한 수이다
합성수는 소수들의 곱으로 나타낼 수 있으며 이를 소인수분해라고 부른다
-----------------------------------------------------------------------------
따라서 n은 어떠한 prime으로 나누어 떨어져야한다. 왜냐하면 1보다 크면서 소수가 아닌 수이니까
그러나 이 n은 존재하는 모든 prime $p_{1}, p_{2}, p_{3},... , p_{k}$으로 나누더라도 반드시 나머지가 1이다
즉, 나누어 떨어지는 경우가 없다
이는 모순되므로 prime은 유한하지 않고 무한히 많다
제대로 된 증명이지만 가끔 반론이 나온다
반론) 몇개의 prime이 더 있으면 되는거 아님?
즉, 무한하다는 것이 증명된 것이 아니라 k개보다 많다는 것만 증명되었을 뿐이다
방금 만든 n을 나누어 떨어뜨리는 어떤 prime $p_{k+1}$이 존재하기만 하면 모순이 해소된다
---------------------------------------
하지만 우리가 증명한 것은 'prime이 k개이면 모순이 발생'을 증명한 것인데
이는 명제로 바꿔쓰면 모순은 항상 거짓이므로 'prime이 k개이다 → 항상 거짓'이라는 명제가 참임을 증명한 것이다
그런데 q가 항상 거짓인데 p → q가 참이라면 p가 반드시 거짓이어야한다.
즉 'prime이 k개이다' 라는 것은 모든 k에 대해 반드시 거짓이다
따라서 prime은 무한히 많다
4. 수학적 귀납법이란
컴퓨터 알고리즘은 수학적 귀납법으로 증명되는 경우가 상당히 많다
수학적 귀납법의 기본형태)
1)P(1)이 참이다
2)1이상의 자연수 n에 대하여 P(n)이 참이라면, P(n+1)이 참이다.
1), 2)가 모두 참이면 모든 자연수 n에 대해 P(n)이 참이다
------------------------------------------------
수학적 귀납법의 강한형태)
1) P(1)이 참이다.
2) P(1), P(2), P(3), ..., P(n)이 모두 참이라면, P(n+1)이 참이다.
1), 2)가 모두 참이면 모든 자연수 n에 대해 P(n)이 참이다.
--------------------------------------------------
강한 형태가 당연히 더 증명하기가 쉽다. 기본형은 P(n)이 참이라고 가정하지만 강한형태는 가정이 P(1), P(2), P(3), ..., P(n)이 모두 참으로 더 많다
기본형태와 강한형태는 둘이 동치이지만, 강한형태가 뭔가 조건이 더 많아 쓰기 어려워보인다
하지만 원래 기본형 P(n)이 참이라고만 가정한 것에서 P(1), P(2), ..., P(n)이 각각 참이다라고 잔뜩 가정하고
이들 중에서 자기가 원하는거 아무거나 몇개 골라쓰기만해도 패널티를 먹기는 커녕 수학적 귀납법과 동치라니 오히려 더 편하다?
5. 연습

x가 0이하이면 0을 return하고 아니면 x+sum(x-1)을 return하는 재귀적 함수
일반적으로는 S(n) = n + S(n-1)을 그대로 코딩한 것이므로 1부터 n까지의 합이 증명된 것이다라고 말한다
하지만 정확한 증명에 '답이 당연하다'라고 하는 것은 적절하지 않아
증명을 하려면 증명이 가능한 명제가 있어야함
합을 계산한다라는 것은 일상생활의 언어이므로 증명이 불가능함
hard logic으로 이를 바꿀필요가 있다
------------------------
증명이 가능한 명제: 'sum(x)가 return하는 값은 1+2+...+x와 항상 같다'
이러한 명제를 만들 수 있을까? 사실 쉽지 않다. 연습이 필요함
그러면 수학적 귀납법을 적용할 수 있음
1) P(1)이 참이다: 'sum(1)이 return하는 값은 1이다' 실제 코드도 sum(1)이 1을 return하므로 참
2) P(n)이 참이면, P(n+1)이 참이다
이것을 조금 trick하게 바꿔보면 P(n-1)이 참이면, P(n)이 참이다.와 동치임
그래서 'sum(x-1)이 return하는 값은 1+2+...+(x-1)과 같다'가 참이면, 'sum(x)가 return하는 값은 1+2+...+x와 같다'가 참이다
코드에서 sum(x)는 x+sum(x-1)을 return한다
그런데 sum(x-1)은 1+2+,..+(x-1)과 같다고 가정하고 있으므로, sum(x)는 x+(1+2+...+(x-1)) = 1+2+...+x를 return한다는 것이 참이다
-------------
6. 재귀함수 꿀팁
재귀함수에서 중요한 것이 sum(x-1)을 블랙박스로 보는 것이 중요하다?
많은 사람들이 sum(x)함수 보고 return값이 sum(x-1)이 있으니까 sum(x-1)이 어떤 일이 생겨날지 계속 생각하는 사람이 있는데..
그거 나인데?
sum(x-1)이 어떤 값을 return하는지 약속으로 정하고, 그 약속이 지켜진다고 가정하고,
똑같은 약속을 sum(x)에 적용하고 실제로 그 약속이 참인지만 확인해보면 된다
수학적 귀납법처럼.. sum(x-1)이 뭘 return하는지는 걱정할필요가 전혀 없고 진짜로 어떤 값을 return한다고 가정하고
그럴경우에 sum(x)가 제대로 된 값을 return하는지만 확인해보면 끝
이거 지리는데???
7. 귀류법(proof by contradiction)
어떤 명제가 참임을 가정한 후에 어떤 모순을 이끌어내 그 가정이 거짓임을, 즉 처음의 명제가 참이 됨을 간접적으로 증명하는 방법
논증(argument)
p
∴q
가 있다고 하자.
p는 전제(premise, hypothesis)이고 q는 결론(conclusion)이다.
모든 논증은 그에 상응하는 조건명제(conditional statement)로 바꿀 수 있다.
그러므로 위 논증은 조건 명제 p → q와 같다.
논증이 타당함을 보일려면 "전제 p가 참이면 결론 q가 참"임을 보여야 하지만 직접적으로는 추론이 어려운 경우가 많다
p → q와 논리적으로 동치인 명제는 항상 거짓인 모순명제 F에 대하여 다음과 같다.
p → q ≡ ~p ∨ q ≡ ~(p ∧~ q) ≡ ~(p ∧~ q) ∨ F ≡ (p ∧~ q) → F
진리표로 p → q ≡ ~p ∨ q이 동치임을 생각해보면
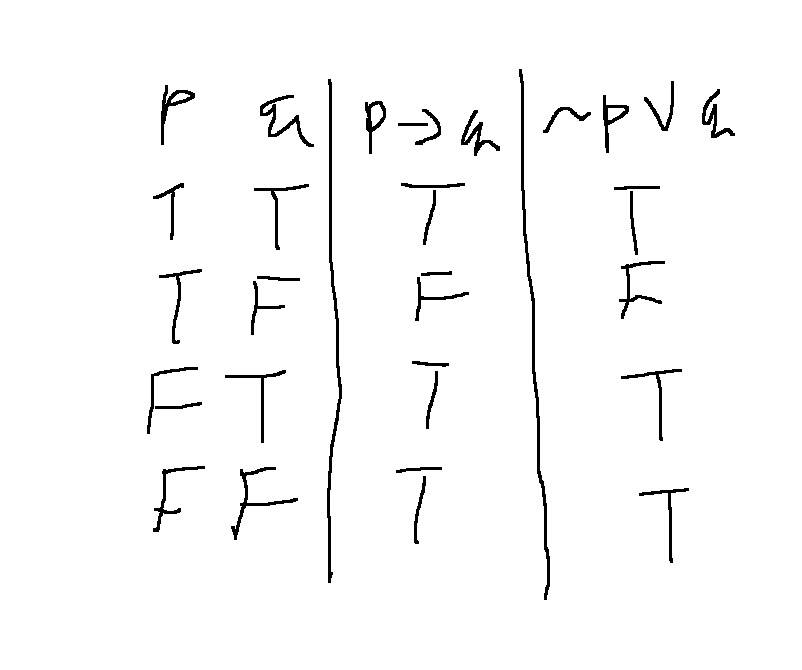
~p ∨ q ≡ ~(p ∧~ q)은 드모르간의 법칙에 의해 동치가 된다
~(p ∧~ q) ≡ ~(p ∧~ q) ∨ F은 F가 항상 거짓이므로, ~(p ∧~ q)이 T이면 ~(p ∧~ q) ∨ F은 T ∨ F로 T가 되고
~(p ∧~ q)이 F이면 ~(p ∧~ q) ∨ F은 F ∨ F로 F가 된다.
~(p ∧~ q) ∨ F ≡ (p ∧~ q) → F은 p → q ≡ ~p ∨ q에서 각각 p는 (p ∧~ q)이고 q는 F이면 된다
그래서 p → q와 (p ∧~ q) → F가 논리적으로 동치이다.
모든 조건명제는 그에 상응하는 논증으로 바꾸어 쓸수있다.
(p ∧~ q) → F에 상응하는 논증은
p
~q
∴F
명제 p → q의 결론 q를 부정하면 ~q가 되는데 이것을 다른 전제 p와 같이 전제로 가정하고,
즉 p and ~q라고 가정한 뒤에 어떤 논리적 과정을 거쳐서 모순명제 F를 이끌어낸다면,
p → q는 타당한 논증이다.
이것이 바로 귀류법이다.
사실

