1. skewness(왜도)
실수 값을 가지는 확률 변수의 분포가 평균을 기준으로 얼마나 비대칭적인지를 나타내는 척도
양수, 0, 음수 혹은 정의되지 않음이 될 수 있다
수학적으로 확률변수 X의 3차 표준화 적률이다.
$$E((\frac{X-\mu}{\sigma})^{3}) = \frac{1}{\sigma^{3}} E((X-\mu)^{3})$$
여기서 $\sigma^{2} = E((X-\mu)^{2})$이므로,
$$E((\frac{X-\mu}{\sigma})^{3}) = \frac{E(((X-\mu)^{3})}{E((X-\mu)^{2})^{3/2}}$$
표본 왜도는 다음과 같이 정의된다.
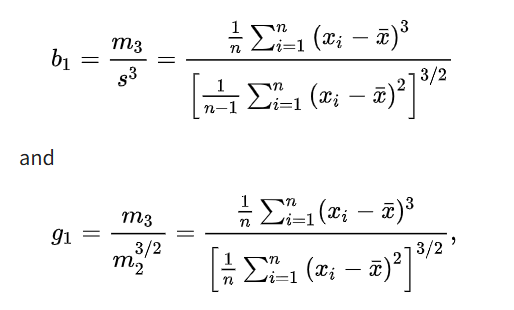
2. 왼쪽으로 치우친 분포와 오른쪽으로 치우친 분포
아래 그림의 확률 분포를 보면 첫번째 그림은 왼쪽 값들이 가늘어지고 있고 두번째 그림은 오른쪽 같들이 가늘어지고 있다
이렇게 분포에서 점점 가늘어지는 부분을 꼬리(tail)라고 부른다

1) 왼쪽으로 치우친 분포(skewed to the left)
왼쪽으로 꼬리가 길고, 분포의 대부분이 오른쪽에 집중되는 분포를 negative skew라고 부른다.
즉 왜도가 음수이다.
이러한 분포를 왼쪽으로 왜곡되어 있다(left skewed), 왼쪽 꼬리를 가진(left tailed), 왼쪽으로 치우친(skewed to the left) 분포라고 말한다.
곡선 자체는 오른쪽으로 기울어져있는데, 왼쪽으로 치우친 분포라고 부르는 것에 주의하라.
이는 평균값이 중앙값보다 왼쪽으로 치우쳐진 경우가 많다.
2) 오른쪽으로 치우친 분포(skewed to the right)
오른쪽 꼬리가 더 길고, 분포의 대부분은 왼쪽에 집중되어 있는 분포를 positive skew라고 부른다.
이러한 분포는 오른쪽으로 왜곡되어있다(right skewed), 오른쪽 꼬리를 가진(right tailed), 오른쪽으로 치우쳤다(skewed to the right)라고 부른다.
역시 곡선 자체는 왼쪽으로 기울어져있지만, 오른쪽으로 치우친 분포라고 부르는 것에 주의하라.
이는 평균값이 중앙값에 비해 오른쪽에 치우쳐진 경우가 많다.
3. 왜도에 대한 오해
봉우리가 mode(최빈값)를 나타내고.. 중간이 median이며 다른쪽이 mean
일반적으로 왜도가 양수면 왼쪽 그림처럼 최빈값 < 중앙값 < 평균
왜도가 음수면 평균 < 중앙값 < 최빈값
왜도가 0이면 평균 = 중앙값 = 최빈값

그러나 왜도는 평균, 중앙값간의 관계와 직접적으로 연결되어 있지 않다.
이전의 비모수적 왜도(nonparametric skewness) 개념에서는
$$\frac{\mu - \nu}{\sigma}$$로 정의되었다.
$\mu$는 평균이고 $\nu$는 중앙값 $\sigma$는 표준편차이다.
이에 따르면 왜도가 양수면 평균 > 중앙값, 음수면 평균 < 중앙값이고 왜도가 0이면 평균 = 중앙값이다.
하지만 현대적인 모멘트 기반의 정의 $$E((\frac{X-\mu}{\sigma})^{3})$$에서는 이것이 항상 성립하지는 않는다.
분포가 대칭이라면 평균 = 중앙값이고 이때 왜도는 0이다.
분포가 대칭이면서 단봉(unimodal)이라면 평균 = 중앙값 = 최빈값이다.
하지만 그 역은 일반적으로 성립하지 않는다.
즉, 왜도가 0이라고 해서 반드시 평균과 중앙값이 같지는 않다.
다봉 분포(multimodal)나 한쪽 꼬리는 길지만 다른 쪽 꼬리는 무거운 분포,
이산 분포에서 중앙값을 기준으로 왼쪽, 오른쪽의 면적이 동일하지 않은 경우 잘 작동하지 않는다

위 분포는 왜도가 양수이지만, 평균이 중앙값, 최빈값의 왼쪽에 있다.
38%가 중앙값의 왼쪽에 있고, 49%는 중앙값과 일치하고, 13%는 중앙값의 오른쪽에 존재한다.
평균은 더 무거운 왼쪽에 위치하지만, 더 긴 오른쪽 꼬리가 왜도가 양수임을 말해주고 있다.
연속형 확률 분포는 위반되는 경우가 적지만 충분히 위반되는 경우가 존재할 수 있다
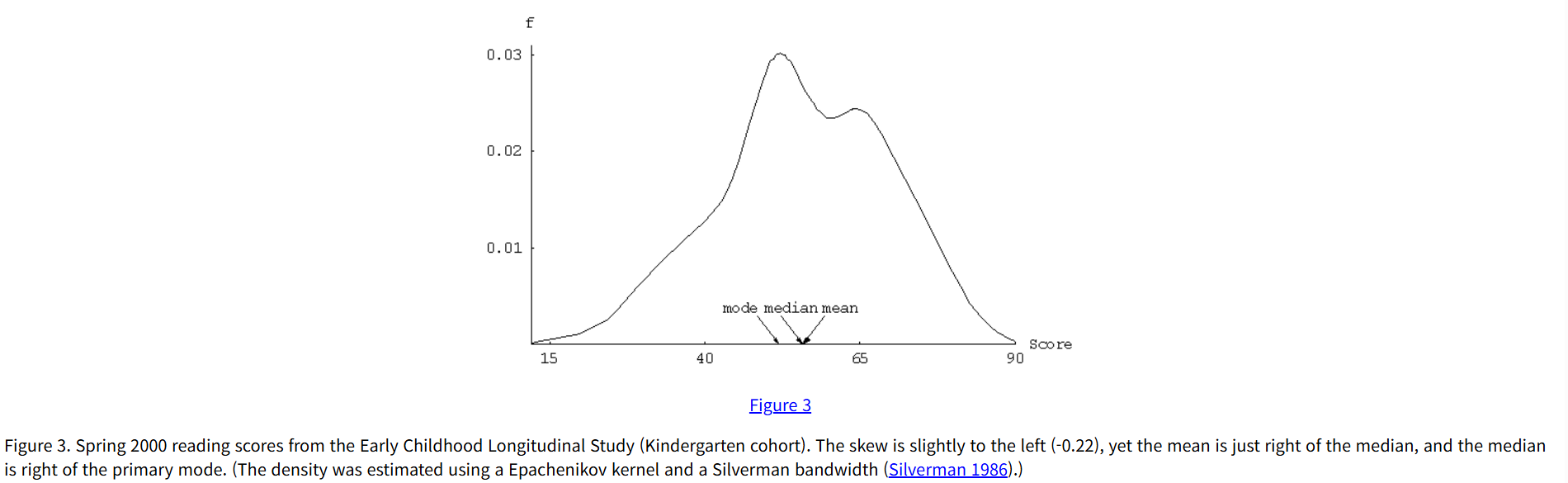
이론적인 분포도 충분히 위반되는 경우가 존재할 수 있다
이산형 분포중 포아송분포의 경우 $\mu = 0.75$인 경우 왜도가 양수이지만 평균은 중앙값의 왼쪽에 있다
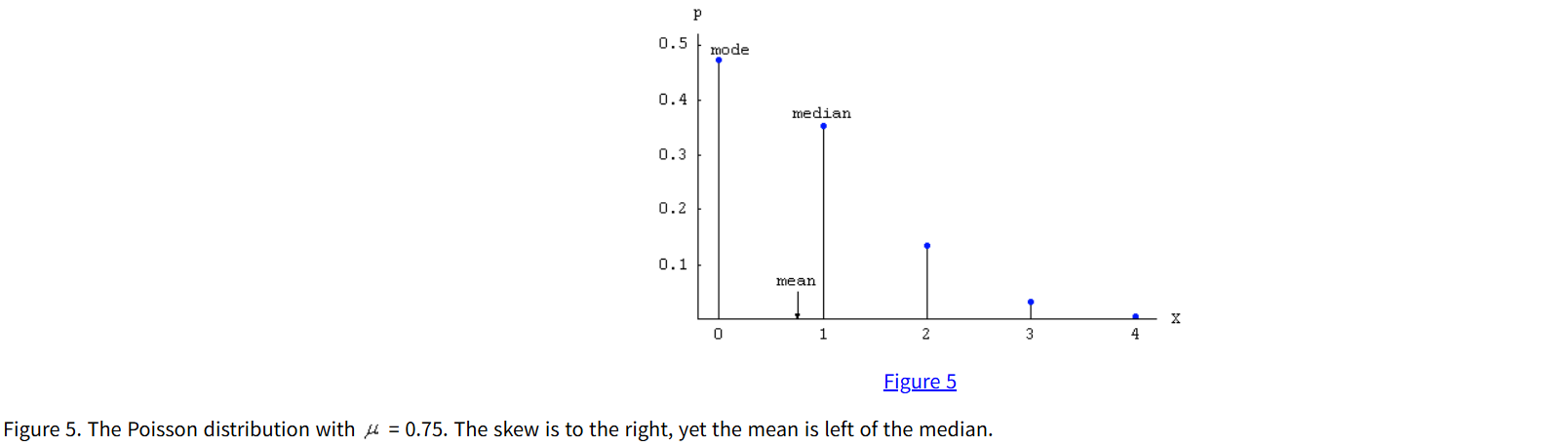
다봉우리 연속 분포는 위반되는 경우가 종종 있고, 단봉우리 연속 분포는 보통은 위반되는 경우가 없지만
다음과 같은 웨이불 분포분 왜도가 양수지만 중앙값의 왼쪽에 평균이 있다

Journal of Statistics Education, v13n2: Paul T. von Hippel
web.archive.org
'다시보는 통계학' 카테고리의 다른 글
| 일반화된 몬티 홀 문제(monty hall problem) (0) | 2025.05.10 |
|---|---|
| 가중 절댓값 합(weighted absolute sum)을 최소로 만드는 방법(subgradient optimization) (0) | 2025.05.07 |
| feature scaling을 위한 정규화(normalization) 기법들 (0) | 2025.04.12 |
| 상관관계는 인과관계가 아니다 - confounder model(교란변수 모델) (0) | 2024.04.20 |
| 조건부확률과 베이즈정리 이론 간단하게 (0) | 2024.01.04 |

