1. 가중 절댓값 합(weighted absolute sum)
$$f(x) = \sum_{i = 1}^{n} w_{i} | x - a_{i} | $$을 최소로 만드는 x는 무엇일까
잘 알지만 $f(x) = |x|$는 미분 불가능한 함수이다.
최적화를 위해서는 subgradient에 대해 알아야한다.
https://hgmin1159.github.io/convex/firstorder2/
[First-Order Method] Part2. Subgradient Method
Subgradient Method
hgmin1159.github.io
여기가 설명이 잘 나와있긴 한데 어렵다
대충 일단 $f(x) = |x|$는 x > 0, x < 0에 대해서 f(x) = x, f(x) = -x이고 이를 미분하면 f'(x) = 1, f'(x) = -1로 미분가능인데
x = 0에서는 미분 불가능이다.
그래서 subgradient를 f'(x) = 1 ( x > 0), f'(x) = [-1,1] (x = 0), f'(x) = -1 ( x < 0)로 정의
x = 0에서 기울기는 [-1,1]사이 아무 값이나 될 수 있다는 그런 뜻?
그리고 최적화 조건은
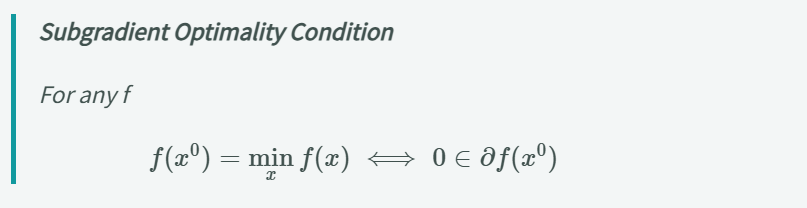
subgradient에 0이 포함되어야한다
이에 맞춰서 한번 미분을 해보자
$$ \frac{df(x)}{dx} = \sum_{x > a_{i}}^{} w_{i} + \sum_{x < a_{i}}^{} -w_{i} + \sum_{x = a_{i}}^{} [-w_{i},w_{i}] $$
따라서 다음과 같이 f(x)의 subgradient는
$$\partial f(x) = [ \sum_{x > a_{i}}^{} w_{i} - \sum_{x < a_{i}}^{} w_{i} - \sum_{x = a_{i}}^{} w_{i}, \sum_{x > a_{i}}^{} w_{i} - \sum_{x < a_{i}}^{} w_{i} + \sum_{x = a_{i}}^{} w_{i} ]$$
최적화 조건은 이 구간 안에 0이 포함되어야한다.
$$L = \sum_{x > a_{i}}^{} w_{i} - \sum_{x < a_{i}}^{} w_{i} - \sum_{x = a_{i}}^{} w_{i}$$
$$R = \sum_{x > a_{i}}^{} w_{i} - \sum_{x < a_{i}}^{} w_{i} + \sum_{x = a_{i}}^{} w_{i}$$
라고 하면 [L,R] 구간에 0이 들어있어야하므로, L <= 0 <= R이다.
L <= 0이라는 것은
$$\sum_{x > a_{i}}^{} w_{i} - \sum_{x < a_{i}}^{} w_{i} - \sum_{x = a_{i}} w_{i} <= 0$$
전체 합 $W = \sum_{i = 1}^{n} w_{i}$라고 하자.
$\sum_{x > a_{i}}^{} w_{i} = W - (\sum_{x < a_{i}}^{} w_{i} + \sum_{x = a_{i}}^{} w_{i})$이므로
$W - 2( \sum_{x < a_{i}}^{} w_{i} + \sum_{x = a_{i}}^{} w_{i}) <= 0$ 이 된다.
따라서, $$\frac{W}{2} <= \sum_{x <= a_{i}}^{} w_{i}$$
반대로 0 <= R이라는 것은
$$0 <= \sum_{x > a_{i}}^{} w_{i} - \sum_{x < a_{i}}^{} w_{i} + \sum_{x = a_{i}}^{} w_{i}$$
$\sum_{x < a_{i}}^{} w_{i} = W - (\sum_{x > a_{i}}^{} w_{i} + \sum_{x = a_{i}}^{} w_{i})$이므로,
$W <= 2(\sum_{x > a_{i}}^{} w_{i} + \sum_{x = a_{i}}^{} w_{i})$이다.
따라서, $$\frac{W}{2} <= \sum_{x >= a_{i}}^{} w_{i}$$
그러므로 $$\frac{W}{2} <= \sum_{x >= a_{i}}^{} w_{i} 이고 \frac{W}{2} <= \sum_{x <= a_{i}}^{} w_{i}$$를 만족하는 $x = a_{i'}$이다.
2. 연습문제
마을의 좌표 a1,a2,a3,...,an이 주어지고 이 마을 중 한 마을에 경기장을 지을려고 한다.
각 마을에 사는 사람의 수 w1,w2,...,wn이 주어진다.
각 사람이 경기장까지 가는 거리의 합을 최소로 하는 지점에 경기장을 짓고 싶다.
그 경기장의 좌표는?
-------------------------------------------------------------------------------------------------------------------------------------------
경기장을 지을려는 좌표를 x라고 한다면, 문제에서 원하는 값은
$\sum_{i = 1}^{} w_{i} | x - a_{i} | $를 최소로 하는 x값을 구하는 것이다.
따라서 위에서 배운 가중 절댓값 합을 최소로 하는 x값을 찾으면 된다.
가중치의 총합을 W라고 한다면, 어떤 지점 x = A[i]에 대하여 이 지점을 포함한 왼쪽 합 $\sum_{x <= A[i]}^{} w_{i}$가 W/2이상이면서,
오른쪽 합 $\sum_{x >= A[i]}^{} w_{i}$가 W/2가 되는 가장 작은 x값을 찾으면 된다.
왼쪽 합과 오른쪽 합을 O(1)에 구하기 위해 가중치 배열 B의 누적합 배열을 미리 구해놓는다면, 정답을 O(N)에 찾을 수 있다
from sys import stdin
T = int(stdin.readline())
for _ in range(T):
n = int(stdin.readline())
A = list(map(int,stdin.readline().split()))
B = list(map(int,stdin.readline().split()))
for i in range(1,n):
B[i] += B[i-1]
W = B[-1]
for i in range(n):
x = A[i]
v1 = B[i]
if i == 0:
v2 = B[n-1]
else:
v2 = B[n-1] - B[i-1]
if v1 >= W/2 and v2 >= W/2:
answer = x
break
print(answer)
근데 사실 왼쪽 합 $\sum_{x <= A[i]}^{} w_{i} >= W/2$를 만족하는 가장 작은 x를 찾으면 된다.
그러니까 오른쪽 합은 검사하지 않아도 되는데, 왜 그런지 알아보자.
편의를 위해서 다음과 같이 정의하자.
$L = \sum_{x < a_{i}}^{} w_{i}, E = \sum_{x = a_{i}}^{} w_{i}, R = \sum_{x > a_{i}}^{} w_{i}$
그러면 L + E + R = W이다.
만약 L <= W/2이면, R+E >= W/2임을 알 수 있다.
왜냐하면 L <= W/2이면, L = W - R - E이므로, W - R - E <= W/2이므로 W/2 <= R+E
따라서, L <= W/2이면, R+E >= W/2이다.
그러므로 v = 0부터 시작하고 i = 0,1,2,..,n-1까지 B 배열의 왼쪽부터 누적해서 v에 더해가자.
이때 어떤 지점 x = A[i]에서 w값을 v에 더했더니, v >= W/2를 만족한다는 것은 무엇을 뜻하는가?
v에는 왼쪽 합 L이 구해지고 있었는데, L+E >= W/2를 만족하게 된다는 뜻이다.
그러니까 L <= W/2였는데, 어느 순간 E값을 더했더니 처음으로 L+E >= W/2가 된다는 뜻이다.
그러면 L <= W/2이므로, R+E >= W/2가 된다.
따라서, 왼쪽부터 가중치를 누적하다가 그 합이 W/2 이상이 된다면 자동으로 그 지점을 포함한 오른쪽 합도 W/2이상이 된다.
from sys import stdin
T = int(stdin.readline())
for _ in range(T):
n = int(stdin.readline())
A = list(map(int,stdin.readline().split()))
B = list(map(int,stdin.readline().split()))
W = sum(B)
v = 0
for i in range(n):
x = A[i]
v += B[i]
if v >= W/2:
answer = x
break
print(answer)
'다시보는 통계학' 카테고리의 다른 글
| 일반화된 몬티 홀 문제(monty hall problem) 2 (0) | 2025.05.12 |
|---|---|
| 일반화된 몬티 홀 문제(monty hall problem) (0) | 2025.05.10 |
| 왜도(skewness)에 대한 오해 - 오른쪽으로 치우친 분포와 왼쪽으로 치우친 분포? (0) | 2025.04.21 |
| feature scaling을 위한 정규화(normalization) 기법들 (0) | 2025.04.12 |
| 상관관계는 인과관계가 아니다 - confounder model(교란변수 모델) (0) | 2024.04.20 |

