1. 왜 해야하는가?
원본 데이터의 값 범위가 크게 다를 경우, 일부 머신러닝 알고리즘에서는 정규화를 하지 않으면 목적 함수가 제대로 작동하지 않을 수 있습니다.
예를 들어, 많은 분류기(classifier)들은 두 지점 간의 유클리드 거리(Euclidean distance)를 계산합니다.
만약 어떤 특성(feature)이 매우 넓은 값의 범위를 가진다면, 이 거리 계산은 해당 특성에 의해 지배될 수 있습니다.
따라서 모든 특성의 값 범위를 정규화하여, 각 특성이 최종 거리 계산에 거의 비슷한 비중으로 기여하도록 하는 것이 중요합니다.
또한, 정규화를 적용하는 또 다른 이유는 경사 하강법(gradient descent)이 정규화를 통해 훨씬 더 빠르게 수렴하기 때문입니다.
정규화는 손실 함수에 정규화 항(regularization)이 포함된 경우에도 중요합니다.
이때는 각 계수가 적절하게 패널티를 받을 수 있도록 하기 위해 정규화를 적용해야 합니다.
경험적으로도, 특성 정규화는 확률적 경사 하강법(Stochastic Gradient Descent)의 수렴 속도를 향상시킬 수 있습니다.
서포트 벡터 머신(Support Vector Machine, SVM)에서도 정규화를 통해 서포트 벡터를 찾는 시간을 줄일 수 있습니다.
또한, 데이터 간의 거리나 유사도를 기준으로 하는 작업들 — 예를 들어 클러스터링(clustering)이나 유사도 검색(similarity search) — 에서도 정규화는 자주 사용됩니다.
예를 들어, K-평균(K-means) 클러스터링 알고리즘은 특성들의 스케일에 민감하기 때문에 정규화가 특히 중요합니다.
2. 최대 - 최소 정규화(min max normalization)
$$\frac{x - min(X)}{max(X) - min(X)}$$로 정규화 하는 기법
모든 데이터의 범위를 [0,1] 내로 들어오게 한다.
이상치에 약하다는 특징이 있다.
간단하게 생각해보면 이상치는 1에 가까워지고, 그 외의 데이터는 0에 가까워지니까
만약 [a,b] 범위 내로 들어오게 하고 싶다면
$$a + \frac{(x - min(X))(b-a)}{max(X) - min(X)}$$
3. 평균 정규화(mean normalization)
$$\frac{x - mean(X)}{max(X) - min(X)}$$로 정규화하는 기법
4. 표준화(standardization)
다양한 유형의 데이터의 각각 feature의 평균을 0, 표준편차를 1로 만드는 기법
$$\frac{x - mean(X)}{std(X)}$$
평균 정규화에서 분모를 max(x) - min(x)에서 std(x)로 바꾼 것
많은 머신러닝 알고리즘에서 주로 사용
5. Robust scaling
중앙값과 사분위수 범위를 이용하여 정규화하는 기법
이상치에 강하다는 특징이 있다.
Q2(x)는 중앙값, Q3(x)는 제 3 사분위수 Q1(x)는 제 1 사분위수 일때,
$$\frac{x - Q2(X)}{Q3(X) - Q1(X)}$$
6. log transformation
오른쪽으로 치우친 분포(positive skewed)에 대해 사용하면 정규분포에 가깝게 정규화시켜준다고 알려진 기법
$$log(x)$$
만약에 x에 0이 포함되어 있다면, $$log(x + 1)$$로 하기도 한다
7. power transformation
Box - Cox transformation이나 Yeo - Johnson transformation은 비대칭 분포를 정규분포에 가깝게 변환시키는 방법
다음은 box cox transformation이고 양수에만 사용 가능하다
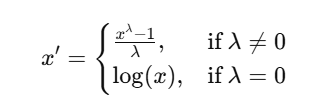
scipy.stats의 boxcox로 사용가능
from scipy import stats
import numpy as np
import matplotlib.pyplot as plt
# 양수 데이터 생성 (예: 오른쪽으로 치우친 분포)
data = np.random.exponential(scale=2, size=1000)
# Box-Cox 변환 적용
transformed_data, lambda_ = stats.boxcox(data)
print(f"최적의 lambda 값: {lambda_}")
# 시각화
plt.figure(figsize=(12, 5))
plt.subplot(1, 2, 1)
plt.hist(data, bins=30, color='skyblue')
plt.title("원본 데이터")
plt.subplot(1, 2, 2)
plt.hist(transformed_data, bins=30, color='lightgreen')
plt.title("Box-Cox 변환된 데이터")
plt.tight_layout()
plt.show()
다음은 Yeo - Johnson transformation은 양수, 음수 모두에 사용가능하다

$\lambda$는 최대 가능도 추정법으로 찾는다는데
sklearn.preprocessing.PowerTransformer(method = 'yeo-hohnson')으로 사용가능
from sklearn.preprocessing import PowerTransformer
import numpy as np
import matplotlib.pyplot as plt
# 음수 포함한 데이터 생성
data = np.random.lognormal(mean=0.5, sigma=1.0, size=(1000, 1))
# Yeo-Johnson 변환 적용
pt = PowerTransformer(method='yeo-johnson')
transformed_data = pt.fit_transform(data)
print(f"최적의 lambda 값: {pt.lambdas_}")
# 시각화
plt.figure(figsize=(12, 5))
plt.subplot(1, 2, 1)
plt.hist(data, bins=30, color='salmon')
plt.title("원본 데이터")
plt.subplot(1, 2, 2)
plt.hist(transformed_data, bins=30, color='lightblue')
plt.title("Yeo-Johnson 변환된 데이터")
plt.tight_layout()
plt.show()
8. max abs scaling
데이터의 절댓값의 최댓값으로 나누는 기법
$$\frac{x}{max(abs(x))}$$
데이터의 가장 큰 값은 1이 되고, 데이터의 가장 작은 값은 0이 되므로, -1 ~ 1사이로 mapping된다.
0을 그대로 0으로 만드므로, sparse matrix에서 사용하면 좋지만 잘 쓰는 기법은 아님
9. 기타
제곱 변환, 제곱근 변환 등등도 가능한데, 로그 변환으로 대체 가능한듯?
데이터의 분포를 원하는 분포로 바꾸는 quantile transformation도 있다
https://deepdata.tistory.com/83
분위수 변환(quantile transformation)
1. quantile transformation의 이론적인 설명 주어진 데이터 $x _{1},x _{2} ,...,x _{n}$의 분포를 그려보니 다루기 힘들거나 마음에 안들어서 분포를 변환할 필요가 있다고 합시다. 주어진 데이터 $x _{1},x _{2}
deepdata.tistory.com
'다시보는 통계학' 카테고리의 다른 글
| 가중 절댓값 합(weighted absolute sum)을 최소로 만드는 방법(subgradient optimization) (0) | 2025.05.07 |
|---|---|
| 왜도(skewness)에 대한 오해 - 오른쪽으로 치우친 분포와 왼쪽으로 치우친 분포? (0) | 2025.04.21 |
| 상관관계는 인과관계가 아니다 - confounder model(교란변수 모델) (0) | 2024.04.20 |
| 조건부확률과 베이즈정리 이론 간단하게 (0) | 2024.01.04 |
| 통계적 모델링과 최대가능도추정법(Maximum likelihood estimation) 간단하게 (0) | 2024.01.03 |

