0. 개요
조건부확률은 두 변수간의 상관정도를 측정해주는 통계적 해석을 제공하지만 데이터가 충분히 많아지더라도 이것이 인과관계를 가진다고 추론할 수는 없다.
조건부확률에 기반한 모형은 보통 확률분포 변화에 민감하다
무슨말이냐면 훈련된 모형에서 정확도가 매우 높더라도 테스트 모형에서 분포(데이터)가 조금이라도 변하면 성능이 떨어질 수 있다.
인과관계에 기반한 예측모형은 테스트할 때 데이터의 변화에 강건하여 성능변화가 거의 없다

조건부확률은 교란변수(중첩요인,confounding factor)의 영향에 의해 높게 측정될 수 있다
예를 들어 키가 클 수록 지능지수가 큰 경향이 있는데 일반적으로는 무관하다는 것을 안다
데이터 분석하면 저런 경향이 나오는데 나이라는 변수의 영향이 있어서 그렇다.
두 변수에 동시에 영향을 미치는 요인의 효과를 제거한 조건부확률을 구하여 두 변수간 인과관계를 명확히 한 뒤에 사용하는 것이 좋다.

1. confounding factor
독립변수와 종속변수에 모두 영향을 미치는 변수이다.
특히 중요한 점은 confounding factor를 생각할 때는 상관관계나 연관관계의 측면에서 기술하지 않고 두 변수간 인과관계를 가정하고 기술한다
Confounding is a causal concept, and as such, cannot be described in terms of correlations or associations.
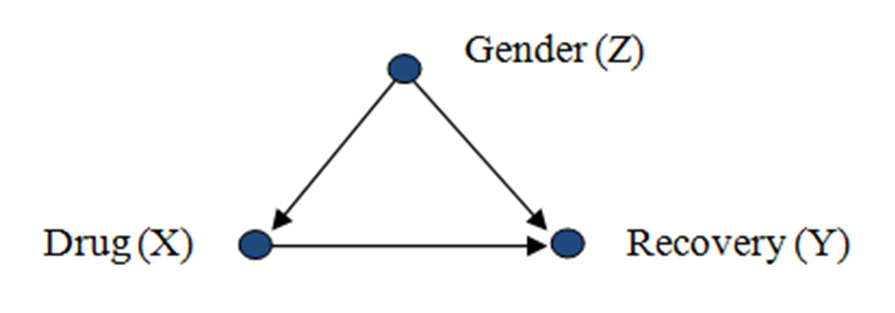
중요한 점은 X가 Y의 원인이라 생각하고 둘은 Z에 영향을 미치지 않는데 Z가 두 변수에 모두 영향을 미친다
그러니까 두 변수간 인과관계가 있다고 생각하는데
confounding factor가 두 변수에 모두 영향을 미쳐 spurious correlation을 만든다
spurious correlation은 허위적 상관관계
상관관계는 있지만 인과관계는 아닌 관계
위에서 나온 키가 클수록 지능지수가 큰 관계를 spurious correlation
이거는 confounding factor 나이에 의해 우연히 서로가 영향받은 상관관계이다
2.두 변수가 오직 서로만 영향을 미치는 인과관계란
독립변수 X와 종속변수 Y, confounder를 Z라고 한다.
여기서 P(Y|do(X))는 X를 직접 통제했을 때 Y가 일어날 조건부확률
이 때 두 변수가 Z에 의해 인과관계가 교란받지 않을 필요충분조건은 두 확률변수가 가질 수 있는 모든 X = x, Y = y에 대해
$$P(Y = y | do(X = x)) = P(Y = y | X = x)$$
X를 랜덤하게 통제한 실험에서 관측한 두 변수간 연관성과 자연적으로 관측한 두 변수 X,Y간 연관성이 동일하다면...
두 변수 X,Y는 오직 서로만 영향을 끼치는 것이다.
3.통제를 하는 직관적인 이유
직관적인 이유는 아주 간단하다.
X를 다른 이유없이 내가 바꿨을 때 Y의 변화를 관측하는 P(Y = y|do(X = x))은 오직 X,Y의 관계를 인위적으로 관측한 것이다.
그런데 P(Y = y | X = x)인 X의 변화에 따른 Y의 변화 관계를 자연적으로 관측한 것이다.
그런데 Z가 X,Y에 모두 영향을 미치므로 X의 자연적인 변화에 Z의 영향이 반드시 있지 않겠는가
그래서 만약 P(Y = y | do(X = x)) = P(Y = y | X = x)이면 z의 영향이 없다고 보는 것이다.
4. 교란변수의 영향을 통제하는 방법
다음과 같이 가정하고
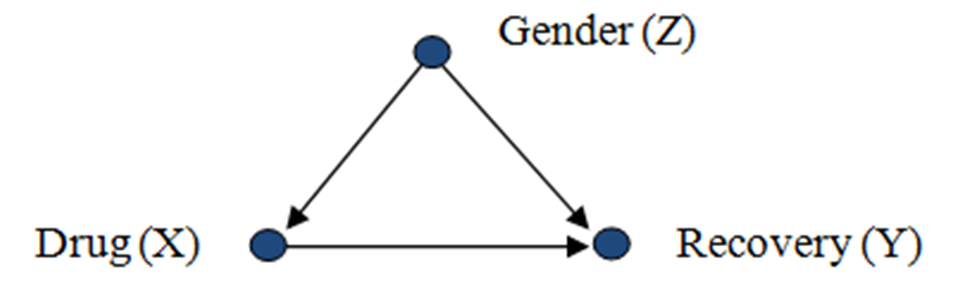
전확률법칙으로부터,

그런데 X는 Z에 영향을 미치지 않으므로,

그러므로 일반적으로 위와 같은 가정에서
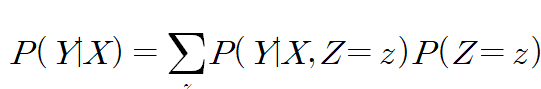
그러면 X = x로 통제한 조건부확률은...
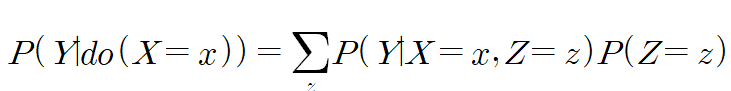
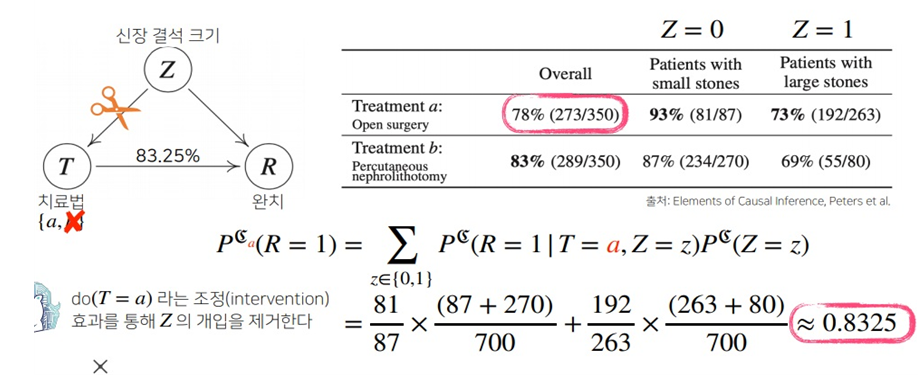
치료법 a,b에 따른 완치여부를 검사하고자 한다.
위에서 구한 식에 따르면

P(R = 1 | T = a, Z = 0)은 신장결석크기가 작은 사람한테 치료법 a를 적용할 확률 $\frac{81}{87}$이고
P(Z = 0)은 신장결석크기가 0인 사람들의 비율
전체사람은 350 + 350 = 700
Z = 0에 해당하는 사람은 87 + 270 = 357이므로 $\frac{357}{700}$
비슷하게 Z = 1에 해당하는 것도 구할 수 있다.
Z의 개입을 제거한 확률은 약 0.8325이고, 제거하지 않았을 때 조건부확률은 overall에 나온 P(R|T) = 0.78정도이다.
서로 다르기 때문에 R,T 사이에 Z의 영향이 있다고 판단할 수 있다.
'다시보는 통계학' 카테고리의 다른 글
| 왜도(skewness)에 대한 오해 - 오른쪽으로 치우친 분포와 왼쪽으로 치우친 분포? (0) | 2025.04.21 |
|---|---|
| feature scaling을 위한 정규화(normalization) 기법들 (0) | 2025.04.12 |
| 조건부확률과 베이즈정리 이론 간단하게 (0) | 2024.01.04 |
| 통계적 모델링과 최대가능도추정법(Maximum likelihood estimation) 간단하게 (0) | 2024.01.03 |
| 이상치 탐지를 위한 기본적인 isolation forest 알고리즘 (0) | 2022.09.05 |

