1. 문제
주사위를 1번 던져서 나오는 눈은 1,2,3,4,5,6이고 각각은 1/6의 확률로 나온다.
모집단의 확률변수 X=1,2,3,4,5,6을 취할 수 있고 각각이 1/6의 확률을 가지므로 평균이 3.5이고 분산은 17.5/6이 된다.
크기가 6인 모집단에서 크기 2인 표본을 단순 임의 비복원추출할 때 가능한 표본은?
(1,2), (1,3), (1,4), (1,5),...(5,6)으로 총 15개가 나온다.
이 15개의 표본에 대해 표본평균을 구하면 1.5, 2, 2.5, ...5.5가 나오고 이들의 평균이 '표본평균의 평균'으로 3.5가 나온다.
모평균과 표본평균의 평균은 동일하기 때문에 당연한 결과라고 생각할 수 있다.
표본평균의 분산은 (모분산)/n이므로 17.5/6/2 = 17.5/12가 나와야할것으로 예상되는데
표본평균 1.5, 2, 2.5, ...5.5의 분산을 구해본다면 이들의 평균이 3.5이고 편차 제곱은 4, 2.25, 1,..., 2.25,4로 나오고 이들의 합은 17.5가 나온다
분산은 '편차 제곱의 평균'이고 총 15개 존재하므로 17.5/15가 바로 표본평균의 분산이 된다.
17.5/12와 17.5/15가 서로 다르게 나오는데 왜 그럴까?
2. 표본평균의 분산
일반적으로 표본평균의 분산하면 $\sigma ^{2}/n$을 생각하지만 사실 그렇지 않다
"모집단의 크기가 N인 유한한 모집단에서 표본의 크기가 n인 표본을 simple random sampling without replacement를 수행하여 추출하면 표본평균의 분산은 $$[\frac{N-n}{N-1}]\frac{\sigma^{2}}{n}$$
그러면 모집단의 크기 N이 충분히 크다면, $\frac{N-n}{N-1}$이 1에 수렴하기 때문에 $\sigma ^{2}/n$으로 수렴하게 된다. "
그래서 $\sigma ^{2}/n$은 일반적으로 모집단의 크기는 충분히 크다고 생각하기 때문에 알려져있는 것이다.
3. 간단한 증명
모집단의 크기가 N이고 각각 개체가 $X_{1}, X_{2},..., X_{N}$이라고 하자.
여기서 표본의 크기가 n인 표본을 비복원추출로 단순임의추출하면 다음과 같은 상황이 될 것이다.

표본평균의 분산은 다음과 같이 쓸 수 있는데

$E(\bar{X}^{2})$을 먼저 계산해보면, 표본평균의 제곱 $\bar{X}_{i}^{2}$과
추출 확률 $\frac{1}{\binom{N}{n}}$의 곱의 합으로 구해진다.
비복원추출이면서 단순임의추출이라는 점을 고려할때 표본집합의 구성이 위 그림과 같이 명확하므로 수식을 다음과 같이 쓸 수 있다.

이 식을 전개하면 어떻게 될까?
예를 들어 $X_{1}^{2}$은 몇개나 있을까?
$X_{1}$을 표본집합에 먼저 포함시키고, 나머지 N-1개의 모집단 개체중에서 n-1개를 구성하면 되므로 $\binom{N-1}{n-1}$개만큼 존재한다.
나머지 $X_{2}^{2}$부터 $X_{N}^{2}$까지도 마찬가지다.

전개하면 빨간색으로 밑줄친 부분의 부가적인 항이 생기는데 저 부분은 몇개나 생길까?
실제로 모든 전개식을 더하면 아래와 같은 형태로 나올 것으로 예상된다

빨간색 ??에 들어갈 값은 어떻게 구할까? 2개의 표본 $X_{i}$와 $X_{j}$가 먼저 들어가있다고 가정하고
나머지 N-2개의 개체중에서 n-2개를 뽑는 방법의 수 $\binom{N-2}{n-2}$와 같다.
그래서 수식을 모두 전개하면 다음과 같다

여기서 $(E(\bar{X}))^2$은 어떻게 구할까?
표본평균의 평균 $E(\bar{X})$는 모집단의 평균과 동일하므로
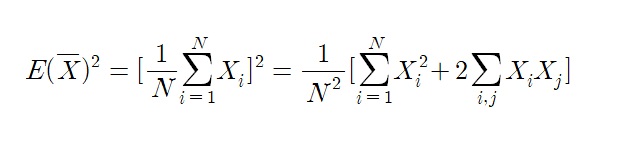
두 식의 차이가 표본평균의 분산이므로
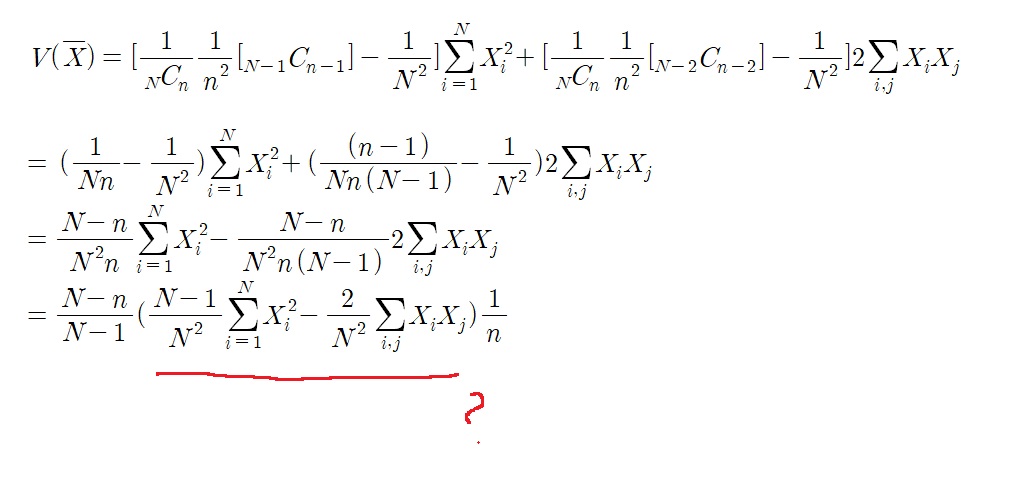
빨간색 밑줄친 부분이 문제인데... 정리해보면 모집단의 분산 $V(X)=E(X^{2})-(E(X))^{2}$임을 알 수 있다

그러므로 표본평균의 분산은 다음과 같다.

'다시보는 통계학' 카테고리의 다른 글
| 이상치 탐지를 위한 기본적인 isolation forest 알고리즘 (0) | 2022.09.05 |
|---|---|
| Wilcoxon rank sum test(Mann–Whitney U test)는 등분산성을 가정하고 있다 (0) | 2022.06.11 |
| 추정량의 오차는 왜 추정량의 표준편차일까? (0) | 2022.06.01 |
| 피어슨 상관계수, 스피어만 상관계수, 켄달의 타우 완벽비교 (0) | 2022.05.23 |
| 재현율(recall)에 대해 정확히 알기 (0) | 2022.04.07 |

