1. 비지도학습을 이용한 이상치 탐지(anomaly detection)
1-1) mahalanobis 거리를 이용한 outlier 탐지
1-2) k-means를 이용한 군집화
1-3) DBSCAN
1-4) isolation forest
2. isolation forest
isolation을 이용하여 이상치를 탐지하는 알고리즘이다.
isolation은 데이터의 나머지보다 특정 데이터 포인트가 얼마나 멀리 떨어져있는지를 나타내는 것이다.
기본적으로 이상치는 다른 정상데이터보다 분리시키기 쉽다는 성질을 이용한다

decision tree의 재귀 이진 분할을 활용하여 랜덤하게 변수를 선택하고, 이를 이용해 모든 데이터를 재귀 이진분할 시킨다.
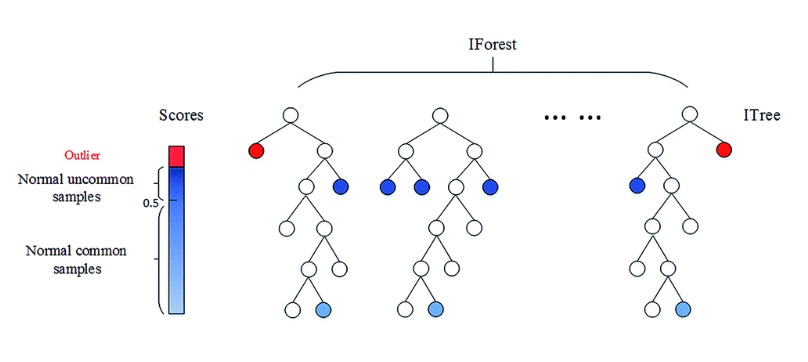
이상치가 분할하기 쉬우므로 상대적으로 root node에 가까운 곳에 분리되어있고
정상 데이터는 더 많은 분할을 해야하므로 leaf node에 가까운 곳에 분리되어 있다
------------------------
3. 알고리즘
decision tree처럼 iTree라는 것을 앙상블하여 forest를 만드는 방식
3-1) 비복원 추출로 데이터중 일부를 sampling하고
3-2) 데이터 X의 변수 중에서 q를 랜덤하게 선택함
3-3) 변수 q의 min~max중에서 uniform 분포에 의해 split point를 선택
3-4) 모든 관측치가 split되거나, 지정한 임의의 split 횟수까지 반복하여 경로의 길이를 저장함
3-5) 위 과정을 여러번 반복한 tree를 여러개 만들어 앙상블
4. 데이터의 이상지수 score
랜덤하게 변수를 선택하여 분할하기 때문에 여러개의 isolation tree의 앙상블로 데이터의 이상지수 score를 산정함
0~1사이의 값을 가지며 tree의 수는 50~100개정도면 score가 안정적이라는 논문 결과가 있다
데이터 x가 분할된 tree 경로의 길이가 h(x)이고 이것의 기댓값 E(h(x))는 앙상블한 모든 tree에 대한 데이터 x의 평균 관측 경로
c(n)은 h(x)를 normalize하기 위한 iTree의 평균 경로 길이라고 함

그럴때, x의 이상지수 s(x,n)은
$$s(x,n) = 2^{\frac{-E(h(x))}{c(n)}}$$

관측치 x가 이상치라면, 경로 길이가 평균적으로 0에 가까워서 E(h(x))가 0에 가까워지므로, s(x,n)은 1에 가까워지고
관측치 x가 전체 경로길이의 평균과 비슷하여 정상데이터라면, E(h(x))가 c(n)과 비슷하여, s(x,n)은 0.5와 가까워진다
관측치 x가 최대경로길이를 가진다면 E(h(x))가 n-1에 가까워져서 s(x,n)은 0에 가까워진다
그래서 score는 1에 가까울수록 이상치로 판단하고
0.5이하일수록 정상데이터로 판단한다고 한다.
모든 데이터의 score가 0.5에 가깝다면 이상치를 발견하지 못한것으로 판단할 수 있다
5. 특징
5-1)전체 데이터가 아닌 sampling한 데이터로 모델링(군집화는 전체 데이터를 사용함)
5-2)이상치가 정상데이터와 가까이 위치하면, 당연히 이상치도 분할수가 많아지므로 분류하기 어려울 수 있다.
그래서 데이터의 random sampling으로 이러한 효과를 줄이고자 한다고 함. 특히 sampling point를 줄이면 이런 효과를 방지할 수 있는 하나의 해결책이 될 수 있음
5-3) 비슷하게 이상치가 서로 군집화되어 있는 경우도 잘못 분류할 가능성이 높은데 sampling을 통해 이러한 효과를 방지한다
5-4) training 데이터에 이상치가 없더라도 isolation forest의 성능에는 아무 상관이 없다.
score 산정 방식을 보면 납득할 수 있음.. 없으면 score가 전부 0.5일테니까 없다고 판정하니까
5-5) 너무 고차원의 데이터에는 거리 기반의 분할을 이용한 isolation forest가 잘 작동하지 않을 수 있다.
차원이 높아질수록 sparse한 차원이 많아져서 거리 계산에 비효율적이라 split을 잘 못함
차원을 줄이는 여러 방법을 사용하여 성능을 대폭 개선할 수는 있다?
6. 코드
sklearn에서 모델을 제공함
https://dodonam.tistory.com/129
Isolation Forest (for anomaly detection)
Isolation Forest - Tree를 이용한 이상탐지를 위한 비지도학습 알고리즘 - Regression Decision Tree를 기반으로 실행 - Regression Tree 가 재귀 이진 분할을 이용하여 영역을 나누는 개념을 이용함 Random fore..
dodonam.tistory.com
https://velog.io/@vvakki_/Isolation-Forest-%EB%AF%B8%EC%99%84%EC%84%B1
Isolation Forest
[Post No.002] Isolation Forest 개념
velog.io
https://en.wikipedia.org/wiki/Isolation_forest#Algorithm
Isolation forest - Wikipedia
From Wikipedia, the free encyclopedia Jump to navigation Jump to search Algorithm for anomaly detection Isolation forest is an anomaly detection algorithm. It detects anomalies using isolation (how far a data point is to the rest of the data), rather than
en.wikipedia.org
'다시보는 통계학' 카테고리의 다른 글
| 조건부확률과 베이즈정리 이론 간단하게 (0) | 2024.01.04 |
|---|---|
| 통계적 모델링과 최대가능도추정법(Maximum likelihood estimation) 간단하게 (0) | 2024.01.03 |
| Wilcoxon rank sum test(Mann–Whitney U test)는 등분산성을 가정하고 있다 (0) | 2022.06.11 |
| 표본평균의 분산은 $\sigma ^{2}/n$이 아니다 (0) | 2022.06.09 |
| 추정량의 오차는 왜 추정량의 표준편차일까? (0) | 2022.06.01 |

