1. 조건부확률
P(A|B)는 사건 B가 일어난 상황에서 사건 A가 발생할 확률
P(A∩B)=P(B)P(A|B)
2. 조건부확률 시각화
민감도, 특이도, 정밀도,재현율, F1score를 구분함

그림의 정밀도가 정확도

귀무가설 H0 :음성, 대립가설 H1 :양성
실제로 걸리진 않았는데(귀무가설이 참) 걸렸다고 검진(귀무가설 기각)한 경우 False positive는 1종오류
실제로 걸렸는데(대립가설이 참) 검진하지 못한(대립가설 기각) 경우 False Negative는 2종오류
보통 정확도는 False Positive가 커질 경우 떨어진다(식만 봐도 알 수 있음)
보통 1종오류보다 2종오류가 심각하여, 1종오류를 조금 희생하더라도 2종오류를 줄이려고 한다
위에 1종,2종오류 의미만 보더라도 실제로 걸렸는데, 안걸렸다고 하는 2종오류가 심각하다는건 명확함
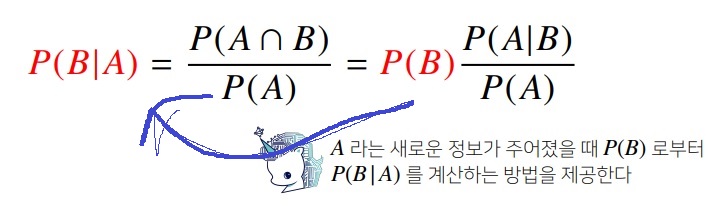
3. 베이즈정리
베이즈 정리는 조건부확률을 이용해 정보를 갱신하는 방법을 알려준다

사전확률은 모델링하기 전 모수의 확률분포
사후확률은 데이터를 관찰하고 나서의 갱신된 모수의 확률분포
Evidence는 데이터의 확률분포
가능도는 고정된 모수에서 관찰된 데이터를 뽑을 가능성
베이즈 정리는 데이터를 관측할 때마다 확률모형을 계속 갱신해나간다는 점에서 의미있다.

728x90
'다시보는 통계학' 카테고리의 다른 글
| feature scaling을 위한 정규화(normalization) 기법들 (0) | 2025.04.12 |
|---|---|
| 상관관계는 인과관계가 아니다 - confounder model(교란변수 모델) (0) | 2024.04.20 |
| 통계적 모델링과 최대가능도추정법(Maximum likelihood estimation) 간단하게 (0) | 2024.01.03 |
| 이상치 탐지를 위한 기본적인 isolation forest 알고리즘 (0) | 2022.09.05 |
| Wilcoxon rank sum test(Mann–Whitney U test)는 등분산성을 가정하고 있다 (0) | 2022.06.11 |

