1. 상관계수(correlation coefficient)
두 변수의 통계적 관계를 나타내는 상관관계의 정도를 수치로 나타낸 값
-1부터 1까지의 값을 가지며, 0인 경우는 상관관계가 없다고 말한다.
세가지 성질을 가지는 것이 좋다.
1)두 변수의 값이 완전한 부합이면 +1, 완전한 비부합이면 -1
2)두 변수가 서로 독립이면 0
3)두 변수에 대해 크기의 순서가 보존되는 변환을 수행해도 상관계수의 값은 변하지 않는다
수치를 확인하기 전에 산점도(scatter plot)를 먼저 그리고 수치적으로 파악하는 것이 기본
2. 피어슨 상관계수(pearson)
두 변수 X,Y의 선형적 관계(linear relationship)의 측도
선형적 관계가 강하다는 것은 선형모형에 의해 두 변수의 관계를 잘 모델링할 수 있다는 의미
오직 선형적 관계만을 반영하며 다른 (비선형적) 관계는 무시한다
1에 가까울수록 양의 선형관계, -1에 가까울수록 음의 선형관계, 0에 가까울수록 선형관계가 없다
1과 -1이면 모든 데이터가 완전히 직선위에 놓인다는 뜻이다.
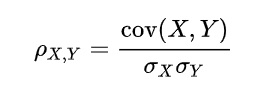

'3)두 변수에 대해 크기의 순서가 보존되는 변환을 수행해도 상관계수의 값은 변하지 않는다'를 만족하지 않는다.
순서를 보존하는 어떤 변환에서 피어슨 상관계수 값이 변할 수 있다고 한다
3. 피어슨 상관계수에 대한 검정
두 변수의 독립성 검정을 위해 '피어슨 상관계수가 0이다'를 검정할 수 있다
피어슨 상관계수가 0이라는 것은 두 변수가 통계적으로 독립이라는 뜻
H0: 피어슨 상관계수는 0이다.
H1: 피어슨 상관계수는 0이 아니다
검정통계량 $T=r\frac{\sqrt{n-2}}{\sqrt{1-r^{2}}}$가 귀무가설이 참일 때 t(n-2)를 따른다.
따라서 피어슨 상관계수에 대한 검정은 분포를 가정하는 모수적검정이다.
4. 스피어만 순위상관계수(spearman)
두 변수의 순위(rank)에 대한 피어슨 상관계수와 정확히 동일하다.
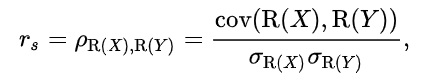
특별한 조건하에서 다음과 같은 식으로 변형될 수 있다.

스피어만 상관계수는 두 변수 사이의 단조성(monotonic relationship)을 측정한다.
바로 위 그림에서 $d_{i}$가 작을수록 스피어만 순위상관계수는 커진다.
$d_{i}$는 두 순위의 차이를 나타내는 것으로 순위 차이가 작다는 것은
X가 커지면 Y도 커지는 경향을 보이고, X가 작아지면 Y도 작아지는 경향을 보인다는 뜻이다.
1에 가까울수록 강한 양의 단조관계를 보이고, -1에 가까울수록 강한 음의 단조관계를 보인다.
0에 가까울수록 단조관계가 거의 없다는 뜻이다.
스피어만 상관계수는 순서형 변수에 적절하다.(약간 애매한데??)
피어슨 상관계수와는 달리 3번째 성질 '순서보존 변환에도 불변'을 만족?
5. 선형관계(linear relationship)와 단조관계(monotonic relationship)
선형관계는 두 변수의 데이터가 직선에 의해 모델링될 수 있다는 의미
단조관계는 쉽게말하면 단조관계 = 비선형관계, 선형관계를 모두 포함하는 개념
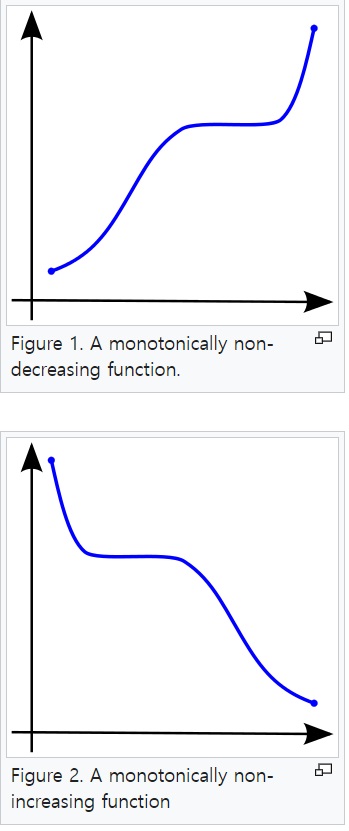
수학적으로 단조적 증가(monotonic increasing)는
모든 X,Y의 값에 대하여 서로 대응하는 X1<>Y1, X2<>Y2가 X1 <= X2이면 Y1 <= Y2을 만족하는 것
>>> X가 증가하면 Y도 증가하는 경향
단조적 감소(monotonic decreasing)은 X1 <= X2이면 Y1 >= Y2인 것이다.
>>> X가 증가하면 Y는 감소하는 경향

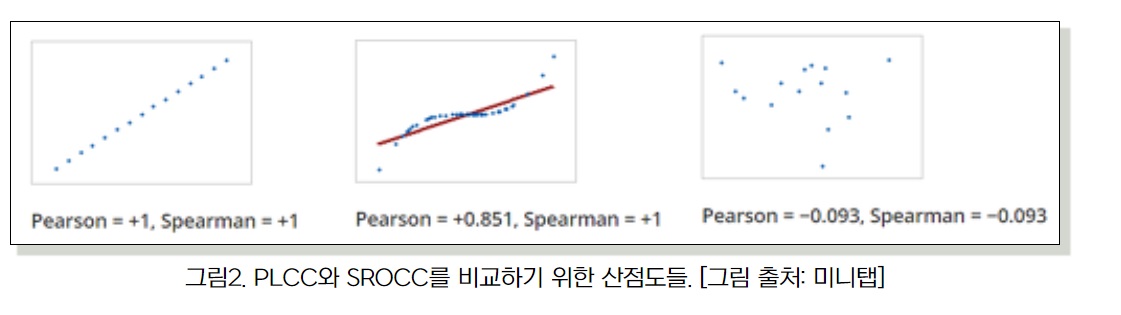
2번째 그림을 보면 알수있지만 단조관계를 나타내는 그림으로, 스피어만 상관계수는 1이지만 선형관계를 반영하는 피어슨 상관계수는 1보다 작다는 것을 알 수 있다.
그래서 그림을 그려보고 수치를 구하는 것이 중요하다.
6. 스피어만 순위상관계수 검정
두 변수가 독립인지 검정하기 위해 '스피어만 순위상관계수가 0이다'를 검정할 수 있다.
스피어만 상관계수가 0이다라는 것은 두 변수가 통계적으로 서로 독립이라는 뜻
두 변수 순위 차이 $d_{i}$를 이용한 분포무관 비모수적 검정이다.

순위 동점이 존재하지 않는 경우 검정통계량은 위와 같다. $d_{i}$는 $X_{I}$와 $Y_{i}$의 순위 차이
귀무가설 H0: 스피어만 상관계수는 0
대립가설 H1: 스피어만 상관계수는 0이 아니다.
귀무가설이 참일 때 검정통계량의 기댓값이 0이고 분산이 $\frac{1}{n-1}$이다.
표본이 충분히 크면 $z = \frac{r-E(r)}{\sqrt{Var(r)}} = \sqrt(n-1)r$이 N(0,1)을 근사적으로 따른다.
동점이 존재하면 동점끼리의 평균순위를 사용하고 위 공식 대표본근사 공식을 사용한다고함
r이 충분히 크면 H1:스피어만 상관계수>0를 채택
r이 충분히 작으면 H1:스피어만 상관계수<0를 채택
r이 충분히 크거나 충분히 작으면 H1:스피어만 상관계수가 0이 아니다를 채택
7. 켄달의 타우
스피어만 순위상관계수와 동일하게 두 변수 사이의 단조적 관계(monotonic relationship)를 측정한다
특히 스피어만 상관계수와 켄달의 타우는 rank correlation(ordinal association)을 측정한다고 말한다.
두 변수의 rank에 대한 관계를 측정한다
1에 가까울수록 강한 양의 순서적 관계(rank correlation)로 X가 커지면 Y도 커지는 경향이 강하다는 뜻
-1에 가까울수록 강한 음의 순서적 관계(rank correlation)으로 X가 커지면 Y는 작아지는 경향이 강하다
0에 가까울수록 순서적 관계가 거의 없다는 뜻
스피어만 상관계수처럼 3번 성질, '순서보존 변환에 대한 불변'을 만족?

concordant라는 것은 $i<j$에서 $(X_{i},X_{j})$, $(Y_{i},Y_{j})$에 대하여 $X_{i} < X_{j}, Y_{i} < Y_{j}$를 만족시키거나
$X_{i} > X_{j}, Y_{i} > Y_{j}$를 만족시킨다는 뜻이다.
concordant인 수가 많을수록 켄달의 타우가 1에 가까워질 것이고, 그것은 x가 증가하면 y도 증가하는 경향이 있다는 뜻
즉 $(X_{i}-X_{j})(Y_{i}-Y_{j})>0$인 데이터 쌍 $(X_{i},Y_{i})$, $(X_{j},Y_{j})$의 수
반대로 discordant라는 것은 $(X_{i}-X_{j})(Y_{i}-Y_{j})<0$인 데이터 쌍 $(X_{i},Y_{i})$, $(X_{j},Y_{j})$의 수
8. 켄달의 타우에 대한 검정
두 변수가 서로 독립인지 검정하기 위해 귀무가설 H0: '켄달의 타우가 0이다'를 검정
켄달의 타우가 0이다라는 것은 두 변수가 통계적으로 서로 독립이라는 뜻
분포를 가정하지 않는 분포무관 비모수적 검정
concordant인 수 즉, $(X_{i}-X_{j})(Y_{i}-Y_{j})>0$인 데이터 쌍 $(X_{i},Y_{i})$, $(X_{j},Y_{j})$의 수가 P이고
discordant인 수 즉, $(X_{i}-X_{j})(Y_{i}-Y_{j})<0$인 데이터 쌍 $(X_{i},Y_{i})$, $(X_{j},Y_{j})$의 수가 Q이면
K=P-Q를 검정통계량으로 사용
K가 충분히 크면 H1:켄달의 타우>0를 채택
K가 충분히 작으면 H1:켄달의 타우<0를 채택
K가 충분히 크거나 충분히 작으면 H1:켄달의 타우가 0이 아니다를 채택
9. 어떤 상관계수??
순서형변수에만 스피어만 상관계수 사용해야지~ 이런 느낌보다는
주어진 변수가 어떤 변수인지,
선형적관계를 봐야할지, 단조적 관계,비선형적 관계를 봐야할지, 종합적으로 고려해서 사용해야할듯?
참고
Pearson 상관계수, Spearman 상관계수, Kendall 상관계수란?
두 변수 간의 상관성을 평가하기 위해, 또는 ground-truth 라벨들과 알고리즘을 통해 예측된 라벨들을 비교하기 위해 일반적으로 Pearson 상관계수, Spearman 상관계수, Kendall 상관계수를 계산합니다. 이
bskyvision.com
https://en.wikipedia.org/wiki/Pearson_correlation_coefficient
Pearson correlation coefficient - Wikipedia
From Wikipedia, the free encyclopedia Jump to navigation Jump to search Measure of linear correlation In statistics, the Pearson correlation coefficient (PCC, pronounced ) ― also known as Pearson's r, the Pearson product-moment correlation coefficient (P
en.wikipedia.org
'다시보는 통계학' 카테고리의 다른 글
| 표본평균의 분산은 $\sigma ^{2}/n$이 아니다 (0) | 2022.06.09 |
|---|---|
| 추정량의 오차는 왜 추정량의 표준편차일까? (0) | 2022.06.01 |
| 재현율(recall)에 대해 정확히 알기 (0) | 2022.04.07 |
| 표집분포(sampling distribution)와 표본분포(sample distribution) (0) | 2022.02.21 |
| 조건부독립의 성질 (0) | 2022.01.30 |

