1. 몬티 홀 문제(monty hall problem)
극한탈출 시간의 딜레마(zero escape time dilemma) 플레이 중 흥미로운 문제가 등장했다.
갇혀진 밀실에 이산화탄소가 쏟아져 나오고 있다.
이 이산화탄소는 20분동안 나오는데, 산소마스크를 쓰지 않는다면 죽게될 위기에 처했다.
이제 10개의 로커함이 주어진다
이 로커함중 단 한 곳에만 산소마스크가 있다.
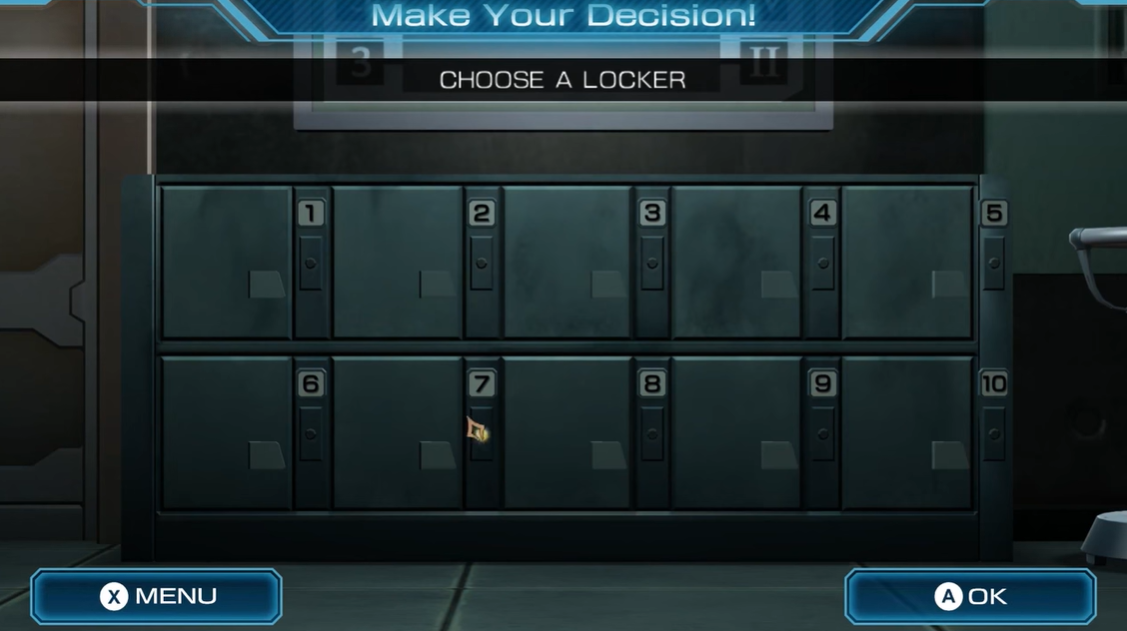
정확히 한 곳만 골라 열어볼 수 있다고 할때, 산소마스크가 당첨될 확률은?
당연히 $\frac{1}{10}$이다.
어느 한 곳을 선택했는데, 이제 사회자가 다음과 같은 제안을 한다.
"나는 산소마스크가 어디에 있는지 알고 있다.
당신이 선택한 곳에 산소마스크가 존재한다면, 나는 나머지 9개의 문 중 8개의 문을 랜덤하게 열어줄 것이다.
하지만 당신이 선택한 곳에 산소마스크가 존재하지 않는다면, 나는 나머지 9개의 문 중 상품이 없는 8개의 문을 열어줄 것이다."
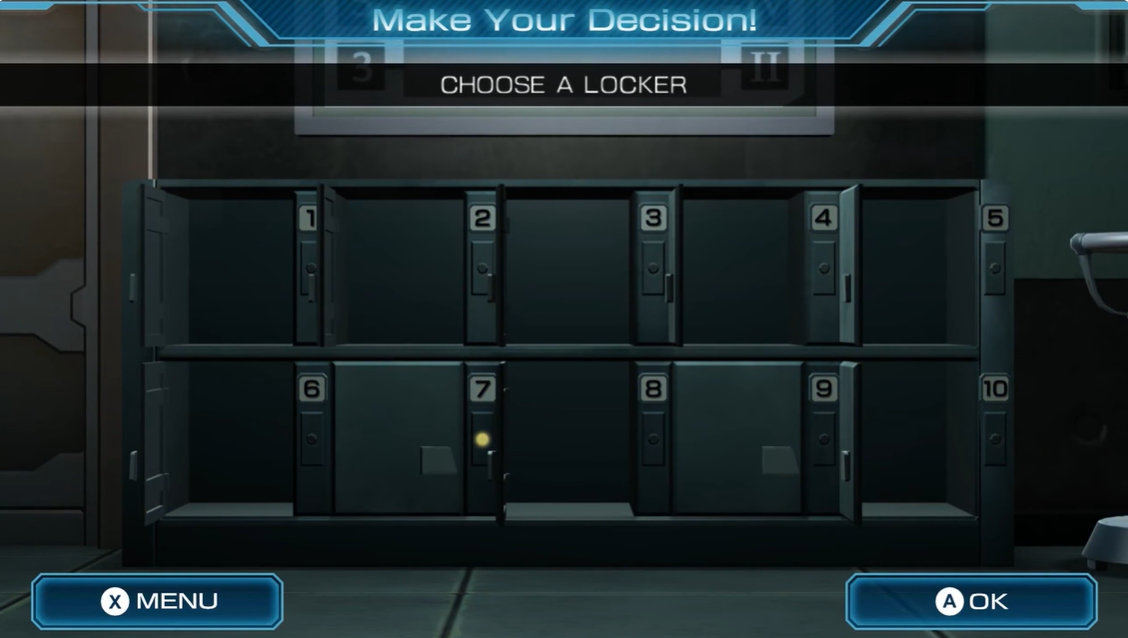
이제 사회자가 선택을 바꿀 기회를 준다.
나는 선택을 바꾸는 것이 유리한가? 바꾸지 않는 것이 유리한가?
2. 가장 쉬운 문제
문의 개수 n = 3인 경우가 가장 간단한 형태의 문제이고 잘 알려진 문제이다.
게임 쇼에 참가하여 세 개의 문 중 하나를 고른다고 가정해 봅시다. 하나의 문 뒤에는 차가 있고, 다른 두 개의 문 뒤에는 염소가 있습니다. 예를 들어 문 1을 선택했다고 가정하고, 사회자는 문 뒤에 무엇이 있는지 알고 있습니다. 그리고 문 3을 열어 염소가 있다는 것을 보여줍니다. 그런 다음 사회자는 "문 2로 바꾸겠습니까?"라고 묻습니다. 문을 바꾸는 것이 유리할까요?
각 문에 존재할 수 있는 경우를 생각해보면
| 문 1 | 문 2 | 문 3 |
| 염소 | 염소 | 차 |
| 염소 | 차 | 염소 |
| 차 | 염소 | 염소 |
이제 1번 문을 선택했다고 생각해보자.
사회자는 항상 염소가 있는 문을 열어주므로, 첫번째 경우에
문1 : 염소
문3 : 차
2가지 경우가 남아있다.
이때, 선택을 바꾸면 차를 얻지만, 선택을 바꾸지 않으면 염소를 얻는다.
두번째 경우도 마찬가지다.
문1: 염소
문2: 차
선택을 바꾸면 차를 얻지만, 선택을 바꾸지 않으면 염소를 얻는다.
세번째 경우는
문1: 차
문2나 문3중 하나가 랜덤하게 닫혀있다. : 염소
선택을 바꾸면 염소를 얻지만, 선택을 바꾸지 않으면 차를 얻는다.
따라서 가능한 3가지 경우중 선택을 바꾸면 2가지가 차를 얻고 1가지가 염소를 얻기 때문에, 선택을 바꾸면 $\frac{2}{3}$의 확률로 차를 얻는다.
반대로 선택을 바꾸지 않으면 2가지가 염소를 얻고 1가지가 차를 얻으므로 선택을 바꾸지 않으면 $\frac{1}{3}$의 확률로 차를 얻는다.
3. 전제 조건
1) 사회자는 참가자가 선택하지 않은 문을 항상 열어야 한다.
2) 사회자는 항상 염소가 있는 문을 열어야하고, 절대로 차가 있는 문을 열지 않는다.
3) 사회자는 항상 참가자가 처음 선택한 문과, 남아있는 닫힌 문 사이에서 바꿀 기회를 제공한다.
4. 오해
대부분의 사람들은 두 개의 닫힌 문 중 하나에 차가 있을 확률이 50%라고 생각하여 바꾸는 것이 중요하지 않다고 결론짓습니다.
이는 사회자가 무작위로 문을 열었다면 사실일 수 있지만, 실제로는 그렇지 않습니다.
사회자가 여는 문은 참가자의 초기 선택에 따라 달라지므로, 선택 간의 독립성 가정이 성립하지 않습니다.
사회자가 문을 열기 전에는 각 문 뒤에 차가 있을 확률이 각각 1/3입니다.
만약 차가 1번 문 뒤에 있다면, 사회자는 2번이나 3번 문 중 아무 문이나 열 수 있으므로, 차가 1번 문 뒤에 있고 사회자가 3번 문을 여는 확률은 1/3 × 1/2 = 1/6입니다.
반면, 차가 2번 문 뒤에 있고 참가자가 1번 문을 선택한 경우, 사회자는 반드시 3번 문을 열어야 하므로 이 확률은 1/3 × 1 = 1/3입니다.
사회자가 3번 문을 여는 경우는 이 두 가지밖에 없으므로, 참가자가 1번 문을 선택하고 사회자가 3번 문을 열었다면, 차가 2번 문 뒤에 있을 확률은 1번 문보다 두 배 더 높습니다.
핵심은 차가 2번 문에 있을 경우 사회자는 반드시 3번 문을 열어야 하지만, 차가 1번 문에 있을 경우 사회자는 2번이나 3번 중 하나를 선택할 수 있다는 점입니다.
5. 직관적인 해법
해결책을 이해하는 또 다른 방법은, 참가자가 처음에 선택하지 않은 두 개의 문을 하나의 세트로 묶어 생각하는 것입니다.
‘당신은 당신이 선택한 하나의 문을 그대로 유지할 수도 있고, 나머지 두 개의 문을 선택할 수도 있습니다.’”
사회자는 차가 어디 있는지 알고 있기 때문에 반드시 염소가 있는 문을 열며, 이로 인해 두 개의 문 중 하나가 열렸다고 해서 차가 있을 확률 2/3는 변하지 않습니다.
즉, 사회자가 문 하나를 연 후 참가자에게 선택을 바꿀 기회를 제공하는 것은, 처음 선택한 한 개의 문을 유지할지 아니면 나머지 두 개 문 전체(단, 이 중 하나는 이미 열려 있음)를 선택할지를 제안하는 것과 본질적으로 동일합니다.
이 경우, 선택을 바꾸는 전략은 여전히 참가자가 차를 얻을 확률 2/3를 제공하므로, 바꾸는 것이 유리합니다.
6. 조건부 확률
"사회자는 내가 고른 문을 열지 않는다",
"사회자는 자동차와 염소가 어떤 문에 있는지 알고 있다"는 전제조건과,
이에 따라 "사회자가 자동차가 있는 문을 여는 일은 절대 발생하지 않는다"는 종속조건이 실제 확률에 영향을 미치기 때문이다.
이 문제에서 사회자가 염소 문을 하나 열었을 때 선택한 문을 바꾸는 행위는 염소 확률과 자동차 확률을 뒤바꾸게 된다.
결정을 바꾼다는 전제하에 2/3 확률로 염소를 고르면 차를 얻으니까 처음 염소를 뽑을 확률이 높으니 무조건 바꿔야한다!
결정을 바꾸지 않는다면 당신은 맨 처음 차를 뽑았을 확률인 1/3을 그대로 들고 가는 것이기 때문에 더 손해를 보게 된다.
몬티 홀 딜레마에서 가장 중요한 개념은 결과를 바꾸는 선택이 어느 문을 고르냐가 아니라 문을 바꾸느냐 안 바꾸느냐라는 것이다.
애초에 처음부터 하나의 문이 열려 있고 나머지 둘 중 하나를 선택해야 하는 것이라면, 열린 문은 애초에 선택지로 고려하지 않으므로 확률은 50%가 맞다.
즉 양자택일의 행위가 아닌, 문을 바꾸는 행위에서 파생되는 확률이 66.6%이므로 둘은 엄연히 다르다.
이 미묘한 차이를 직관적으로 이해하기가 힘들기 때문에 착오가 벌어지는 것이라고 이해해야 한다.
문을 바꾸거나 바꾸지 않거나 2가지 중 하나이므로,
1) 나는 문을 바꾼다
1-1) 처음에 염소가 있는 문을 선택할 확률은 2/3
- 사회자는 무조건 염소가 있는 문을 선택하므로 확률은 1/1
- 문을 바꿀 경우 자동차가 있을 확률은 1/1
- 2/3 * 1/1 * 1/1 = 2/3
1-2) 처음에 자동차가 있는 문을 선택할 확률은 1/3
- 사회자가 염소가 있는 문 중 첫번째 것을 선택할 확률은 1/2
- 문을 바꿀 경우 자동차가 있을 확률은 0/1
- 1/3 * 1/2 * 0/1 = 0
- 사회자가 염소가 있는 문 중 두번째 것을 선택할 확률은 1/2
- 문을 바꿀 경우 자동차가 있을 확률은 0/1
- 1/3 * 1/2 * 0/1 = 0
따라서 전체 확률은 2/3
2) 나는 문을 바꾸지 않는다.
1-1) 처음에 염소가 있는 문을 선택할 확률은 2/3
- 사회자는 무조건 염소가 있는 문을 선택하므로 확률은 1/1
- 문을 바꾸지 않을 경우 자동차가 있을 확률은 0/1
- 2/3 * 1/1 * 0/1 = 0
1-2) 처음에 자동차가 있는 문을 선택할 확률은 1/3
- 사회자가 염소가 있는 문 중 첫번째 것을 선택할 확률은 1/2
- 문을 바꾸지 않을 경우 자동차가 있을 확률은 1/1
- 1/3 * 1/2 * 1/1 = 1/6
- 사회자가 염소가 있는 문 중 두번째 것을 선택할 확률은 1/2
- 문을 바꾸지 않을 경우 자동차가 있을 확률은 1/1
- 1/3 * 1/2 * 1/1 = 1/6
따라서 전체 확률은 0 + 1/6 + 1/6 = 1/3
7. 베이지안 관점
베이지안 관점에 의하면 아무런 정보가 없을때 a문, c문에 자동차가 있을 확률은 P(A) = P(C) = 1/3이지만,
사회자가 b문을 열어주었다는 정보가 있다면 P(C|Db) = 2/3으로 2배가 늘었다.
그만큼 c문에 차가 있을 확신이 정보에 의해 늘었다는 것이다.
8. 파이썬 시뮬레이션
import random
r = 100000
no_change_win = 0
no_change_lose = 0
change_win = 0
change_lose = 0
n = 3
door = list(range(1,n+1))
for _ in range(r):
answer = random.choice(door) #정답
choose = random.choice(door) #선택
#실제 정답과 참가자가 선택한 문을 제외한 나머지 문 중 하나
#즉, 열어줘야할 문
temp = random.choice(door)
while (answer == temp) or (choose == temp):
temp = random.choice(door)
#바꾸지 않은 경우
if answer == choose:
no_change_win += 1
else:
no_change_lose += 1
#바꾼 경우
change = random.choice(door)
#참가자는 이전에 선택한 choose, 사회자가 연 문 temp을 제외한 나머지 중 하나를 선택
while (change == choose) or (change == temp):
change = random.choice(door)
if answer == change:
change_win += 1
else:
change_lose += 1
#문을 바꾸지 않아서 이길 확률
print('바꾸지 않으면: ',no_change_win/(no_change_win + no_change_lose))
#문을 바꿔서 이길 확률
print('바꾸면: ', change_win/(change_win + change_lose))

9. 문이 n개인 경우
일반적으로 문이 n개인 경우는 어떨까?
이 경우 가능한 것은 다음과 같다.
n개의 문이 있는데, 사회자가 선택한 문을 제외한 나머지 n-1개의 문 중에서 p개의 문을 랜덤하게 열어주는 경우
참가자가 문을 바꿔서 차를 얻는 사건을 X라 하면, 구하고자 하는 확률은 P(X)이다.
참가자는 2가지 경우가 있다.
처음에 차를 고르거나, 처음에 염소를 고르거나
처음에 차를 고르는 사건을 A, 염소를 고르는 사건 B라고 하자.
P(A) = 1/N, P(B) = (N-1)/N
전확률 법칙에 의하면, 문을 바꿔서 차를 얻는 사건 X는
"처음에 차를 고르고, 문을 바꿔서 차를 얻는 사건 $X \cap A$, 처음에 염소를 고르고 문을 바꿔서 차를 얻는 사건 $X \cap B$"
2가지로 분할 되므로,
$$P(X) = P(X \cap A) + P(X \cap B) = P(X|A)P(A) + P(X|B)P(B)$$
처음에 차를 고른 경우 문을 바꿔서 차를 얻을 수 없으므로, P(X|A) = 0
처음에 염소를 고른 경우 나머지 N-1개의 문 중 차가 있는 문은 1개, N-2개의 문은 염소가 있는데 이 염소가 있는 문 중
p개의 문이 열리게 된다.
따라서 차가 있는 문 1개 + 염소가 있는 문 N-p-2개 = N-p-1개의 문이 고르지 않은 문 중에 닫혀있고,
내가 선택한 문을 바꾼다면 이 중 1개의 문에 차가 있으므로 P(X|B) = 1/(N-p-1)
따라서, $$P(X) = 0 + 1/(N-p-1) * (N-1)/N = N-1 / (N*(N-p-1))$$
이 확률은 항상 1/N보다 크다.
따라서 바꾸는 것이 유리하다. 이는 N이 크면 클수록 1에 수렴하기 때문에 더욱 명백해진다.
--------------------------------------------------------------------------------------------------------------------------------------------------------
"나는 산소마스크가 어디에 있는지 알고 있다.
당신이 선택한 곳에 산소마스크가 존재한다면, 나는 나머지 9개의 문 중 8개의 문을 랜덤하게 열어줄 것이다.
하지만 당신이 선택한 곳에 산소마스크가 존재하지 않는다면, 나는 나머지 9개의 문 중 상품이 없는 8개의 문을 열어줄 것이다."
첫번째 제시한 문제는 n = 10이고 p = 8인 문제이다.
10개의 문이 있고, 선택하지 않은 9개 중 8개를 열어준다.
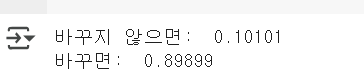
그러므로 내가 문을 바꿔서 이길 확률은 9/(10*(10-9)) = 9/10이다.
따라서, 문을 바꾸는 것이 압도적으로 유리하다.
import random
r = 100000
no_change_win = 0
no_change_lose = 0
change_win = 0
change_lose = 0
n = 10
p = 8
door = list(range(1,n+1))
for _ in range(r):
answer = random.choice(door) #정답
choose = random.choice(door) #선택
#실제 정답과 참가자가 선택한 문을 제외한 나머지 문 중 p개의 문
#즉, 열어줘야할 문
temp = []
while len(temp) < p:
c = random.choice(door)
if answer != c and choose != c:
if c not in temp:
temp.append(c)
#바꾸지 않은 경우
if answer == choose:
no_change_win += 1
else:
no_change_lose += 1
#바꾼 경우
change = random.choice(door)
#참가자는 이전에 선택한 choose, 사회자가 연 문 temp을 제외한 나머지 중 하나를 선택
while (change == choose) or (change in temp):
change = random.choice(door)
if answer == change:
change_win += 1
else:
change_lose += 1
#문을 바꾸지 않아서 이길 확률
print('바꾸지 않으면: ',no_change_win/(no_change_win + no_change_lose))
#문을 바꿔서 이길 확률
print('바꾸면: ', change_win/(change_win + change_lose))
10. 변형된 몬티 홀 문제
사회자의 행동에 따라 정답이 달라질 수 있다.
고전적인 문제는 사회자의 행동이 다음과 같음을 가정하고 있다.
1) 사회자는 참가자가 선택하지 않은 문을 항상 열어야 한다.
2) 사회자는 항상 염소가 있는 문을 열어야하고, 절대로 차가 있는 문을 열지 않는다.
3) 사회자는 항상 참가자가 처음 선택한 문과, 남아있는 닫힌 문 사이에서 바꿀 기회를 제공한다.
https://en.wikipedia.org/wiki/Monty_Hall_problem
Monty Hall problem - Wikipedia
From Wikipedia, the free encyclopedia Probability puzzle In search of a new car, the player chooses a door, say 1. The game host then opens one of the other doors, say 3, to reveal a goat and offers to let the player switch from door 1 to door 2. The Monty
en.wikipedia.org
1) 사회자가 항상 염소가 있는 문을 열고, 항상 바꿀 기회를 제공함
단, 두 염소 중 선택할 수 있는 경우에는 왼쪽 염소를 선택할 확률이 p, 오른쪽 문을 선택할 확률이 q = 1 − p.
즉 염소가 있는 문 중, 어떤 문을 열어줄지 그 확률이 동일하지 않다.
→ 사회자가 오른쪽 문을 열었을 경우 (확률 P = 1/3 + q/3), 바꾸면 이길 확률은 1 / (1 + q)
→ 왼쪽 문을 열었을 경우, 바꾸면 이길 확률은 1 / (1 + p)
→ 항상 바꾸는 전략의 전체 성공 확률:
(1/3 + q/3)/(1 + q) + (1/3 + p/3)/(1 + p) = 1/3 + 1/3 = 2/3
"선택을 바꿀 경우의 전체 확률(overall probability)이 2/3이므로 선택을 바꾸는 것이 확률상으로 유리하다."라는 것이 된다.
전체 확률(overall probability)이 2/3라는 건 확률이 2/3라는 말과는 조금 다른데, 사회자의 편향 정도 q라는 변수를 추가하는 것으로 선택을 바꿀 경우의 확률이 2/3라고는 확정할 수 없게 되었지만 몬티 홀 문제처럼 q의 값이 특정되어 제시되지 않은 상황에선 0과 1 사이의 가능한 모든 q의 경우를 대입했을 때 전체적으로는 2/3라는 값이 나온다는 것이다.
사회자의 편향성을 p라는 변수로 추가했을 때 "선택을 바꿔서 이길 확률은 적어도 1/2이며(최대 1까지 올라갈 수 있다.), 선택을 바꿔 이기는 전체 확률(overall probability)은 여전히 2/3이다."
2) 지옥의 몬티(Monty from Hell):
참가자가 처음부터 자동차를 고른 경우에만 문을 바꾸도록 유도함.
→ 문을 바꾸면 항상 염소를 얻게 됨.
3) 독심술 몬티(Mind-reading Monty):
참가자가 절대 안 바꾸거나, 바꾸면 염소를 고를 경우에만 바꾸기를 제안함.
→ 문을 바꾸면 항상 염소
4) 천사 몬티(Angelic Monty):
참가자가 틀린 선택을 한 경우에만 바꾸기를 제안함.
→ 문을 바꾸면 항상 자동차
5) 무지한 몬티(Monty Fall 또는 Ignorant Monty):
문 뒤의 내용을 모르고, 우연히 자동차가 아닌 문을 무작위로 염.
→ 문을 바꾸면 절반의 확률로 자동차 획득
6) 사회자는 문 뒤의 내용을 알고 있음.
참가자가 고른 문과 다를 때만 무작위로 염소 문을 열고 바꾸기를 제안함.
→ 문을 바꾸면 절반 확률로 자동차 획득
7) 사회자는 참가자가 자동차를 골랐을 경우에는 100% 바꾸기를 제안,
그 외에는 50% 확률로 제안함.
→ 내시 균형에서 바꾸면 절반 확률로 자동차 획득
8) 사회자가 아예 문을 열지 않을 수도 있음.
→ 참가자는 무작위로 문 선택 후, 절대 바꾸지 않음
→ 참가자의 최소 승리 확률은 1/3, 방송국은 최대 1/3 확률로 손해
9) Deal or No Deal식 버전:
사회자가 참가자에게 문을 열게 한 후, 자동차가 나오지 않은 경우에만 바꾸기를 제안
→ 바꾸면 절반 확률로 자동차 획득
이러한 각 버전은 사회자의 행동이 확률에 어떤 영향을 미치는지를 보여주며, 몬티홀 문제의 본질은 사회자의 전략에 따라 결과가 완전히 달라질 수 있다는 것을 강조합니다.
'다시보는 통계학' 카테고리의 다른 글
| 일반화된 몬티 홀 문제(monty hall problem) 2 (0) | 2025.05.12 |
|---|---|
| 가중 절댓값 합(weighted absolute sum)을 최소로 만드는 방법(subgradient optimization) (0) | 2025.05.07 |
| 왜도(skewness)에 대한 오해 - 오른쪽으로 치우친 분포와 왼쪽으로 치우친 분포? (0) | 2025.04.21 |
| feature scaling을 위한 정규화(normalization) 기법들 (0) | 2025.04.12 |
| 상관관계는 인과관계가 아니다 - confounder model(교란변수 모델) (0) | 2024.04.20 |

