1. kernel
여러가지 뜻을 가지는 umbrella term: 다른 의미의 용어들을 모두 포괄하는 포괄적 의미를 가지는 용어
전체적으로는 kernel은 essential part, central part라는 뜻에서 여러 분야별로 파생됨
operating system에 쓰이는 것도 kernel

사전적으로 견과류, 씨앗, 알맹이,핵심

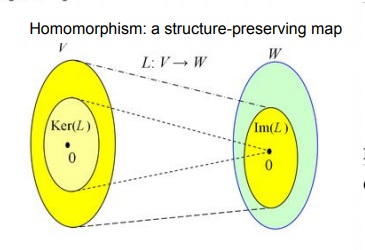
linear algebra에서 두 vector space V,W와 linear map L:V → W에 대하여 임의의 v ∈ V가 L(v)=0을 만족시키는
v의 집합을 Ker(L)이라고 부른다
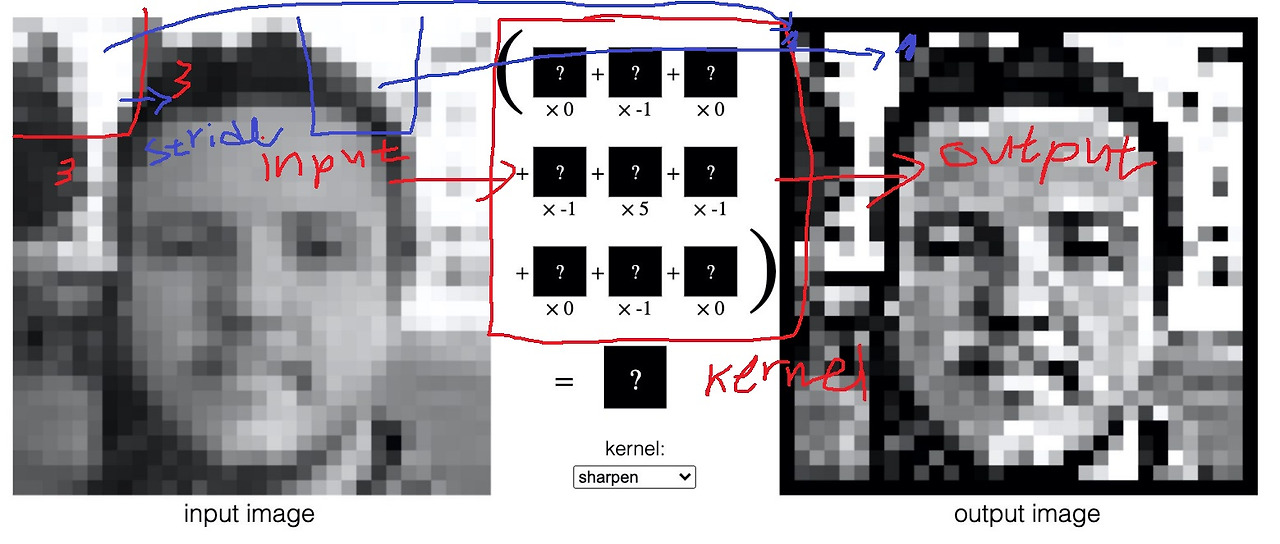
기타 image processing같은 경우 image를 변환시키는 filter를 kernel이라고 부른다는거 기억나는가
kernel을 input image위에서 stride하면서 convolution하여 output image를 뽑아냄
input 이미지 안에서 kernel을 통해 핵심적인 내용(essential part)을 요약하여 하나의 component로 mapping시킨다고 생각할 수 있음
2. kernel method
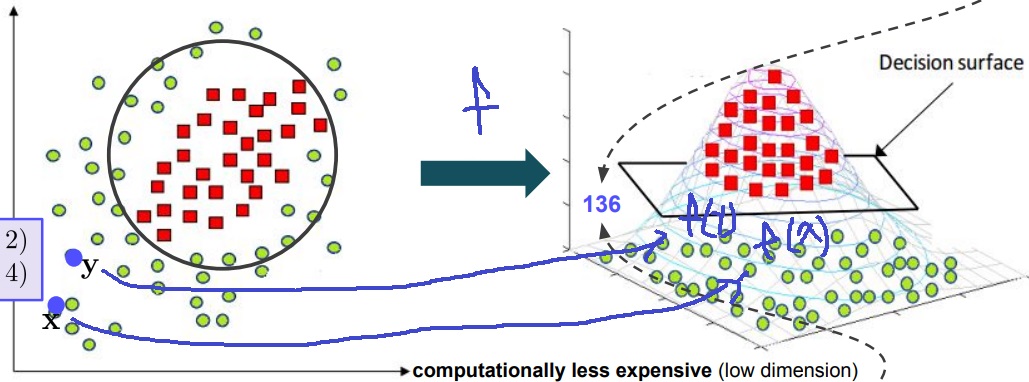
주어진 2차원 위의 데이터 point들에서 데이터의 category를 구분하고 싶은 상황

빨간색 점과 초록색 점을 classification하고 싶은 상황
x,y의 좌표는 각각 (1,2)와 (3,4)
kernel method의 핵심 아이디어는 이 데이터를 어떤 함수를 통해 고차원의 space로 보낸다면
반드시 그런것은 아니지만 저차원에서는 구분되지 않은 것들이 명확히 구분되는 경우가 있다는 것

위 그림과 같이 2차원 데이터를 3차원으로 보내보니 구분이 어렵던 것이 명확하게 구분지을 수 있게 된 상황
2차원에서도 구분이 쉬운데??
저차원에서 decision boundary를 명확히 긋기 어려웠는데 3차원의 경우 decision boundary를 명확히 그을 수 있다는 것임
어떻게 만들었는가??
2차원 데이터 x=(x1,x2)와 y=(y1,y2)에 대하여 3차원으로 보내는 함수를 f라고 한다면
$f(x) = (x_{1}, x_{2}, x_{1}^{2} + x_{2}^{2})$으로 정의하자.
2차원의 x,y 점들은 f(x)와 f(y)로 3차원의 어딘가에 mapping될 것임
함수 f를 이용해 고차원으로 mapping
다음으로 classification의 문제를 풀기위해 두 벡터 f(x)와 f(y)의 dot product를 계산하여 f(x)와 f(y)가 얼마나 비슷한지 similarity의 정도를 계산함
비슷하면 같은 category에 속하고 다르면 다른 category에 속하니까
x=(1,2), y=(3,4)이면 f(x)=(1,2,5)이고 f(y)=(3,4,25)이므로 <f(x),f(y)>=1*3+2*4+5*25=3+8+125=136

근데 예시는 2차원을 3차원으로 보내서 이게 계산이 복잡하다는게 와닿질 않지만
실제로 더욱 classification을 잘하려면 더욱 고차원으로 보내야한다
f(x)와 f(y)가 1000차원 넘어버리면 그 계산 비용이 생각보다 엄청 비싸다는거임
그런데 사실 계산과정을 조금 잘 본다면
$f(x)=(x_{1}, x_{2}, x_{1}^{2} + x_{2}^{2})$과 $f(y) = (y_{1}, y_{2}, y_{1}^{2} + y_{2}^{2})$
이렇게 계산되어 있는데 먼저 계산을 해보면 내적은 대응하는 원소끼리의 곱의 합이므로
$x_{1}y_{1} + x_{2}y_{2} + (x_{1}^{2} + x_{2}^{2})(y_{1}^{2} + y_{2}^{2})$
x1*y1+x2*y2은 x=(x1,x2)와 y=(y1,y2)의 내적과 같고
$(x_{1}^{2} + x_{2}^{2})(y_{1}^{2} + y_{2}^{2})$은 x=(x1,x2)와 y=(y1,y2) 각각의 L2 norm의 제곱의 곱과 같다
이 말은 x,y를 고차원 f(x),f(y)로 보내지 않고도 그냥 x,y만 안다면 <f(x),f(y)>를 계산할 수 있음을 의미한다
$K(x,y) = x*y + |x|^{2}|y|^{2}$을 $f(x) = (x_{1}, x_{2}, x_{1}^{2} + x_{2}^{2})$에 의해 주어지는 kernel function이라고 부른다

고차원으로 보내서 dot product를 하는 것보다 데이터를 고차원으로 보내기 전 저차원 상태에서 kernel을 이용해 계산하면
동일한 결과를 내면서도 computational cost를 상대적으로 줄일 수 있다는 것이 kernel method의 핵심
kernel의 의미와 유사??
불필요하게 고차원에서 계산하는 것보단 저차원에서 핵심적인 부분만 계산하여 동일한 결과를 내면서도 계산비용을 줄이는…
3. 또 다른 예시
kernel은 고차원에서의 dot product 결과와 동일한 값을 가지면서 저차원 상태에서 바로 계산할 수 있게 바꿔준 형태로 정의하면 된다…
이게 쉽진 않을듯? 찾는 방법이 있나
3차원에서 x=(x1,x2,x3)와 y=(y1,y2,y3)로부터 함수 f를 통해 9차원으로 보낼때 f(x)=(x1x1, x1x2, x1x3, x2x1, x2x2, x2x3, x3x1, x3x2, x3x3)로 정의한다면
$$f(x)f(y) = x_{1}^{2}y_{1}^{2} + x_{1}x_{2}y_{1}y_{2} + x_{1}x_{3}y_{1}y_{3} + x_{2}x_{1}y_{2}y_{1} + x_{2}^{2}y_{2}^{2} + x_{2}x_{3}y_{2}y_{3} + x_{3}x_{1}y_{3}y_{1} + x_{3}x_{2}y_{3}y_{2} + x_{3}^{2}y_{3}^{2} = (x_{1}y_{1} + x_{2}y_{2} + x_{3}y_{3})^{2}$$
만약 $K(x,y) = ((x1,x2,x3) * (y1,y2,y3))^{2}$으로 정의한다면?
$K(x,y) = (x1y1 + x2y2 + x3y3)^{2}$이므로 $$f(x)f(y) = x_{1}^{2}y_{1}^{2} + x_{1}x_{2}y_{1}y_{2} + x_{1}x_{3}y_{1}y_{3} + x_{2}x_{1}y_{2}y_{1} + x_{2}^{2}y_{2}^{2} + x_{2}x_{3}y_{2}y_{3} + x_{3}x_{1}y_{3}y_{1} + x_{3}x_{2}y_{3}y_{2} + x_{3}^{2}y_{3}^{2} = (x_{1}y_{1} + x_{2}y_{2} + x_{3}y_{3})^{2}$$ 를 계산하지 않아도 간단하게 동일한 결과를 얻는다
확실히 2차원에서 3차원으로 보낸 예시보다 계산량의 차이가 눈에 보임

'선형대수학' 카테고리의 다른 글
| vector space 개념 간단하게 (0) | 2024.08.24 |
|---|---|
| 여러가지 matrix decomposition(eigenvalue, singular value, CP, Tucker, non-negative,...) (0) | 2024.07.02 |
| gaussian elimination을 이용한 연립방정식의 해법 (0) | 2024.06.15 |
| linear transformation에 대해 간단하게 (0) | 2024.06.07 |
| 무어-펜로즈 역행렬(Moore–Penrose pseudoinverse matrix) (0) | 2022.01.17 |

