1. 무어펜로즈 역행렬(Moore–Penrose pseudoinverse matrix)
역행렬이 존재하지 않는 경우 대안으로 무어-펜로즈 역행렬을 생각할 수 있다.

행의 수와 열의 수에 따라 구하는 방식이 다르다
역행렬처럼 되돌리는 연산이 가능하다

np.linalg.pinv()는 무어 펜로즈 역행렬을 구해준다
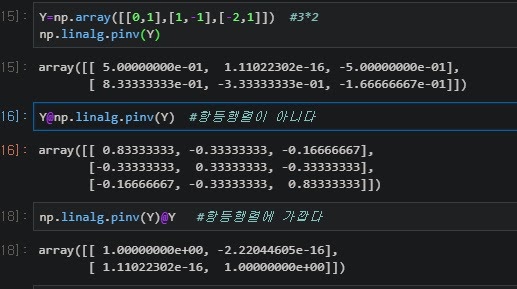
2. 연립방정식의 해법
연립방정식은 행렬의 선형변환을 이용해 간단히 나타낼 수 있다.
연립방정식은 일반적으로 식의 수와 변수의 수가 동일할 때 정확히 하나의 해를 갖지만
식의 수가 변수의 수보다 적거나 같으면 해가 무수히 많을 수 있다.
2-1) 무어펜로즈 역행렬을 이용한 해법
해가 무수히 많은 경우 무어 펜로즈 역행렬을 이용하여 무수히 많은 해 중 하나의 해를 구할 수 있다

2-2) 선형회귀분석에서의 응용
행의 수가 열의 수보다 많은 경우 선형회귀분석에서의 응용을 생각할 수 있다.
이런 경우는 데이터 수(=행의 수)가 변수의 수(=열의 수)보다 훨씬 많은 경우이다.
행렬이 평면 위 모든 데이터를 하나의 집합으로 묶어준다는 점을 상기하자.

데이터 집합 X에 $\beta$라는 계수벡터를 곱한 $X\beta$라는 선형모형으로 위 데이터를 설명하고 싶다.
어떤 $\beta$가 위 데이터 집합을 가장 잘 설명해주는가?
예측한 값 $X\beta$와 정답 y의 차이가 가장 작게되는 $\beta$가 데이터를 가장 잘 설명해주는 것.

3. sklearn과 무어 펜로즈 역행렬을 이용한 회귀분석
import numpy as np
X=np.array([[0,1],[1,-1],[-2,1]])
y=np.array([1,2,3])
x_test = np.array([[2,3],[3,1],[1,-1]])
데이터가 위와 같이 주어지면
#sklearn 이용
from sklearn.linear_model import LinearRegression
model = LinearRegression()
model.fit(X,y)
y_test = model.predict(x_test)
y_test
array([-3.,-2.,2.])
###무어펜로즈 역행렬
#절편항 없을 때
beta = np.linalg.pinv(X)@y
y_test = X@beta
y_test
array([-0.33333333, -0.66666667, -1.66666667])
#절편항 추가
X_=np.array([np.append(x,[1]) for x in X])
beta = np.linalg.pinv(X_)@y
y_test = np.array([np.append(x,[1]) for x in x_test])@beta
y_test
array([-3.,-2.,2.])
sklearn은 알아서 절편항을 추가시켜서 회귀분석시키지만
무어펜로즈 역행렬을 이용한 회귀분석을 수행할때는 절편항을 직접 추가해야한다.
np.append는 x에 절편항 [1]을 직접 추가시킴
728x90
'선형대수학' 카테고리의 다른 글
| gaussian elimination을 이용한 연립방정식의 해법 (0) | 2024.06.15 |
|---|---|
| linear transformation에 대해 간단하게 (0) | 2024.06.07 |
| 선형변환으로서의 행렬이 가지는 의미 (0) | 2022.01.12 |
| 행렬의 기본 연산들 (0) | 2022.01.11 |
| 행렬의 기하학적 의미 (0) | 2022.01.10 |

