gaussian elimination을 이용한 연립방정식의 해법

1. 3원 1차 연립방정식

 

미지수가 3개이고 각 미지수에 대해 차수가 모두 1차 방정식으로 이루어진 연립방정식은 3*3 matrix를 이용하여 표현할 수 있다

 

연립방정식을 행렬로 표현함

 

 

만약 행렬 A의 역행렬이 존재한다면 유일한 해 $x = A^{-1}b$를 이용해 구할 수 있다.

 

 

2. gaussian elimination

 

주어진 행렬의 rank를 구하는 방법

 

기본 행연산(elementary row operation)을 이용하여 주어진 행렬을 row echelon form으로 변환시키면 rank를 구할 수 있다

 

row echelon form이란

 

elementary operation을 통해서 1) 모든 원소가 0인 행(열)은 전부 밑에 존재 하고

 

2) 0이 아닌 원소가 있는 행(열)의 경우 가장 왼쪽에 있는 원소가 바로 위에 있는 행(열)은 바로 아래에 있는 행(열)보다 왼쪽에 있는 형태를 말한다.

 

위의 연립방정식의 행렬 A를 예로 들면 먼저 1행의 2배를 2행에 더해서 2행의 첫번째 원소가 0이 되도록 만든다

 

row echelon form으로 만드는 과정1

 

 

다음 3행의 첫번째 원소를 0으로 만들기 위해 1행의 -3배를 3행에 더해준다

 

row echelon form으로 만드는 과정2

 

 

다음 2번째 행과 3번째 행을 그대로 더해주면 3번째 행의 모든 원소가 0이 된다

 

row echelon form으로 만드는 과정3

 

 

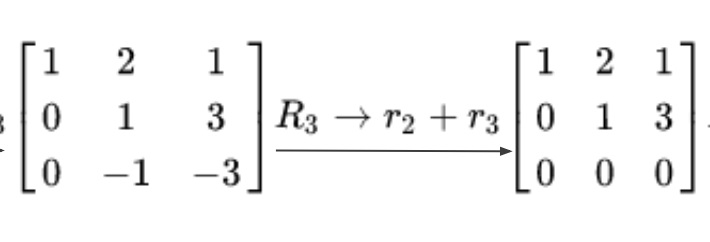
위와 같이 변환된 행렬을 원래 행렬의 row echelon form이라고 부른다.

 

 

0이 아닌 행의 수가 주어진 행렬의 rank가 된다. 위의 경우 행렬의 rank는 2가 된다

 

 

그러나 이렇게 변환된 row echelon form은 하나의 행렬에 대해 무수히 많아서 유일한 형태의 reduced row echelon form으로 바꾸기도 한다

 

 

reduced row echelon form은

 

1) row echelon form의 형태를 만족하면서 2) 0이 아닌 행의 가장 왼쪽에 있는 원소는 1이어야하고

 

가장 왼쪽에 있는 1인 원소는 바로 위에 있는 행은 바로 아래에 있는 행보다 왼쪽에 있어야하며(row echelon form)

 

3) 가장 왼쪽에 있는 1인 원소가 있는 열은 나머지 원소가 모두 0이어야 한다

 

현재 row echelon form에서 2행의 -2배를 1행에 더하면 1열이 1을 제외한 나머지 원소가 모두 0이고

 

2열도 1을 제외한 나머지 원소가 모두 0이어서 reduced row echelon form의 3번째 조건을 만족시킨다

 

최종 reduced row echelon form으로 만드는 과정

 

 

이렇게 만들면 주어진 행렬의 rank는 모든 원소가 0이 아닌 행의 수와 같고 위의 경우는 rank=2이며 행들이 linear dependent하다고 부른다

 

행렬은 full rank, square matrix의 차원의 수와 rank가 동일한 것이 아니면(linear dependent이면)

 

역행렬이 존재하지 않는다.

 

그래서 위에서 예시로 든 연립방정식은 행렬이 역행렬이 존재하지 않아 유일한 해 $x = A^{-1}b$가 존재하지 않는다