1. 용어
matrix나 tensor는 데이터 모델링을 위한 도구이다.
matrix가 2차원에 숫자를 나열해놓는 것이라면 tensor는 3차원에 숫자를 나열해놓는 데이터 모델링 도구

n*n square matrix에 대한 decomposition으로 1) eigenvalue decomposition, diagonalization은
$A = PDP^{-1}$ 혹은 A가 대칭행렬이면 $A = PDP^{-1} = PDP^{T}$
D는 대각행렬로 원소들이 eigenvalue이고 P는 eigenvector로 이루어진 행렬
eigenvalue decomposition은 다른 수식 $A = \sum_{}^{} \lambda uu^{T}$으로 나타내면 2) spectral decomposition이라고 부름
eigenvalue decomposition에 대한 일반화로 m*n matrix에 대한 decomposition인 3) singular value decomposition
singular value 원소가 main diagonal에 있는 $\sum_{}^{}$를 이용하여 $A = U\sum_{}^{}V^{T}$ 혹은
spectral decomposition처럼 $A = \sum_{}^{} \sigma uu^{T}$
singular value decomposition에서 4) truncated SVD와 principal component analysis가 이어짐.. SVD랑 관련되어 있다는 말
singular value decomposition이 tensor version으로 가면
동일한 tensor를 어떻게 분해하느냐에 따라 5) CP decomposition과 Tucker decomposition으로 이어짐
tucker decomposition이 조금 더 일반화된 버전이다?
tucker decomposition이랑 거의 똑같은데 약간 의미 차이가 있는게???(의미 차이 없는것 같은데) 6) high order singular value decomposition
그리고 이미 배웠던 7) depthwise separable convolution과 pointwise separable convolution이 사실은 CP decomposition이다?
neural network에서 발견한 8) network decoupling이 사실은 tensor decomposition들에 기반을 두고 있다
2. matrix decomposition
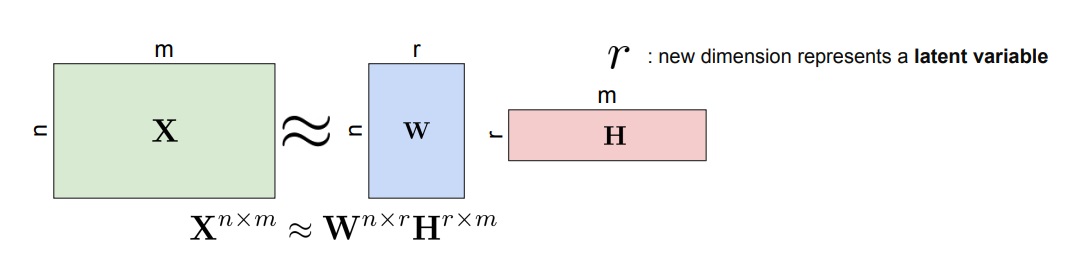
matrix decomposition이란 주어진 행렬 X를 또 다른 행렬 W, H의 곱으로 나타내는 방법
X와 WH는 equivalent일 수 있지만 거의 보통은 approximation시켜서 사용함
3. 예시로 이해하는 matrix decomposition
예를 들어 추천시스템의 UV 분해나 singular value decomposition
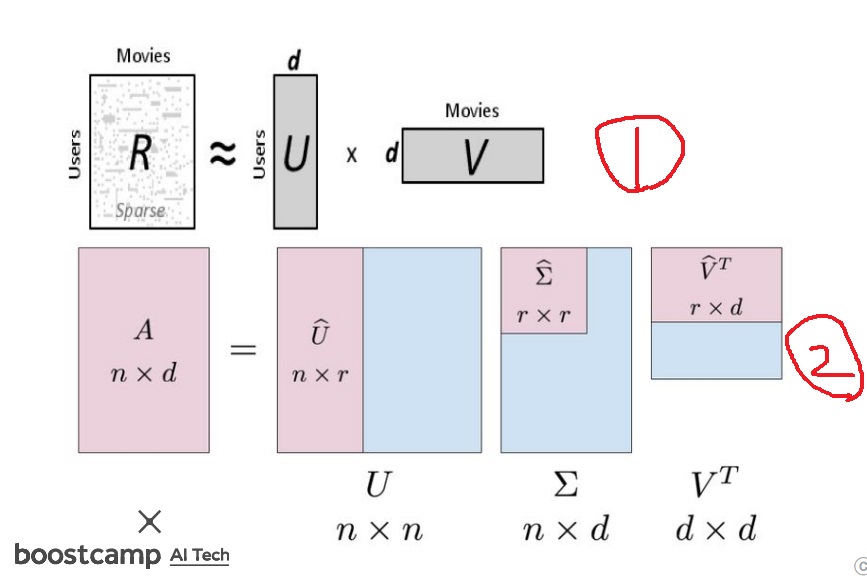
1번은 유저별 영화에 대한 평점 matrix R을
영화에 대한 평점에 직접적인 영향은 아니지만 어디선가는 영향을 미치는 잠재변수 d를 이용하여
유저와 d의 관계를 나타내는 행렬 U와 d와 영화 평점의 관계를 나타내는 행렬 V를 이용하여 UV로 근사시키는 방법이 UV decomposition
2번은 singular value decomposition으로 주어진 n×d행렬 A를 $A = U \sum_{}^{} V^{T}$로 나타내는 방법
singular value matrix같은 경우 main diagonal을 제외한 나머지 원소는 모두 0이므로
0인 부분(혹은 더 근사시키고 싶다면 0이 아닌것도 조금 포함해서)을 잘라버려서
$A \approx \hat{U} \hat{\sum_{}^{}} \hat{V}^{T}$로 근사시키는 방법이 truncated SVD
4. eigenvalue decomposition
행렬이라는 것은 linear transformation
주어진 행렬 A의 eigenvector는
행렬 A라는 linear transformation을 하더라도 길이만 늘어나도(길이가 줄어들어도) vector의 방향은 그대로인 vector
길이가 변하는 양은 eigenvalue라고 부름


파란색, (분홍색도 마찬가지인데???)은 변환을 해도 방향이 여전하고 길이는 그대로 저것이 행렬의 eigenvector
5. 수학적으로 eigenvalue decomposition이란
square matrix A의 eigenvector로 이루어진 행렬 P와 대응하는 eigenvalue들을 대각원소로 하는 대각행렬 D를 이용하여 $A = PDP^{-1}$로 나타내는 것
만약 행렬 A의 모든 원소가 실수이고 대칭행렬이면 $P^{-1} = P^{T}$여서 $A = PDP^{-1} = PDP^{T}$로 나타낼 수 있다

6. singular value decomposition
eigenvalue decomposition이 square matrix에 대한 것이라면 이것의 일반화로 임의의 m×n행렬에 대한 것

수학적으로 A의 singular value를 대각원소로 가지는 행렬 ∑과 대응하는 singular vector들로 이루어진 square matrix U, V를 이용하여 $A = U \sum_{}^{} V^{T}$로 나타내는 것
∑ 의 경우 main diagonal에는 singular value가 있고 나머지는 0인 원소를 가지는 행렬이고 그림에서 색깔별로 구별되어 있는데
(1,1)원소가 singular value가 가장 크고 다음이 (2,2), 그 다음이 (3,3)으로 크기가 점점 작아진다는 표시임
m과 n의 크기에 따라 $A = U \sum_{}^{} V^{T}$으로 똑같지만 행렬 모양이 달라지니까 그림도 두가지로 표현
7. singular value decomposition의 기하학적 의미
orthogonal matrix에 의한 transformation은 rotation을 나타낸다
diagonal matrix에 의한 transformation은 scaling을 나타낸다
행렬 $M = U \sum_{}^{} V^{T}$과 데이터 x에 대하여 $Mx = U \sum_{}^{} V^{T}x$이므로 데이터 x를 M으로 변환한것은 x를 $V^{T}$로 변환하고 ∑로 변환하고 U로 변환한 것과 동일하다
따라서 행렬 $M = U \sum_{}^{} V^{T}$에 대하여 두 벡터를 M으로 한번에 transformation하는 것은
$V^{T}$에 의해 rotation을 먼저 하고 ∑ 에 의해 scaling을 하고 U에 의해 rotation을 순차적으로 하는 것과 같다

모든 원소가 실수인 행렬이면 conjugate transpose는 transpose와 같아서 V*=$V^{T}$로 사용할 수 있다
8. singular value와 eigenvalue의 관계
수학적으로 $M = U \sum_{}^{} V^{T}$이면 transpose하면 $M^{T} = V (\sum_{}^{})^{T} U^{T}$
수학적으로 U와 V는 unitary matrix인데 M의 모든 원소가 실수이면 orthogonal matrix여서 $UU^{T} = U^{T}U = I$이고 $VV^{T} = V^{T}V = I$를 만족시킨다
따라서 $MM^{T} = U \sum_{}^{} V^{T} V (\sum_{}^{})^{T} U^{T} = U \sum_{}^{} (\sum_{}^{})^{T} U^{T}$
비슷하게 $M^{T}M = V (\sum_{}^{})^{T} \sum_{}^{} V^{T}$
∑가 main diagonal이 singular value이고 나머진 모두 0인 행렬이므로
$\sum_{}^{} (\sum_{}^{})^{T}$나 $(\sum_{}^{})^{T} \sum_{}^{}$는 main diagonal이 singular value의 제곱이고 나머진 0인 대각행렬이 된다.

그래서 $(\sum_{}^{})^{T} \sum_{}^{} = (\sum_{}^{})^{2}$ 이라고 표현하기도 하고 이 행렬은 square matrix여서 대각행렬이고
최종 결과 $MM^{T}$이 모든 원소가 실수이고 symmetric이므로
(그냥 계속 복소수를 가정하지 않고 있어서 그렇고 $MM^{T}$은 transpose해도 $MM^{T}$이니까 symmetric임)
$MM^{T} = U (\sum_{}^{})^{2} U^{T} = PDP^{-1} = PDP^{T}$으로 행렬 A가 $MM^{T}$인 eigenvalue decomposition과 동일함
그래서 singular value decomposition이 eigenvalue decomposition의 일반화인 것이고
행렬 A의 singular value의 제곱이 $AA^{T}$나 $A^{T}A$의 eigenvalue와 동일하다
(A의 singular value랑 A의 eigenvalue랑은 관계없어… 주의)

9. truncated singular value decomposition(principal component analysis)
singular value decomposition을 보면 $A = U \sum_{}^{} V^{T}$에서
∑의 경우 main diagonal에는 singular value가 있고 나머지는 0인 원소를 가지는 행렬이면서 square matrix도 아니다
그래서 ∑ 에서 필요없는 0인 부분을 지워버리고 singular value 있는 부분만 가지고 와서 만든 diagonal matrix $\hat{\sum_{}^{}}$를 이용하여 singular value decomposition을 한 것을 truncated SVD라고 부른다

특히 singular value를 전부 남기고 0인 부분을 지워도 결과가 여전히 원래 행렬과 동일하다
그런데 때로는 singular value가 너무 많아서 여전히 computational cost가 많을 수 있다
그리고 ∑의 singular value는 (1,1)부터 내림차순으로 구성할 수 있다는 것이 수학적으로 알려져있다
그래서 특히나 중요한 singular value만 남기고 필요없는(크기가 작은) singular value의 일부를 지워서
원래 행렬에 approximation할 수 있는데 principal component analysis라고 부른다
핵심적인 singular value가 r개라고 한다면(r<n<m을 가정)
$A = U \sum_{}^{} V^{T}$로 분해하는 대신에 $A \approx \hat{U} \hat{\sum_{}^{}} \hat{V}^{T}$로 근사시킬 수 있다는 것이 truncated SVD 혹은 principal component analysis

10. 또 다른 decomposition들
바로 위에서 설명한 것이 truncated singular value decomposition
singular value decomposition을 tensor 버전으로 확장하면 CP decomposition이나 Tucker decomposition이 된다
주어진 행렬을 음이 아닌 원소들로만 포함된 행렬 W, H의 곱으로 approximation하는 방법을 non negative matrix factorization이라고 부른다.
이미지 데이터 같은 경우 pixel이 음수가 아닌 tensor로 표현되므로 non negative matrix factorization에 의해 음수가 아닌 성질을 잘 보존하면서 feature를 추출할 수 있다

'선형대수학' 카테고리의 다른 글
| low rank approximation 개요 간단하게 (0) | 2024.08.31 |
|---|---|
| vector space 개념 간단하게 (0) | 2024.08.24 |
| kernel method에 대해 간단하게 (0) | 2024.06.20 |
| gaussian elimination을 이용한 연립방정식의 해법 (0) | 2024.06.15 |
| linear transformation에 대해 간단하게 (0) | 2024.06.07 |

