linear transformation에 대해 간단하게

matrix나 tensor는 linear transformation이다.

 

linear transformation 예시1

 

 

 

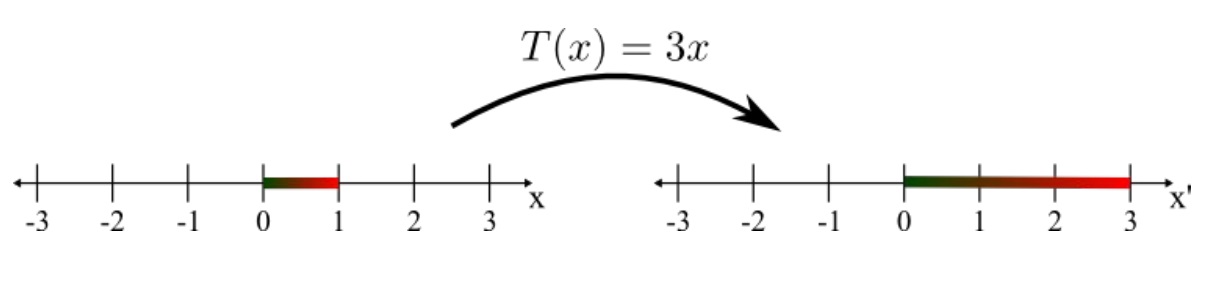
1차원의 [0,1]의 선분을 linear transformation T(x)=3x를 통해 변환하면 3배 늘어난 선분 [0,3]이 된다

 

linear transformation 예시2

 

 

 

주어진 2차원의 정사각형 ABCD를 linear transformation

 

 

 

 

을 통해 변환하면 2배 늘어나고 회전된 정사각형 A’B’C’D’이 된다

 

linear transformation 예시3

 

 

 

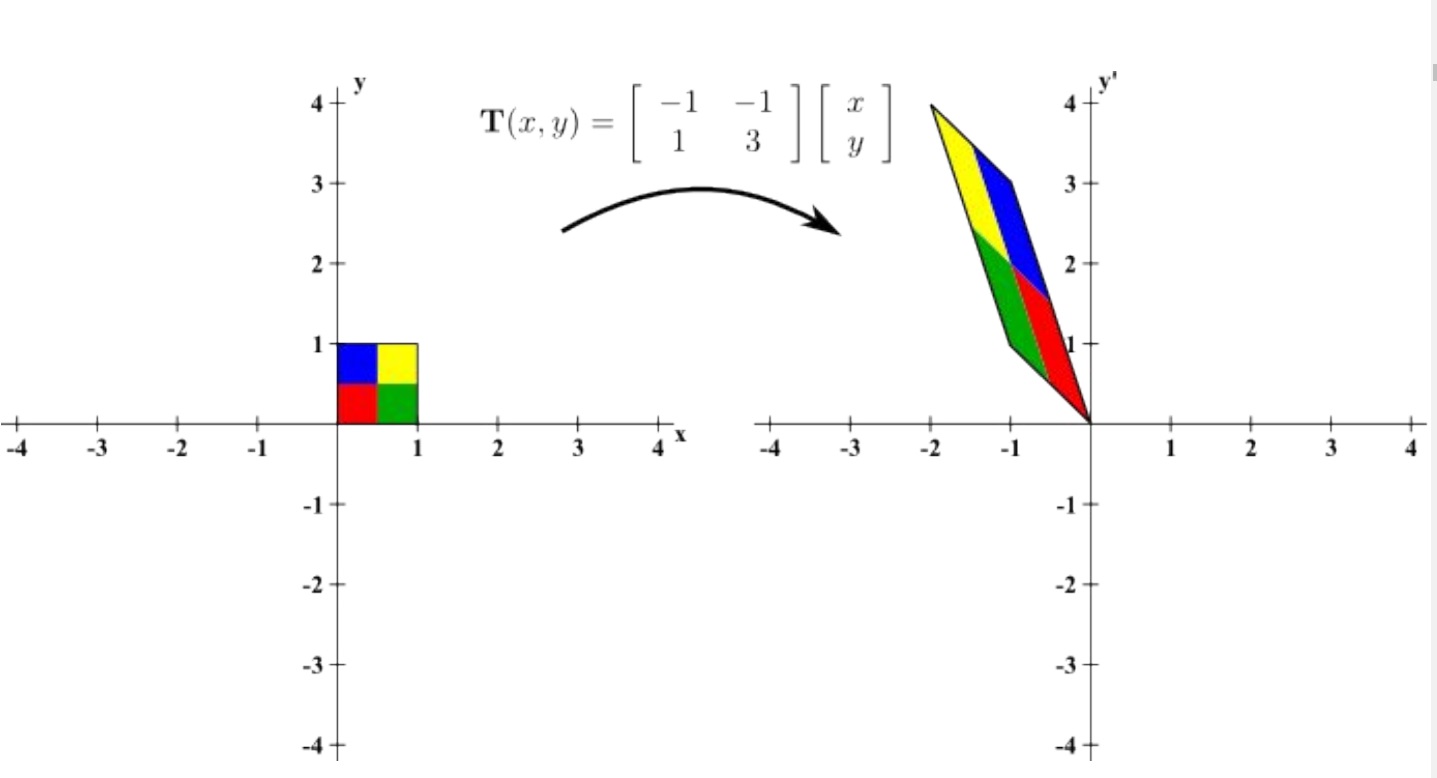
조금 더 복잡하게 주어진 정사각형을 늘리거나 회전시키거나 비틀어버리거나 하더라도 linear transformation

 

수학적으로 vector space V,W에 대하여 f: V → W가 linear map이라는 것은

 

임의의 vector u,v ∈ V와 scalar c가 

 

$f(u+v)=f(u)+f(v)$ , $f(cu)=cf(u)$를 모두 만족시키는 것이다.