신경망은 무엇이고 딥러닝에서 활성화함수를 왜 사용하는가?

1. 신경망(neural network)

 

보통 인간의 뇌에서 애매하게 영감받아 만들어낸 컴퓨팅 시스템?이라고 말한다

 

왜 신경망이 성능이 좋을까?

 

인간의 뇌를 모방해서 잘 작동한다?

 

꼭 그렇지는 않다

 

왜냐하면 역전파 알고리즘이 우리 뇌에서 작동하는가? 그렇지는 않잖아

 

수학적으로 신경망은 affine transformation(행렬 변환)과 nonlinear transformation의 순차적이고 반복적인 곱의 형태로 구해지는 함수 근사 모형이다.

 

신경망은 선형모형과 비선형함수인 활성화함수의 합성함수이다.

 

활성화함수는 기본적으로 선형모형의 결과를 원하는 방향으로 해석하게 도와준다.

 

활성화함수를 쓰지 않으면 딥러닝은 선형모형과 차이가 없다

 

그림1. 신경망 대략적인 구조

 

2. linear neural network

 

일반적으로 잘 아는 기본 선형 뉴럴 네트워크의 모형

 

그림2. 선형 신경망 모형의 기본

 

loss를 최소화하는 것이 목적인데

 

사실 선형 신경망 모형에서 loss를 최소화하는 w,b의 analytic function이 이미 잘 알려져있다(아마 최소제곱법 함수?)

 

그런데 데이터 수나 모수 수가 많으면 계산이 어렵다.

 

그래서 역전파 알고리즘으로 loss를 줄일 수 있다.

 

 

3. gradient algorithm

 

역전파 알고리즘은? loss를 가중치로 편미분하여 역으로 전달해나가는 과정

 

그림3. loss에 대한 parameter로 편미분

 

gradient algorithm은 parameter가 어느 방향으로 움직일 때 loss가 줄어드는지 확인하여

 

그 방향으로 parameter를 update 해나가는 과정이다.

 

그림4. gradient algorithm에 의한 parameter update 수식

 

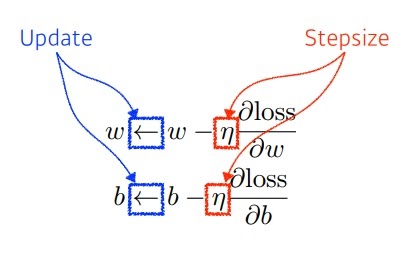
stepsize를 적절하게 선택하는 것이 중요한데

 

너무 크면 학습이 안되고 너무 작아도 학습이 안된다

 

 

4. 어떻게 쌓아야 deep learning일까?

 

행렬은 두 벡터 공간 사이의 선형변환이다.

 

즉, linear neural network는 행렬로 나타낼 수 있다.

 

deep learning이라는 말에서 linear neural network를 여러개 사용하면 deep learning이 되는 것인가?

 

이러한 행렬변환을 계속해서 곱해나가는 과정을 하면 deep learning이 되는 것일까?

 

그림5. 행렬변환을 계속해서 곱한다면?

 

행렬변환을 아무리 곱해서 쌓아나가도

 

결국엔 하나의 행렬이나 마찬가지기 때문에 사실상 1층 neural network나 다름 없다

 

그림6. 비선형함수의 필요성

 

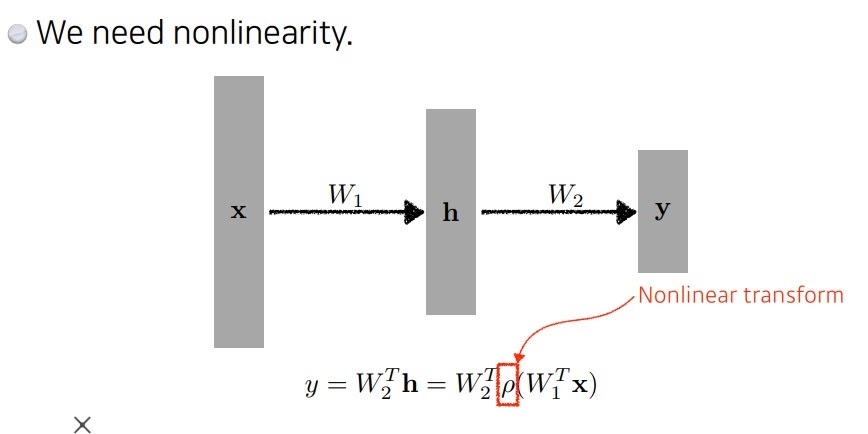
비선형함수를 중간에 사용함으로써 층을 깊게 이어나갈 수 있다

 

선형+비선형>>1차 output>>선형+비선형>>>2차 output >>>

 

 

5. activation function

 

딥러닝에서 비선형 함수로 사용하는 activation 함수

 

그림7. 여러가지 activation function

 

 

6. universal approximation theorem

 

hidden layer가 하나가 있는 2층 neural network는 우리가 생각하는 대부분의 continuous 함수를 모두 근사시킬 수 있다.

 

그러나 가능하다는 것만 보장하지 그런 neural network를 어떻게 찾는지를 알려주는 것은 아니다.

 

결국에는 deep learning을 만들 수 밖에 없다.

 

 

 

7. Multi Layer Perceptron

 

선형함수에 비선형함수를 여러번 결합한 신경망

 

그림8. multi layer perceptron의 구조

 

 

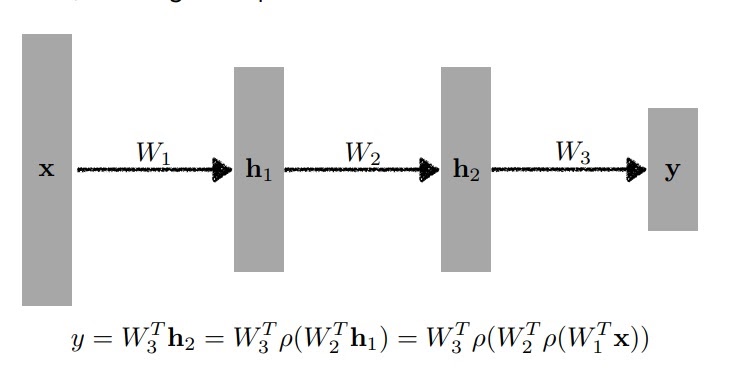
신경망에서 input을 넣어 output을 얻는 계산과정을 forward propagation이라 한다.

 

그림9. forward propagation의 대략적인 수식

 

층을 깊게 쌓을수록 목적함수를 근사시키는데 필요한 뉴런의 수가 훨씬 빨리 줄어들어 효율적으로 학습이 가능함

 

 

그러나 층이 깊다고해서 조금 더 복잡한 함수를 근사시키는데 좋을 순 있지만 모형 최적화에는 많은 노력이 필요하다.