여러가지 optimizer의 원리

1. Optimizer

 

일반적으로 최적화 알고리즘으로 gradient descent method를 사용하는데 손으로 하기도 어렵고 귀찮다.

 

그래서 요즘 컴퓨터가 다 계산해주는데 어떻게 계산해주느냐에 따라 여러가지 종류가 나왔다.

 

 

2. Gradient Descent

 

일반적인 gradient descent 방법

 

그림1. gradient descent 수식

 

가중치에 그래디언트와 learning rate의 곱을 빼면서 update한다.

 

문제는 learning rate를 어떻게 잡아야할지가 고민이다.

 

너무 크게 잡자니 overshooting으로 학습이 안되는 현상이 나타나고 너무 작게 잡자니 너무 학습이 느림

 

 

3. Momentum

 

그림2. momentum 수식

 

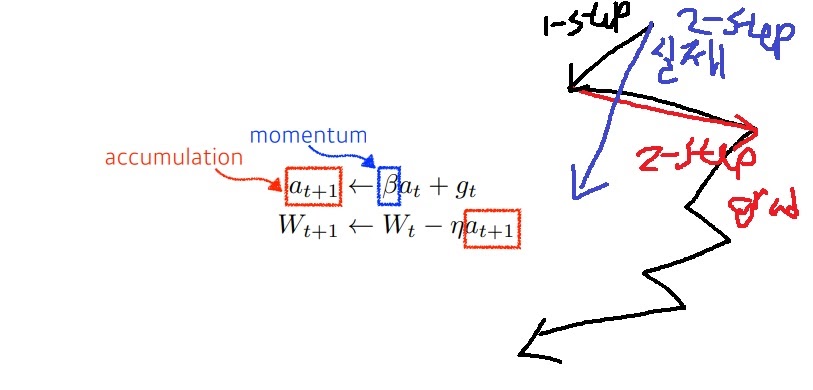
어떻게 하면 최적치에 더 빨리 갈수 있을까라는 생각에 이전 gradient의 정보를 가진 momentum을 이용하자.

 

이전에 gradient 방향이 최적치에 가까이 가는 중이라고 기대하기 때문이다.

 

2-step에 진행방향을 단순히 2step의 gradient방향으로 가지말고 이전 1-step gradient와 2-step gradient의 적절한 벡터합 방향으로 가자.

 

gradient 방향을 전체적으로 유지하면서 기존보다 학습이 잘되었다.

 

그런데 사실 큰 문제가 있었는데

 

그림3. momentum의 문제

 

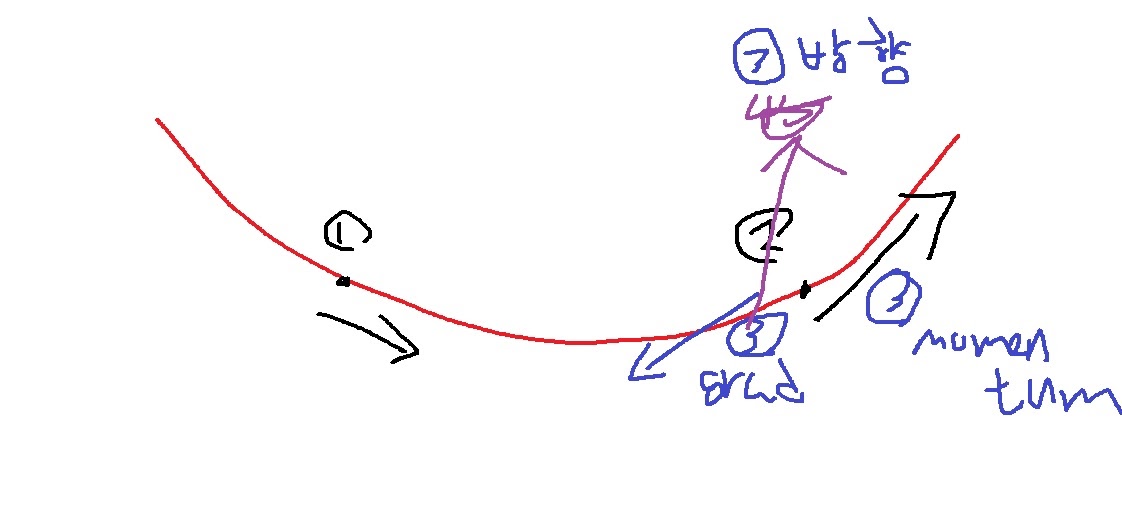
위와 같이 1번에 국소점의 왼쪽에 있었다가 2번에 국소점의 오른쪽에 가게 되었는데

 

3step에 내려가야하지만 이미 gradient가 올라가는 쪽이어서 3step momentum 방향이 올라가는 느낌이라

 

gradient와의 합이 여전히 올라가는 방향을 가리킬 가능성이 있다

 

그래서 국소점을 도달하지 못하는 경우가 생겼다

 

 

4. Nesterov Acclerated Gradient

 

그러면 일단 그 곳에 간 뒤에 gradient를 계산하자는 새로운 방법이 제안되었다.

 

그림4. Nesterov Acclerated Gradient 수식

 

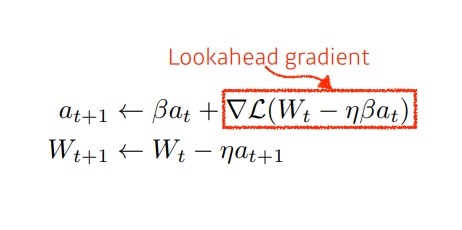
그러면 이제 MOMENTUM이 가지는 문제를 어느정도 해결할 수 있었다.

 

그림5. Nesterov Acclerated Gradient의 움직임

 

위와 같이 2번에 도달했을 때 다음 STEP은 3번처럼 내려가는 방향인데

 

MOMENTUM이면 올라갔지만 NGA방법은 일단 내려간 뒤에 gradient를 계산하여 최솟값에 도달할 수 있었다

 

momentum과의 직관적인 차이는

 

그림6. momentum과의 차이

 

5. Adagrad

 

이번에는 learning rate를 어떻게 조절했는지 알아보자.

 

Adagrad는 gradient의 제곱 누적합을 이용하여 learning rate에 벌점을 부여함.

 

너무 크게 변하는 경우는 큰 벌점을 주어 적게 변화시키고 너무 덜 변하는 경우는 작은 벌점으로 빠르게 변화시키고자 함

 

그림7. adagrad의 수식

 

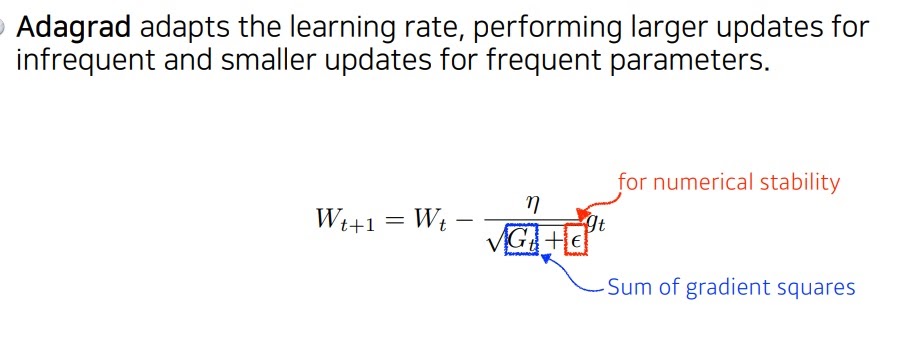
stability는 분모가 0이 되는 것을 방지함.

 

adagrad말고도 분모가 0이 되는 것을 방지하는 것은 여러 이론에 자주 사용함

 

당연히 문제가 있었는데 $G_{t}$가 시간이 오래 지나면 무한으로 가서 learning rate가 0이 되니 학습이 안된다.

 

 

6. Adadelta

 

Adadelta는 $G_{t}$의 계속되는 증가를 막고자 exponential moving everage 방법을 이용하였다.

 

그림8. adadelta의 수식

 

특히 learning rate가 없다는 부분이 재미있다

 

가중치의 미분 정보를 포함시키는 항을 분자에 추가하였음

 

그런데 learning rate가 없어서 쉽게 조정할 수 있는 부분이 없으니 잘 쓰지 않는다.

 

 

7. RMSprop

 

RMSprop는 geoff hinton이 강의에서 그냥 써보니까 잘 되더라는 식으로 이야기한 방법이다.

 

근데 실제로 잘되긴함

 

위와 같은 adadelta 방식에서 learning rate만 추가하였다

 

그림9. RMSprop의 수식

 

8. Adam

 

adam은 그동안 나온 방법을 모두 고려하여,

 

이전 gradient의 정보를 가지는 momentum방식과

 

learning rate를 adaptive하게 조절하는 gradient의 exponential moving average 방법을 모두 혼합하였다.

 

그림10. Adam의 수식

 

가장 효과적이고 지금도 가장 잘 쓰는 방식

 

위에서 실질적으로는 $\epsilon$을 적절하게 선택하는 것이 성능 향상에 중요하다고 한다

 

$1-\beta_{1}^{t}$뭐라 뭐라 된 항은 unbiased 시키는 항이라고 수학적으로 증명된 부분