1. 그래디언트 벡터(gradient vector)
어떤 변수 벡터 $x=(x_{1}, x_{2}, x_{3}, .... , x_{n})$에 대하여
함수 $f(x)$의 gradient vector는 각 변수별로 편미분한 성분을 원소로 갖는 벡터
\[\bigtriangledown f(x) = (\frac{df(x)}{x_{1}}, \frac{df(x)}{x_{2}}, ... , \frac{df(x)}{x_{n}})\]
gradient vector $\bigtriangledown f(x)$는 점 x에서 함수 f가 가장 빠르게 증가하는 방향을 가리킨다.
당연하지만 -gradient vector인 $-\bigtriangledown f(x)$은 점 x에서 함수 f가 가장 빠르게 감소하는 방향을 가리킨다
2. 편미분(partial differentiation)

$e_{i}$는 $i$번째 원소가 1인 단위벡터이고 편미분이란 $X$의 $i$번째 원소의 변화율을 계산하는 것
해당하는 변수를 제외한 나머지는 상수로 취급하고 미분
요새는 다 컴퓨터가 계산해줌
다음은 $x^{2}+2xy+3+cos(x+2y)$를 $x$로 편미분한 도함수를 구하는 코드
import sympy as sym
from sympy.abc import x,y
sym.diff(sym.poly(x**2+2*x*y+3)+sym.cos(x+2*y),x)
2x+2y-sin(x+2y)
3. 경사하강법 알고리즘(gradient descent algorithm)
3-1) 초기값 $x$를 선택한다
3-2) 목적함수 $f(x)$에 대하여 $x$의 gradient값 $\bigtriangledown f(x)$을 계산한다
3-3) 경사하강법에 의하여 새로운 x값으로
\[x^{(n+1)}\leftarrow x^{(n)}-\lambda \bigtriangledown f(x)\] 갱신한다
3-4) 여기서 학습률 $\lambda$는 적절하게 선택해야 한다.
학습률이 매우 크면 그래디언트 벡터의 길이가 매우 커져서 목적함수가 매우 빠르게 감소한다.
학습률이 매우 작으면 그래디언트 벡터의 길이가 매우 작아져 목적함수가 아주 느리게 감소한다
그런데 아주 빠르게 감소하다가 보면 극솟값을 놓칠 수도 있다
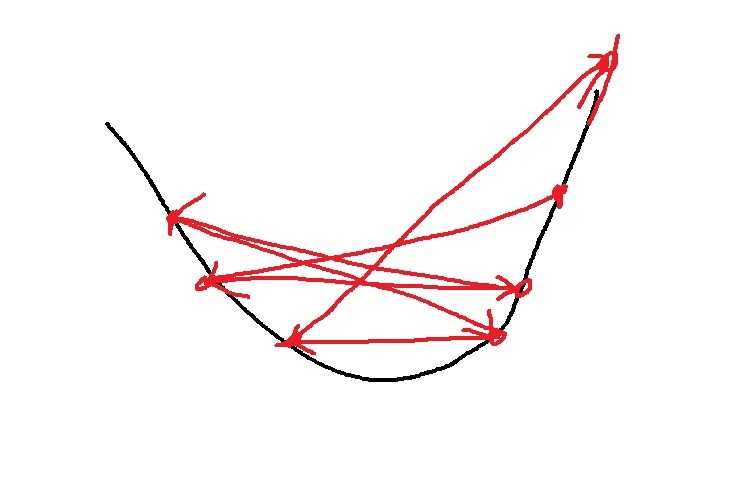
위 그림3은 학습률이 너무 커서 극솟점을 찾지 못하고 튕겨나가는 현상
3-5) 적절하게 학습률을 선택했으면 경사하강법을 제대로 수행하게 되며 grdient vector가 0에 가까우면 종료한다
수학적으로는 0이 나와야 극점이지만 컴퓨터 계산 오차로 인해 0이 거의 나오지 않는다
3-6) 그러므로 적절히 실험자가 지정한 값보다 작으면 종료하는 것으로 한다
4. 단변량 경사하강법을 구현한 코드
import numpy as np
import sympy as sym
from sympy.abc import x,y
def func(val):
fun = sym.poly(x**2+2*x+3
return fun.subs(x,val),fun #subs는 x에 val이라는 값으로 대체한다는 의미
def func_gradient(fun,val):
_,function=fun(val)
diff = sym.diff(function,x)
return diff.subs(x,val),diff
def gradient_descent(fun,init_point,lr_rate=1e-2,epsilon=1e-5):
cnt = 0
val = init_point
diff,_=func_gradient(fun,init_point)
while np.abs(diff)>epsilon:
val = val - lr_rate*diff
diff,_ = func_gradient(fun,val)
cnt+=1
print("함수:{}, 연산횟수:{}, 최소:({},{})".fotmat(fun(val)[1],cnt,val,fun(val)[0]))
gradient_descent(fun=func,init_point=np.random.uniform(-2,2))
함수:Poly(x**2+2*x+3,x,domain='ZZ'),연산횟수:603,최소:(-0.999995046679024,2.000000000024)
subs(x,y)는 x를 y로 대체한다는 의미
np.abs(diff) >epsilon으로 그래디언트 벡터의 크기가 지정한 1e-5보다 작으면 반복을 종료
여러 return값중 앞으로 필요없는 값은 _으로 받아서 지워버리고 원하는 값만 받아올 수 있음
5. 다변량 경사하강법을 구현한 코드
import numpy as np
import sympy as sym
from sympy.abc import x,y
def eval_(fun,val):
val_x, val_y = val
fun_eval = fun.subs(x,val_x).subs(y,val_y)
return fun_eval
def func_multi(val):
x_,y_=val
func = sym.poly(x**2+2*y**2)
return eval_(func,[x_,y_]),func
def func_gradient(fun,val):
x_,y_=val
_,function = fun(val)
diff_x = sym.diff(function,x)
diff_y = sym.diff(function,y)
grad_vec = np.array([eval_(diff_x,[x_,y_]),eval_(diff_y,[x_,y_])],dtype=float)
return grad_vec,[diff_x,diff_y]
def gradient_descent(fun, init_point, lr_rate=1e-2, epsilon=1e-5):
cnt = 0
val = init_point
diff,_ = func_gradient(fun,val)
while np.linalg.norm(diff) > epsilon:
val = val - lr_rate*diff
diff,_ = func_gradient(fun,val)
cnt+=1
print('함수:{}, 연산횟수:{}, 최소:({},{})'.format(fun(val)[1],cnt,val,fun(val)[0]))
pt = [np.random.uniform(-2,2),np.random.uniform(-2,2)]
gradient_descent(fun=func_multi,init_point=pt)
함수:Poly(x**2+2*y**2,x,y,domain='ZZ'), 연산횟수:574, 최소:([4.97220022e-06 -5.77458718e-12],2.47227749817380E-11)
그래디언트 벡터의 norm이 0에 가까워지면 반복을 종료하는 조건을 둔다
'딥러닝 > 딥러닝 기초' 카테고리의 다른 글
| 신경망은 무엇이고 딥러닝에서 활성화함수를 왜 사용하는가? (0) | 2021.12.31 |
|---|---|
| 여러가지 활성화함수(activation function) (0) | 2021.12.31 |
| 미분계수에 대하여 (0) | 2021.12.29 |
| gradient descent method 핵심요약 (0) | 2021.12.29 |
| 여러가지 regularization 기법 (0) | 2021.12.26 |

