미분계수에 대하여

1. 미분계수의 정의

 

변수의 움직임에 따른 함숫값의 변화를 측정

 

변화율, 기울기의 극한값

 

함수 f(x)위의 한 점 (x,f(x))의 접선의 기울기

 

기본적으로 함수의 모양이 매끄러워야 미분가능

 

그림1. 미분계수의 정의

 

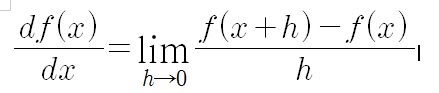
미분계수의 모임이 도함수

 

도함수를 요즘에는 컴퓨터가 다 계산해준다

 

python의 sympy를 이용하여 함수식을 다룰수 있고 도함수를 구할 수 있다

 

그림2. python을 이용하여 도함수를 구한 모습

 

2. 미분계수의 성질

 

한 점에서 접선의 기울기를 알면 어느 방향으로 점을 움직여야 함숫값이 증가하는지, 감소하는지 알 수 있다.

 

함숫값을 증가시키려면 미분값을 더하고 감소시키려면 미분값을 빼주면 된다.

 

2차원이면 눈으로 쉽게 보이지만 앞으로 고차원을 다루기 때문에 잘 이해하는 것이 중요함

 

 

3. 미분에 대하여

 

너무 오랜만에 미분 했는지 아주아주 기본적인 부분에서 실수했다

 

 

저게 성립하는게 자명한데 처음에 어떻게 했는지 기억나냐?

 

분자에 a를 빼먹고 안씀 ㅡㅡ

 

 

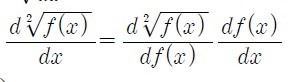
루트함수 미분과 겹쳐서 합성함수의 미분에서 첫번째 걸 빼버리고 df(x)/dx만 써버리는 어처구니 없는 실수

 

다시 예열했으니까 너무 자책하지는 말자고

 

 

4. 경사상승법(gradient ascent)

 

미분값을 더해나가 함수의 극댓값(local maximum)을 찾는 방법

 

목적함수를 최대화하는 방법

 

그림3. f'(x)<0인 경우 경사상승법의 원리

 

f’(x) < 0이므로 x에 미분값 f’(x)를 더하면 왼쪽으로 이동함

 

미분값을 더했더니 함숫값이 증가하면서 극댓값을 찾아나가고 있음

 

그림4. f'(x)&gt;0인 경우 경사상승법의 원리

 

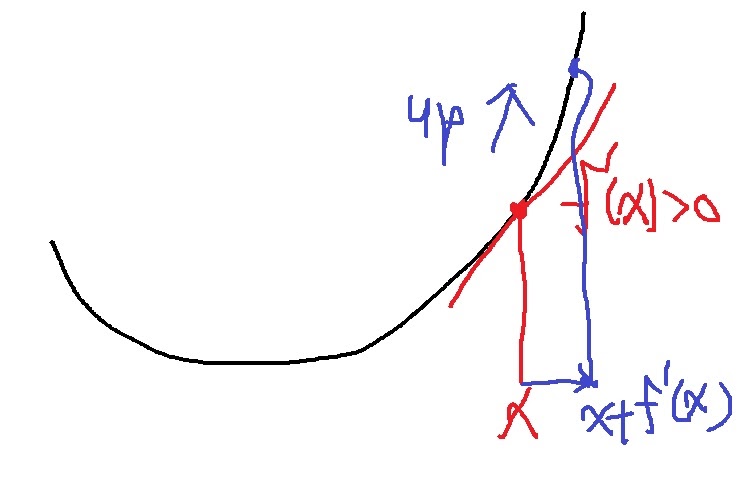
f’(x) >0 인 경우 x에 미분값 f’(x)를 더하니 오른쪽으로 이동함

 

미분값을 더했더니 함숫값이 증가하면서 극댓값을 찾지 못하고 있음

 

당연히 없으니까 못찾지

 

 

5. 경사하강법(gradient descent)

 

미분값을 빼나가 함수의 극솟값(local minimum)을 찾아나가는 방법

 

목적함수를 최소화하는 방법

 

그림5. f'(x) &lt;0인 경우 경사하강법의 원리

 

f’(x)가 음수이므로 미분값을 빼면 오른쪽으로 이동함

 

미분값을 뺐더니 함숫값이 감소하지만 극솟값을 찾지 못함

 

그림6. f'(x)&gt;0인 경우 경사하강법의 원리

 

f’(x) >0이므로 미분값을 빼면 왼쪽으로 이동함

 

미분값을 뺐더니 함숫값이 감소하면서 극솟값을 찾고 있음

 

극값에서는 f’(x)=0이므로 더하고 빼도 점이 더 이상 이동하지 못하면서 이럴 때 목적함수가 최적화된 상태라고 말한다