softmax function에 대한 진정한 의미

1. 선형모형

 

$O=XW+b$의 형태, $X$는 input, $W$는 가중치(Weight), $b$는 절편(intercept), $O$는 선형모형에 들어간 $X$의 Output

 

그림1. 선형모형의 수학적 형태

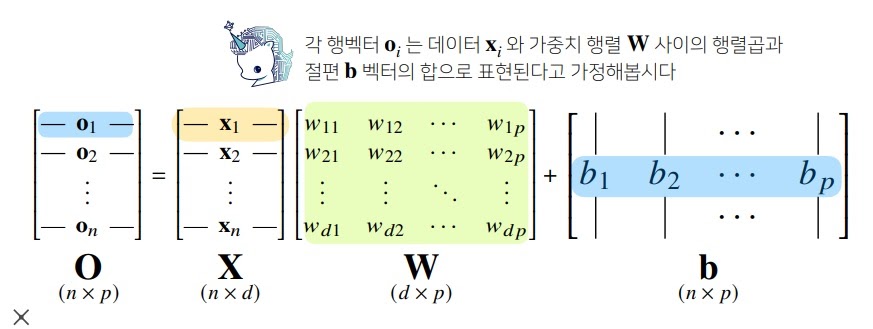
그림1을 보면 데이터 $X$가 n*d차원에서 선형모형을 통과하면서 n*p차원의 $O$로 바뀜

 

d개의 input 변수가 가중치의 조합에 의해 p개의 선형 output 변수로 바뀌는 모형

 

그림2. 선형모형 mapping 그림

 

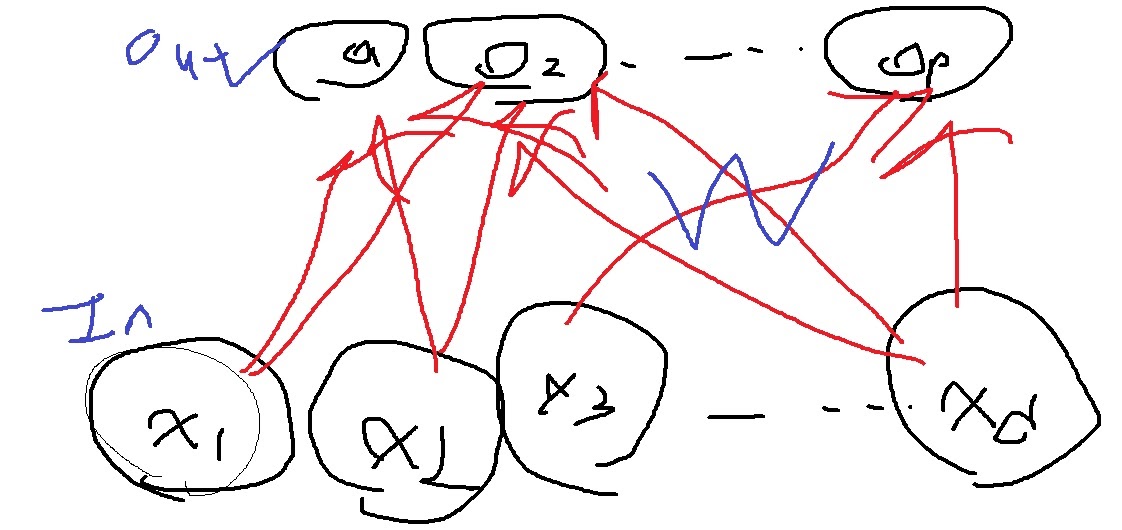
d개의 변수가 가중치에 의한 선형결합으로 각각의 output변수 $O_{1}$,$O_{2}$,...,$O_{p}$가 나옴

 

 

2. softmax

 

input 값을 각 class에 속할 확률벡터로 변환해주는 활성화함수

 

\[softmax(O) = (\frac{exp(O_{1})}{\sum_{k=1}^{p} exp(O_{k})}, \frac{exp(O_{2})}{\sum_{k=1}^{p} exp(O_{k})},..., \frac{exp(O_{p})}{\sum_{k=1}^{p} exp(O_{k})})\]

 

softmax함수는 선형모델의 출력값을 확률로 변환하여 해석할 수 있게 해준다.

 

$$softmax(O)=softmax(WX+b)$$

 

그림3. softmax function 코드로 구현

 

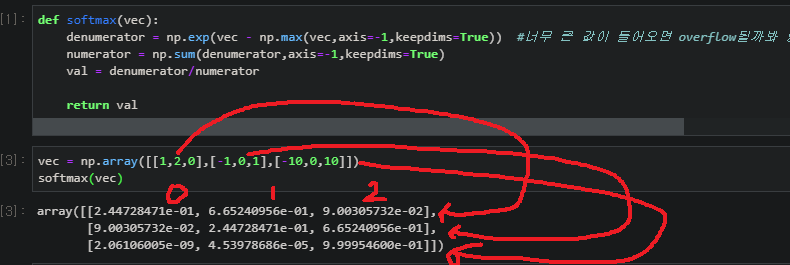
input값이 어디에 속할지 마지막 추론할때는

 

one hot encoding으로 가장 확률이 높은 class의 주소만 1로하고 나머지는 0으로한 벡터를 결과로 출력

 

그림4. softmax를 이용한 추론 코드 구현

 

근데 나는 이 그림을보고 의문이 들어서 고민을 하다가 엄청난 결론을 내려버렸다

 

선형모형으로 뱉은 O를 softmax로 확률로 바꾼 뒤에

 

거기서 가장 확률이 높은 class에 one hot encoding으로 1로 바꾼다로 알고 있었는데

 

그냥  O에서만 바로 최댓값을 1로 바꾸는 one hot encoding을 해버리니까 의문이 든거임 왜?

 

 

3. softmax classification

 

근본적으로 (신경망을 이용한) classification은 선형모형으로 예측할려고 한거임

 

애초에 비선형모형이라는 생각을 버려야한다는것

 

input이 주어질 때 각 class에 속할 조건부 확률을 선형모형으로 예측하고싶은 것

 

예를 들어서 4개의 input 변수로 3개의 class를 예측하는 모형을 만들고자 할 때 이런 선형모형을 생각한거임

 

그림5. classification에 대한 근원적인 모형

 

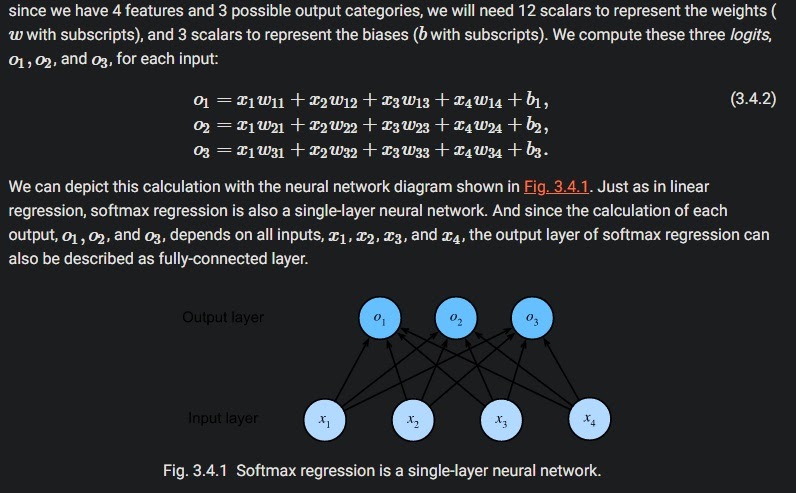
그런데 이 모형에서 나온 결과값 O를 확률로 예측하자니 문제가 생긴것.

 

왜냐하면 결과값의 합이 1이되는 것도 아니고, 음수가 될 수도 있는 것

 

수학자들은 이러한 결과를 확률로 해석하기 위해 softmax 함수를 도입하는 것임

 

그림6. softmax에 대한 정의

 

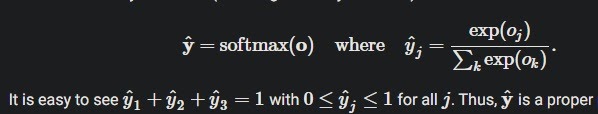
근데 사실 softmax로 바꾼 값을 one hot encoding해도 되긴한데

 

결과값 O를 바로 one hot encoding해야하는 이유는 컴퓨터 연산이 효율적이기 때문이겠지

 

그리고 수학적으로도 softmax함수가 증가함수여서

 

O의 증감을 바꾸지 않기 때문에 softmax로 바꾼 확률의 최댓값이 있는 주소는 O에서 최댓값이 있는 주소와 동일함

 

그렇기 때문에 softmax로 바꾸기 전 선형 결과값 O도 사실상 class에 속할 가능성(likelihood?)을 측정해주는거임

 

softmax가 사실상 비선형함수이지만 이런 이유때문에 softmax classification은 근본적으로는 선형모형이다

 

 

그림7. softmax regression에 대한 근본적인 설명

 

4. 참고

 

https://d2l.ai/chapter_linear-networks/softmax-regression.html