1. 선형회귀분석
주어진 n개의 데이터에서 이들을 가장 잘 설명하는 선형모형을 찾는다
이전에는 무어펜로즈 역행렬을 이용하여 찾았다

무어펜로즈 역행렬을 이용하여 오차의 norm을 최소화하여 회귀계수 $\beta$를 찾는다.
무어펜로즈 역행렬은 컴퓨터 계산 시간 측면에서 비효율적이다
변수 수 m에 따라 $O(m^{2})$이라고 한다.
대안으로 경사하강법을 이용하여 회귀계수를 추정할 수 있다.
2. 선형회귀분석에서의 경사하강법
선형회귀분석은 위에서도 보였지만 \[y-X\beta\]의 norm을 최소화하는 $\beta$를 찾는것.
그러므로 \[y-X\beta\]의 norm을 $\beta$로 미분한 그래디언트 벡터를 구한다

그래디언트 벡터를 구하면 경사하강법을 이용하여 $\beta$에 그래디언트 벡터를 빼서 얻은 값을 새로운 $\beta$로 갱신한다
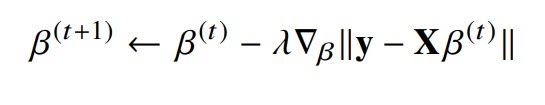
참고로 \[y-X\beta\]의 norm의 제곱을 최소화시키는 최소제곱법이 계산에서 더 간단하다

3. 경사하강법 코드 구현
import numpy as np
X=np.array([[1,1],[1,2],[2,2],[2,3]])
y= np.dot(X,np.array([1,2]))*3
beta_gd = [10.1,15.1,6.5]
X_ = np.array([np.append(x,[1]) for x in X]) #절편항을 추가함
for t in range(5000):
error = y-X_@beta_gd
error = error/(np.linalg.norm(error))
grad = np.transpose(X_)@error
beta_gd = beta_gd-0.01*grad
print(beta_gd)
[1.01556612 2.02103742 3.009597]
종료조건이 그래디언트 벡터의 크기가 0이 되는 것이 아니라 반복횟수라는 것도 중요함
이것이 요즘 대세라는데?
학습횟수는 너무 작으면 목표값에 수렴하지 않게된다
학습률은 너무 작으면 수렴이 너무 느려지고
또 너무 크면 수렴을 못하고 overshooting이 일어날수도 있다
import numpy as np
X=np.array([[1,1],[1,2],[2,2],[2,3]])
y = np.dot(X,np.array([1,2]))*3
beta_gd = [10.1,15.1,6.5] #초기값
X_ = np.array([np.append(x,[1]) for x in X])
for t in range(100):
error = y-X_@beta_gd
error = error/(np.linalg.norm(error))
grad = np.transpose(X_)@error
beta_gd = beta_gd-0.05*grad
print(beta_gd)
[3.52272924 5.43014629 -8.61096994]학습횟수와 학습률이 경사하강법에서 중요하게 생각해야할 hyperparameter로 결과가 달라진다
이전 학습횟수 5000, 학습률 0.01과 바로 위 학습횟수 100, 학습률 0.05의 결과가 조금 다르다.
실제 정답은 [1,2,3]이라고 함
4. 경사하강법의 한계
전구간에서 미분가능이고 아래로 볼록(convex)일 때 적절한 학습률과 학습횟수를 선택하면 최솟값을 찾는다.
선형회귀문제는 \[y-X\beta\]의 norm이 $\beta$에 대해 아래로 볼록이라 쉽지만
일반적으로 다루는 비선형문제에서는 경사하강법이 수렴을 보장하지 않는다
또 데이터 세트가 매우 크면 수렴 속도가 매우 느리다

5. 참고
https://songminkee.github.io/studyblog/hands%20on%20machine%20learning/2020/05/15/4.html
4. 모델훈련 · Monch
15 May 2020 • Hands On Machine Learning 선형 회귀 일반적으로 선형 모델은 입력 특성의 가중치(weight) 합과 편향(bias)이라는 상수를 더해 예측을 만든다. \(\hat{y}=\theta_{0}+\theta_{1}x_{1}+\theta_{2}x_{2}+...+\theta_{
songminkee.github.io
'딥러닝 > 딥러닝 기초' 카테고리의 다른 글
| 확률적 경사하강법(stochastic gradient descent method) (0) | 2022.01.04 |
|---|---|
| cross validation이란? (0) | 2022.01.03 |
| 여러가지 optimizer의 원리 (0) | 2022.01.02 |
| 신경망은 무엇이고 딥러닝에서 활성화함수를 왜 사용하는가? (0) | 2021.12.31 |
| 여러가지 활성화함수(activation function) (0) | 2021.12.31 |

