확률적 경사하강법(stochastic gradient descent method)
1. 확률적 경사하강법(stochastic gradient descent method, SGD)
모든 데이터를 사용하는 것이 아닌 매 스텝마다 데이터 1개를 sampling하여 각 스텝마다 gradient를 계산한 경사하강법
목적식이 볼록(convex)이 아니면 확률적 경사하강법을 이용하여 최적화 할 수 있다.
또한 데이터 세트가 매우 클때 일반적인 경사하강법은 속도가 너무 느려져서
매 스텝마다 일부 데이터만 사용하는 확률적 경사하강법을 이용하여 속도를 높일 수 있다.
연산량에 있어서 효율적임
만능은 아니지만 딥러닝에서는 일반적인 경사하강법보다 낫다고한다
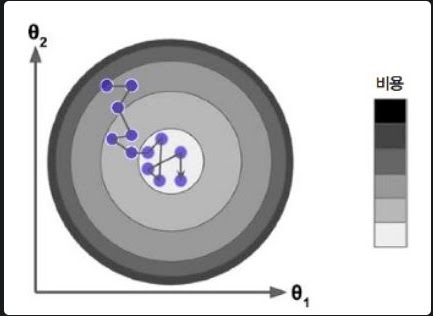
그림1을 보면 데이터의 일부를 사용하여 추정한 그래디언트 벡터의 기댓값이 실제 그래디언트 벡터에 근사한다
데이터를 확률적으로 선택하기 때문에 안정적으로 global minimum으로 접근하지 않고 요동치면서 접근한다
시간이 지나면 최솟값에 접근하나 요동치기 때문에 알고리즘이 멈춘다고 해서 최적값이라는 보장은 없다
cost function이 복잡할 수록 요동치면서
local minimum을 피할 수 있게 해주면서 global minimum으로 접근할 확률을 높이지만
요동치기때문에 안정적으로 global minimum에 안착하지 못한다는 점이 단점이다
학습률을 점진적으로 감소(학습 스케줄링)시켜서 최적으로 선택해야한다는데 어렵다
2. 미니배치 경사하강법(mini batch gradient descent)
데이터의 일부를 sampling하여 이것으로 gradient를 계산하는 경사하강법
확률적 경사하강법(SGD)보다 덜 불규칙하며
global minimum에 더욱 안착할 수 있지만 local minimum을 못 피할 확률이 커진다
경사하강법(Batch)이 매우 느리지만 확실하게 접근하는 것을 보여주고
확률적 경사하강법(stochastic), 미니 배치 경사하강법(mini-batch)은 빠르지만 불안정하다
3. 확률적 경사하강법은 왜 가능한가
일반적인 batch 경사하강법은 전체 데이터 세트를 이용하여 목적함수의 그래디언트 벡터를 계산한다
확률적 경사하강법은 일부 데이터 셋을 이용하여 목적함수의 그래디언트 벡터를 계산한다
일부 데이터 셋을 이용하기 때문에 목적함수가 약간 달라질 수 있다
왜냐하면 함수는 데이터를 집어넣은 함숫값들의 모임이면서 그 값들을 찍어내면서 함수 그래프를 그리거든
sampling을 여러번하여 매번 다른 미니배치를 사용하여
매번 목적함수가 달라지면서 일반적인 경사하강법과는 다른 그래디언트 벡터가 나오겠지만
그래도 근사적으로 최솟값으로 비슷하게 갈 것이라고 기대할 수가 있다
일부 데이터 셋을 사용하기때문에 매 스텝마다 빠르게 계산하지만 요동치면서 불안정하게 접근한다는 점이 단점이다
아무튼 데이터가 큰 요즘 시대에 매우 효율적이다
근데 그게 정답이냐는 다른 문제잖아
4. 참고
https://songminkee.github.io/studyblog/hands%20on%20machine%20learning/2020/05/15/4.html
4. 모델훈련 · Monch
15 May 2020 • Hands On Machine Learning 선형 회귀 일반적으로 선형 모델은 입력 특성의 가중치(weight) 합과 편향(bias)이라는 상수를 더해 예측을 만든다. \(\hat{y}=\theta_{0}+\theta_{1}x_{1}+\theta_{2}x_{2}+...+\theta_{
songminkee.github.io
'딥러닝 > 딥러닝 기초' 카테고리의 다른 글
| backpropagation의 개괄적인 설명 (0) | 2022.01.26 |
|---|---|
| 여러가지 cross validation 방법들 (0) | 2022.01.17 |
| cross validation이란? (0) | 2022.01.03 |
| 경사하강법(gradient descent)의 한계 (0) | 2022.01.02 |
| 여러가지 optimizer의 원리 (0) | 2022.01.02 |
