1. 강한 연결 요소(strongly connected component)
방향그래프에서 임의의 정점 v1,v2를 골랐을때, 항상 v1과 v2를 서로 오갈 수 있는 경로가 존재한다면,
그러한 방향 그래프를 강한 연결 요소(SCC)라고 부른다.
이 정의에 의하면 무방향 그래프에서는 전체 그래프가 반드시 강한 연결 요소가 되므로 의미가 없다.
즉, 방향 그래프에서만 의미있는 정의가 된다.
아무튼 예를 들어 다음 그래프는 모든 정점 쌍 (v1,v2)에 대하여 서로 오가는 경로가 존재하는 강한 연결 요소이다.

하지만 다음 그래프는.. 2번에서 5번으로는 갈 수 있어도 5번에서 2번으로 올 수는 없다.
그러므로 강한 연결 요소가 아니다.
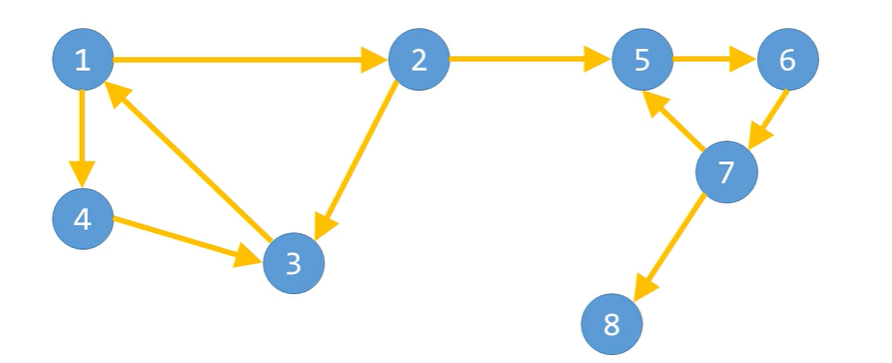
하지만 그래프를 다음과 같이 적당히 분할하면, 분할된 그룹들 [1,2,3,4], [5,6,7], [8]은 강한 연결 요소들이 된다.

결국에 관심있는건 주어진 방향 그래프의 일부 정점들을 가장 크게 묶어서 여러개의 강한 연결 요소들로 분할 할 수 있는가?이다.
2. 코사라주 알고리즘(kosaraju's algorithm)
2번의 DFS로 전체 그래프에서 SCC를 모두 구하는 알고리즘
O(V+E)의 빠른 시간 복잡도에 구현이 매우 쉽다는 장점이 있다.
2-1) 첫번째 DFS
1) 번호 num = 1을 global로 설정
2) 그래프의 모든 정점을 순회해서 아직 방문하지 않은 점 V가 존재한다면, 해당 V에서 DFS 수행
3) DFS를 수행하는 중에, 더 이상 방문할 정점이 없다면 마지막으로 방문된 정점에 num값을 저장
4) num 값을 1 증가
5) 모든 정점이 방문체크 될때까지 위 과정을 반복
--------------------------------------------------------------------------------------------------------------------------------------------
num = 1로 시작
1번~8번을 차례대로 방문을 수행하는데 1번이 방문체크 되어 있지 않으니 1번부터 방문 시작

DFS 수행중 8번으로 이동하면, 8번을 방문 체크 하고 다음으로 가는데...
8번에서는 더 이상 갈 수 없으므로 8번에 num = 1을 기록하고.. num을 1 증가

다시 1번에서 5번 > 6번으로 진행을 하다가.. 더 이상 이동할 수 없으므로
6번에 num = 2를 기록하고 num값을 1 증가
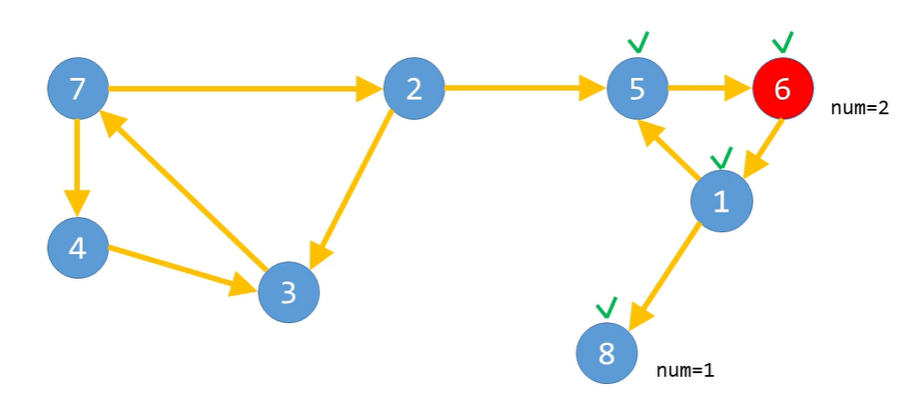
이제 모든 경우에서 더 이상 진행할 수가 없다.
6번에서 return되면서 5번, 1번으로 차례대로 돌아오는데.. 돌아올때마다 더 이상 이동이 불가능하므로
5번 정점에는 num = 3을 기록하고 num 1 증가
1번 정점에는 num = 4를 기록하고 num 1 증가

DFS가 끝났은니, 1번~8번중 아직 방문되지 않은 정점을 찾는다.
2번이 아직 방문되지 않았으니 2번부터 DFS 시작
현재 num = 5이다.

2번부터 시작해서, 3번, 7번, 4번으로 이동하고 더 이상 이동 불가능하므로 4번에 num = 5를 기록하고 1 증가
모든 곳이 이동 불가능하므로 7번, 3번, 2번으로 되돌아가면서 num =6, num = 7, num = 8을 기록한다.

2-2) 두번째 DFS
1) 모든 방문 기록을 초기화한다.
2) 주어진 그래프의 간선을 모두 반전시킨다.
3) 기록된 num값의 내림차순으로 정점들을 선택한다.
4) 선택된 정점이 방문된 적이 없다면, 이를 시작점으로 DFS를 수행
5) DFS 과정에서 방문된 점들이 모두 하나의 강한 연결 요소가 된다.
------------------------------------------------------------------------------------------------------------------------------------------------
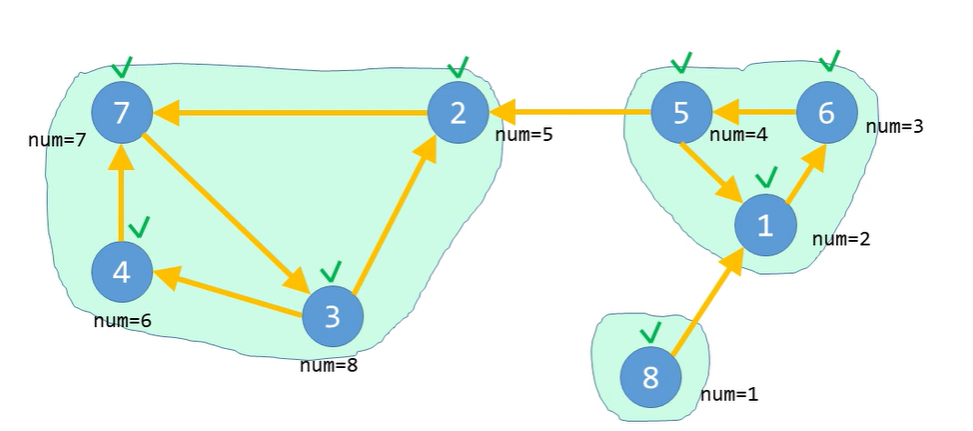
다음과 같이 모든 간선을 반전시키고 num을 내림차순으로 확인해서..
가장 큰 값이 기록된 2번 정점부터 DFS를 시작

그러면 2번, 7번, 3번, 4번을 차례대로 방문하면서.. 이들이 하나의 강한 연결 요소가 된다.

다음으로 num의 내림차순으로 3,7,4를 차례대로 확인하는데 각각 방문되어 있으므로.. 넘어가고
1번 정점은 방문되지 않았으니 여기서 DFS를 시작

그러면 1번 6번 5번을 차례대로 방문하면서 하나의 SCC를 만든다
또한 그 다음으로 8번은 자체적으로 더 이상 방문할 곳이 없으니 하나의 SCC가 된다.
예상한대로 모든 SCC를 정확하게 구하였다.
3. 알고리즘에 대한 분석
SCC란 정의에 의해 임의의 정점 v1,v2를 골랐을때 v1과 v2를 서로 오가는 경로가 존재한다.
따라서 사이클을 이루기 때문에 간선을 반전시켜도 여전히 SCC가 된다.

첫번째 DFS를 수행할때 구한 num의 의미에 대해 생각해본다면..
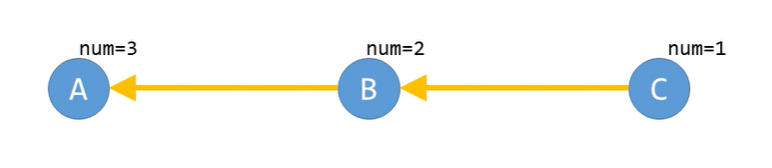
마지막으로 방문한 정점에 num값을 기록하므로 다음과 같은 단순한 경로에서는 어떠한 정점에서 시작하더라도
다음과 같이 num값이 동일하다.
또한 마지막에 더 이상 방문이 불가능하면 num을 기록하므로 결국 num값이 큰쪽에서 작은쪽으로 이동하게 된다.

두번째 DFS에서는 이 그래프를 반전시키고 num값이 큰쪽에서 DFS를 수행하게 된다.
이 때 큰 번호에서 DFS를 수행하여 아직 방문하지 않은 정점을 이동하는데, 그럴 수 있다면 그 정점의 번호는
현재 출발점의 번호보다 더 작다.
왜냐하면 애초에 num값이 큰 순서대로 정점을 선택하여 DFS를 수행했기 때문에, 아직 방문하지 않은 정점은..
무조건 출발점보다 작아야한다.
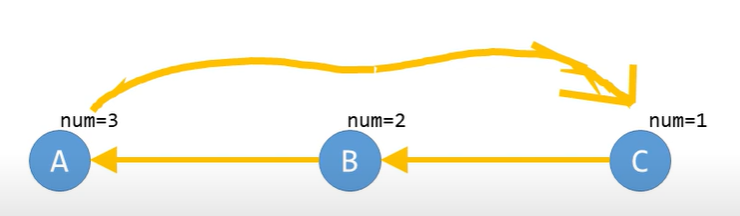
만약 뒤집은 그래프에서 큰 번호에서 작은 번호로 이동하는 경로가 존재한다면,
뒤집지 않은 원본 그래프에서도 큰 번호에서 작은 번호로 이동하는 경로가 존재하기 때문에 해당 그래프는 사이클을 이룬다.
사이클을 이루는 순간 SCC를 만족하므로 두번째 DFS까지 수행하면 모든 SCC를 찾을 수 있게 된다.
4. 연습문제
2150번: Strongly Connected Component (acmicpc.net)
2150번: Strongly Connected Component
첫째 줄에 두 정수 V(1 ≤ V ≤ 10,000), E(1 ≤ E ≤ 100,000)가 주어진다. 이는 그래프가 V개의 정점과 E개의 간선으로 이루어져 있다는 의미이다. 다음 E개의 줄에는 간선에 대한 정보를 나타내는 두 정
www.acmicpc.net
5. 풀이
위 알고리즘 그대로 구현하면 된다
DFS 모두 비재귀로 구현해볼려 했는데, 첫번째 DFS가 비재귀로 구현하기 까다롭다..
마지막에 방문된 정점에서 더 이상 이동 불가능하면 num을 기록할려고 했는데...
그 이후에 더 이상 이동 불가능할경우, 이미 방문된 정점들에도 num값을 기록해줘야하는데
이게 좀 까다롭더라고.. 억지로 하자니 매우 느려질것 같고..
그래서 첫번째는 재귀 dfs로 하고 두번째는 비재귀 dfs로 만들었다
-----------------------------------------------------------------------------------------------------------------------------------------------
또한 나름의 디테일 중 하나는 num_list = [0]*(v+1)에서 index가 num값이고 value가 정점 번호이다.
이러면 두번째 dfs에서 num_list를 정렬할 필요 없이 그냥 index의 마지막부터 순회하면
num값이 가장 큰 정점 num_list[i]로 바로 찾을 수 있다.
-------------------------------------------------------------------------------------------------------------------------------------------
또한 처음에 그래프를 구성할때, 여기서 반전된 그래프도 만들어둔다.
두번째 dfs할때 만들려고 하면 비효율적이니까.
#find strongly connected component
#kosaraju's algorithm
from sys import stdin,setrecursionlimit
setrecursionlimit(10**6)
#첫번째 DFS
def dfs1(s,graph,visited):
global num
for u in graph[s]:
#아직 방문하지 않은 정점이면, 방문 체크를 하고 다음 정점으로 이동
#주의!
#한번의 visitied로 해결해야하기 때문에, dfs1 끝나고 나서 visited[u] = 0으로 하면 안된다.
if visited[u] == 0:
visited[u] = 1
dfs1(u,graph,visited)
#s에서 더 이상 이동할 수 없는 경우
#현재 num값을 s에 기록한다.
#중요한 점은 num_list[num] = s로 기록해야한다.
#두번째 DFS에서 num값이 큰 정점부터 시작해야하는데, num_list[s] = num으로 하면 정렬해야하지만
#num_list[num] = s로 한다면 index의 역순으로 순회하기만 하면 되니까 간단해짐
num_list[num] = s
num += 1
#두번째 DFS
def dfs2(s,visited,graph):
stack = [s]
scc = []
while stack:
u = stack.pop()
if visited[u] == 1:
continue
visited[u] = 1
scc.append(u) #s부터 시작해서 방문하는 정점 u마다 SCC를 이루므로 append해준다.
for w in graph[u]:
if visited[w] == 0:
stack.append(w)
return scc,visited #한번의 visited로 해결해야하므로, 재활용해야함
#kosaraju algorithm
def kosaraju(v,graph,reverse):
#첫번째 DFS
#num_list를 만든다.
visited = [0]*(v+1)
for i in range(1,v+1):
if visited[i] == 0:
visited[i] = 1
dfs1(i,graph,visited)
#두번째 DFS
#모든 SCC를 찾는다.
visited = [0]*(v+1)
scc_list = []
#num_list의 index의 역순으로 순회하면 num_list[i]는 num값이 큰 정점 번호를 나타낸다.
for i in range(v,0,-1):
if visited[num_list[i]] == 0:
scc,visited = dfs2(num_list[i],visited,reverse) #주의: 반전된 그래프를 사용해야한다.
scc.sort() #문제에서 오름차순으로 정렬해서 출력하라했으므로,
scc_list.append(scc)
return scc_list
v,e = map(int,stdin.readline().split())
graph = [[] for _ in range(v+1)]
reverse = [[] for _ in range(v+1)]
for _ in range(e):
x,y = map(int,stdin.readline().split())
graph[x].append(y)
reverse[y].append(x) #두번째 dfs에 필요하므로 반전된 그래프를 미리 만든다
num = 1
num_list = [0]*(v+1)
scc_list = kosaraju(v,graph,reverse)
scc_list.sort() #문제에서 오름차순으로 출력하라고 해서
print(len(scc_list))
for scc in scc_list:
scc.append(-1)
print(' '.join(map(str,scc)))
속도가 0.2초로 다른 코드랑 비교해서 괜찮은거 보면 나름 구현 잘한듯..?
https://www.youtube.com/watch?v=iKNkpiQhsE0
'알고리즘 > 그래프 이론 정복기' 카테고리의 다른 글
| DFS 2번으로 트리의 지름을 구하는 방법 (0) | 2023.11.28 |
|---|---|
| 저울의 무게 비교를 그래프로 바꿔서 최단 거리 알고리즘으로 해결(플로이드 워셜, 그래프 탐색) (0) | 2023.09.07 |
| Binary Lifting을 이용한 개선된 최소 공통 조상(Lowest Common Ancestor) 구하는 방법 배우기2 (0) | 2023.08.13 |
| 최소 공통 조상(Lowest Common Ancestor,LCA)문제 기본 해법 배우기1 (0) | 2023.08.07 |
| 컴퓨터로 한붓그리기 하는 방법 - 오일러 경로를 찾는 알고리즘 (0) | 2023.02.19 |

