1. 문제
16168번: 퍼레이드
첫 번째 줄에 지점의 개수 V, 연결 구간의 개수 E가 주어진다. (1 ≤ V ≤ E ≤ 3000) 이후 E개의 줄에 걸쳐 각 연결 구간이 연결하는 두 지점의 번호 Va, Vb가 공백을 사이에 두고 주어진다. (1 ≤ Va,
www.acmicpc.net
2. 오일러 경로(eulerian trail)
"모든 변을 단 한번만 지나서 주어진 그래프를 완성할 수 있는가"

그래프의 모든 간선을 1번만 지나서 모든 정점을 방문하는 연속된 경로를 오일러 경로라고 부른다
혹은 한붓그리기라고도 불린다.
위와 같이 정점은 여러번 지나도 상관없다
위와 같은 그래프는 오일러 경로가 존재하는 그래프이다.
특히 시작점과 끝점이 같은 오일러 경로는 오일러 회로(eulerian circuit)라고 부른다
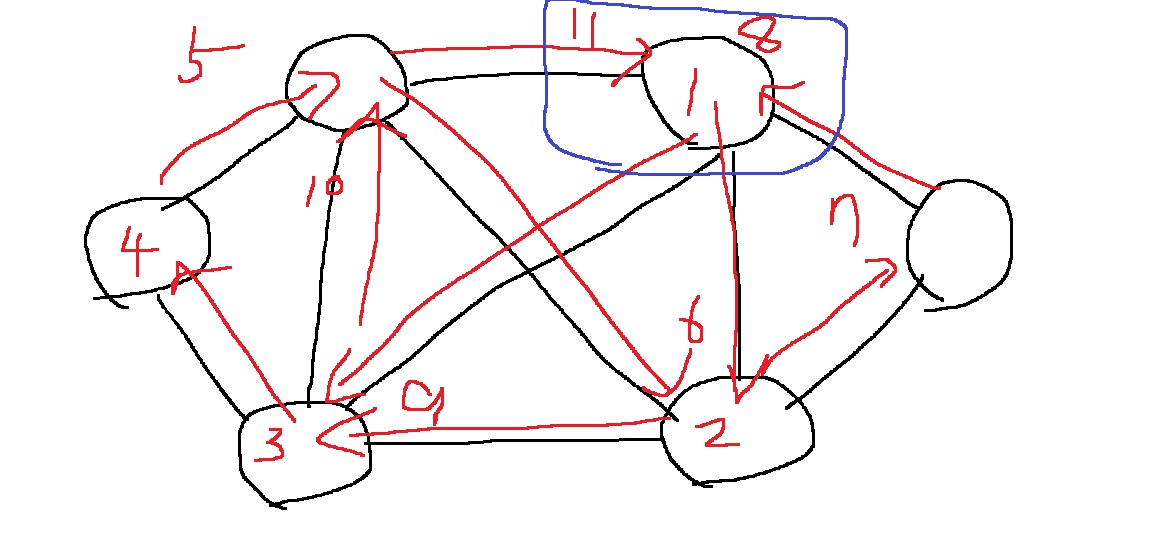
주의할 점은 모든 지점을 지나지는 않아도 된다는 점이다
모든 간선만 한번씩 지나는 경로라면 그것은 오일러 경로다
그래서 다음과 같은 경우도 오일러 경로가 존재하는 그래프다.
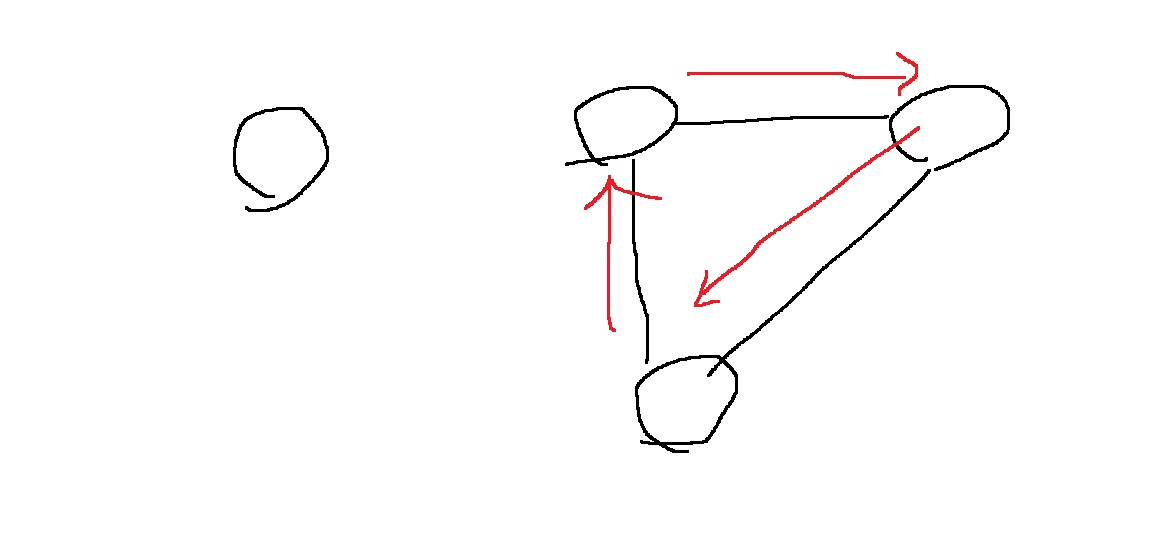
3. 오일러 경로가 존재할 필요충분조건
방향이 없는 그래프와 방향이 있는 그래프에 따라 다르다
3-1) 방향이 없는 그래프에서 오일러 회로
방향이 없는 그래프에서 오일러 회로(시작 정점과 끝 정점이 같다)가 존재할 필요충분조건은 모든 정점의 차수가 짝수이다.
간단하게 생각해본다면,
시작점과 끝점이 동일한데, 그러한 점의 나가는 간선과 들어오는 간선의 개수가 서로 같아야한다.
들어오는 간선이 1개 있고 나가는 간선이 없다면... 들어오는 순간 나갈 수가 없으니까 그래프의 다른 간선은 지나갈 수가 없다
그러므로 이는 모든 다른 정점에도 동일하게 적용된다.
그래서 오일러 회로가 존재할 필요충분조건은 모든 정점의 차수가 짝수인 경우이다.
3-2) 방향이 없는 그래프에서 오일러 경로
모든 정점이 짝수 차수를 가진다면 오일러 회로(는 오일러 경로이기도 하다)를 가지며,
오직 2개의 정점이 홀수 차수를 가진다면 오일러 경로를 가진다.
특히 그러한 2개의 정점은 각각 시작점과 끝점이 된다.
간단하게 생각해본다면 시작점과 끝점은 나가고 나서 다시 들어오지 않아도 되기 때문에 두 지점은 홀수 차수를 가지면 된다
다음은 두 정점이 홀수차수니까 오일러 경로가 존재할 것이다.
그리고 그 두 정점은 시작 정점과 끝 정점이 될 것이다.
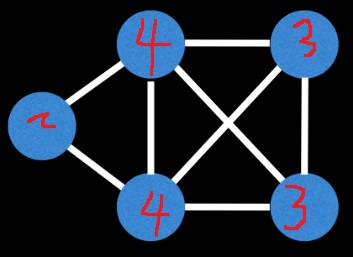
다음은 오일러 경로

3-3) 방향이 있는 그래프에서 오일러 회로
방향이 있는 그래프는 들어오는 차수와 나가는 차수가 있다.
오일러 회로는 모든 정점이 들어오는 만큼 나가는 간선도 존재해야하므로,
방향이 있는 그래프에서 오일러 회로가 존재할 필요충분조건은 모든 정점이 들어오는 차수와 나가는 차수가 동일한 것이다.
3-4) 방향이 있는 그래프에서 오일러 경로
최대 1개의 정점이 (들어오는 차수 - 나가는 차수 = 1) = 끝 정점이고, 최대 1개의 정점이 (나가는 차수 - 들어오는 차수 = 1) = 시작 정점이며
나머지 모든 정점은 들어오는 차수와 나가는 차수가 동일한 것이다
오일러 경로는 시작 정점과 끝 정점이 서로 다른 경우도 포함한다.
따라서, 시작 정점은 나가는 차수가 들어오는 차수보다 1 크면 된다. 결국 다시 안들어오면 되니까 나가는 경우가 하나 더 많으면 된다.
마찬가지로 끝 정점은 들어오는 차수가 나가는 차수보다 1 크면 된다. 다시 안나가면 되니까 들어오는 경우가 하나 더 많으면 된다.

위와 같은 경우는 모든 정점이 들어오는 차수와 나가는 차수가 동일하므로 오일러 회로가 존재할 것이다.
다음은 오일러 회로
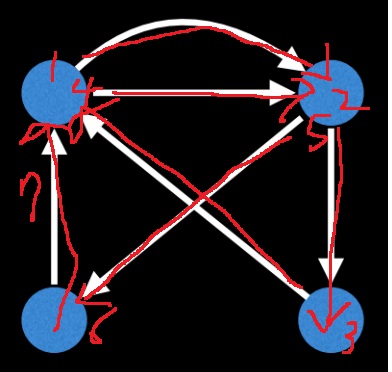
4. 풀이
문제의 핵심은 "모든 지점을 지나면서 모든 연결 구간들을 1번만 지나는 경우가 존재하냐 아니냐를 판단하는 것이다"
기본적으로 오일러 경로와 회로는 모든 지점을 지나지 않아도 되지만 이 문제는 모든 지점을 지나는 경우를 요구하고 있다
따라서 union find를 통해 간선이 주어질때마다 union을 시킨다.
union이 끝나고 모든 점이 하나의 집합을 이루는지 판단한다.
하나의 집합을 이룬다면, 각 정점의 차수를 세서 정점의 차수가 모두 짝수개인지, 혹은 두 정점만 홀수개인지를 판단한다.
그렇다면 문제에서 요구하는 오일러 경로나 오일러 회로가 존재하게 된다.
from sys import stdin
def find_parent(x,parent):
if x != parent[x]:
parent[x] = find_parent(parent[x],parent)
return parent[x]
def union(a,b,parent):
a = find_parent(a,parent)
b = find_parent(b,parent)
if parent[a] < parent[b]:
parent[parent[a]] = parent[b]
else:
parent[parent[b]] = parent[a]
v,e = map(int,stdin.readline().split())
graph = [[] for _ in range(v+1)]
parent = [i for i in range(v+1)]
answer = True
#모든 간선을 union시킨다.
for _ in range(e):
a,b = map(int,stdin.readline().split())
graph[a].append(b)
graph[b].append(a)
if find_parent(a,parent) != find_parent(b,parent):
union(a,b,parent)
#모든 점의 집합이 하나의 집합을 이루는지 판단한다
one = set()
for i in range(1,v+1):
one.add(find_parent(i,parent))
#하나의 집합을 이룬다면...
if len(one) == 1:
odd = 0
#홀수차수 정점이 2개이거나 0개인지 판단한다.
for row in graph:
if len(row) % 2 == 1:
odd += 1
if odd == 2 or odd == 0:
print("YES")
else:
print("NO")
#하나의 집합을 이루지 못한다면...
else:
print("NO")
[Algorithm] 오일러 경로 (tistory.com)
'알고리즘 > 그래프 이론 정복기' 카테고리의 다른 글
| Binary Lifting을 이용한 개선된 최소 공통 조상(Lowest Common Ancestor) 구하는 방법 배우기2 (0) | 2023.08.13 |
|---|---|
| 최소 공통 조상(Lowest Common Ancestor,LCA)문제 기본 해법 배우기1 (0) | 2023.08.07 |
| 최대힙, 최소힙 직접 구현하기 (0) | 2022.10.02 |
| 트리 응용 알고리즘 몇가지 - 자손, 루트, 조상찾기, 서브트리 부분순회 - (0) | 2022.09.30 |
| 그래프 이론 - 서로소집합(disjoint set) 기본개념1 - (0) | 2022.09.29 |

