https://www.youtube.com/watch?v=O895NbxirM8&list=PLRx0vPvlEmdAghTr5mXQxGpHjWqSz0dgC&index=15
LCA(Lowest Common Ancestor) 알고리즘
LCA(Lowest Common Ancestor) 알고리즘이란? LCA 알고리즘이란 영어 해석 그대로 최소 공통 조상을 찾는 알고리즘이고, 두 정점 u, v(혹은 a, b)에서 가장 가까운 공통 조상을 찾는 과정을 말한다. 예를들어
www.crocus.co.kr
https://kibbomi.tistory.com/201
최소 공통 조상 (LCA, Lowest Common Ancestor)(C/C++)
여러 자료를 참조하면서 LCA를 공부했는데, 어떤 자료는 너무 쉽고 깔끔하지 못하고, 어떤 자료는 난이도가 있고 깔끔하게 설명된 자료였습니다. 그래서 여러 자료를 찾아보며 이해하고, 또 이해
kibbomi.tistory.com
https://en.wikipedia.org/wiki/Lowest_common_ancestor
Lowest common ancestor - Wikipedia
From Wikipedia, the free encyclopedia In computer science, lowest (i.e. deepest) node that has both v and w as descendants In this tree, the lowest common ancestor of the nodes x and y is marked in dark green. Other common ancestors are shown in light gree
en.wikipedia.org
1. 최소 공통 조상(LCA)
In graph theory and computer science, the lowest common ancestor (LCA) (also called least common ancestor) of two nodes v and w in a tree or directed acyclic graph (DAG) T is the lowest (i.e. deepest) node that has both v and w as descendants, where we define each node to be a descendant of itself (so if v has a direct connection from w, w is the lowest common ancestor).
트리(tree)나 DAG에서 두 정점 u,v에 가장 가까운 공통 조상
DAG는 방향이 있고 사이클이 없는 그래프를 말한다.
여기서 u가 v의 자식이라면, v가 최소 공통 조상이 될 수 있다.
즉 다음과 같은 경우, 6과 13의 최소 공통 조상은 13이다.
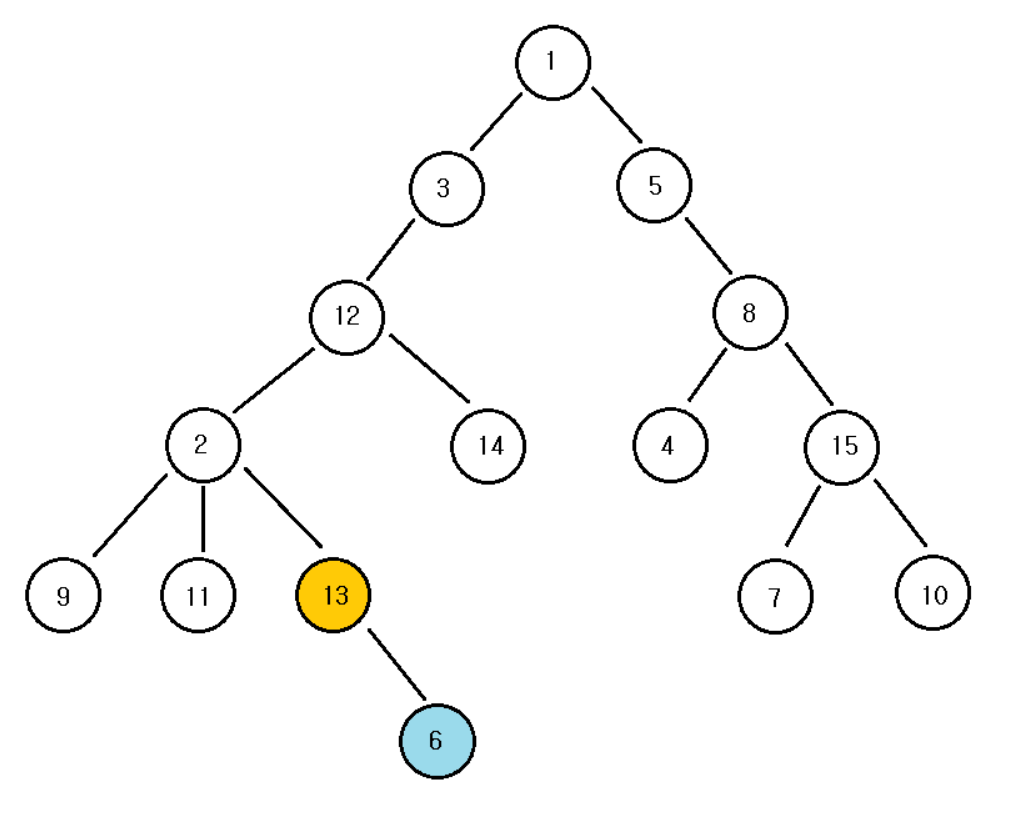
예를 들어 다음 그래프에서.. 8번 노드와 15번 노드를 보면..

가장 가까운 공통 조상은 2번 노드이다.
"가장 가까운"이라는 말은 "트리의 깊이(depth)가 가장 낮은(lowest)"이라는 말과 같다.
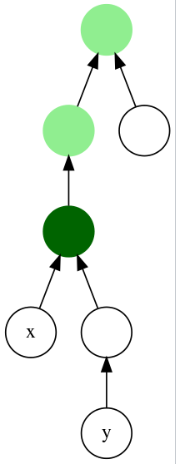
위 그래프에서 x,y 노드의 조상은 초록색으로 표시된 노드들이지만, 최소 공통 조상은 가장 짙은 초록색으로 표시된 노드이다.
2. 기본 알고리즘
가장 단순하게 생각하면, 두 노드 u,v에서 포인터를 두고, 차례대로 한단계씩 부모로 만날때까지 거슬러 올라가면서, 확인해보는 방법이 있다.
이는 노드 수가 N개일때, 최악의 경우 모든 노드 N개를 검사해보는 O(N) 선형탐색 방법이다.
1) 먼저 DFS를 이용해 트리의 모든 노드의 깊이(depth)를 계산해준다.
루트 노드에서 각 노드로의 거리가 깊이와 동일

2) 예를 들어, 8번 노드와 15번 노드의 최소 공통 조상을 찾고 싶다면,
먼저 두 노드의 깊이가 동일하도록 맞춰준다
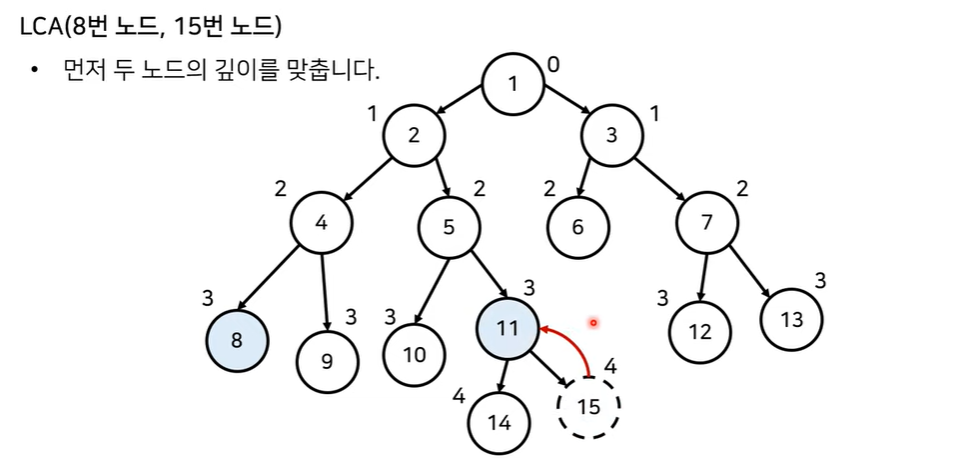
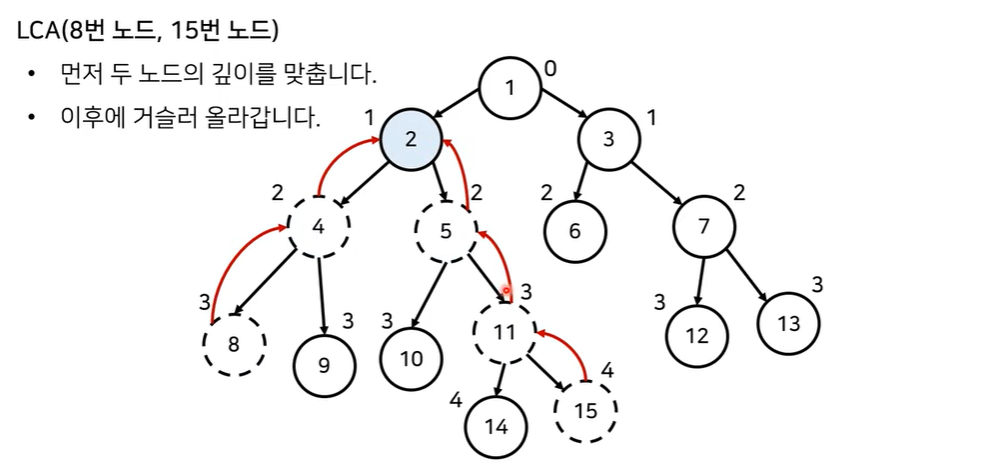
3) 두 노드의 깊이가 동일하게 맞춰졌다면, 동시에 한단계씩 거슬러 올라간다.
그러면 언젠가는 두 포인터가 서로 같아지는 시점이 오는데, 이것이 두 노드의 최소 공통 조상이 된다.
3. 연습문제
11437번: LCA
첫째 줄에 노드의 개수 N이 주어지고, 다음 N-1개 줄에는 트리 상에서 연결된 두 정점이 주어진다. 그 다음 줄에는 가장 가까운 공통 조상을 알고싶은 쌍의 개수 M이 주어지고, 다음 M개 줄에는 정
www.acmicpc.net
4. 풀이
먼저 n개의 노드와 n-1개의 간선으로 구성된 트리를 인접리스트로 저장한다.
트리는 노드가 n개이면 간선은 n-1개임
#n개의 노드와 n-1개의 간선을 가진 트리를 인접리스트로 구성
n = int(input())
tree = [[] for _ in range(n+1)]
for _ in range(n-1): #참고로 트리의 노드가 n개이면 간선은 n-1개
u,v = map(int,input().split())
#트리의 간선은 양방향이기 때문에..
tree[u].append(v)
tree[v].append(u)
다음, DFS로 루트노드부터 탐색을 시작해서, 트리의 깊이를 계산
DFS를 통해, 해당 노드의 부모 노드도 구해야한다.
v에서 시작하고, 시작 노드의 깊이 d = 0이다.
v에 연결된 정점은 tree[v]로 확인 가능하다.
이때, 방문 여부 visited[u]를 체크해서, 방문하지 않았다면, 방문 여부를 표시하고,
그동안 가져온 정점의 깊이 d + 1을 depth[u]에 저장.
여기서 트리는 v에서 u로 내려가는 구조이므로, u의 부모가 v가 된다. 즉, parent[u] = v
그리고 다음 정점 u로 해당 정점의 깊이 d+1을 가져가면서 dfs를 수행
수행이 끝나고 나오면, visited[u] = 0으로 돌려놓고,
다음 dfs 재귀 경로를 탐색할 수 있도록
------------------------------------------------------------------------------------------------------------------------------------------------
tree를 탐색하기 때문에, 이미 방문한 정점은 다시 방문할 이유가 없다.
그래서 visited[u] = 0으로 돌려놓는게 오히려 낭비?
정점을 처음으로 방문한 순간 해당 정점의 깊이는 계산이 되거든
다음과 같이, 1 > 2 > 4 > 8 순서로 탐색하고

다시 되돌아가면.. 8 > 4로 되돌아가고, 4 > 9로 방문할건데..
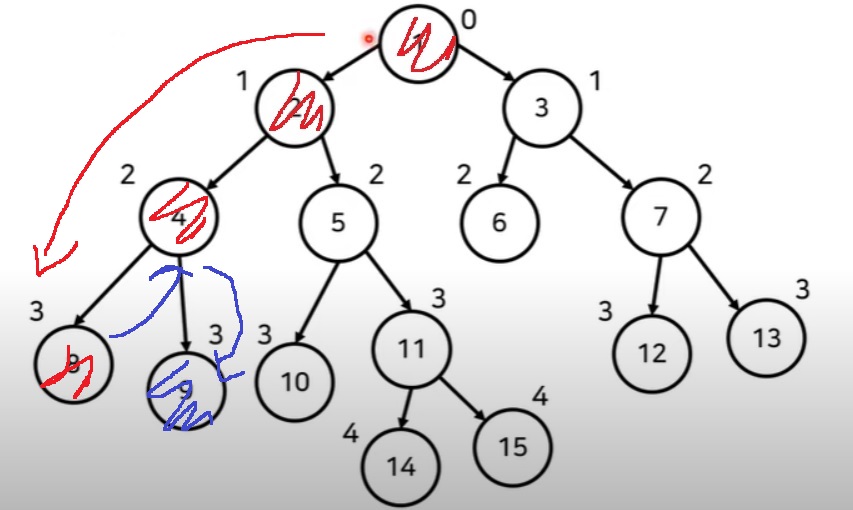
visited[u] = 0으로 하면.. 8번을 다시 방문할 수 있게 된다.
트리 구조라서 사실 8번을 다시 방문할 필요가 없거든
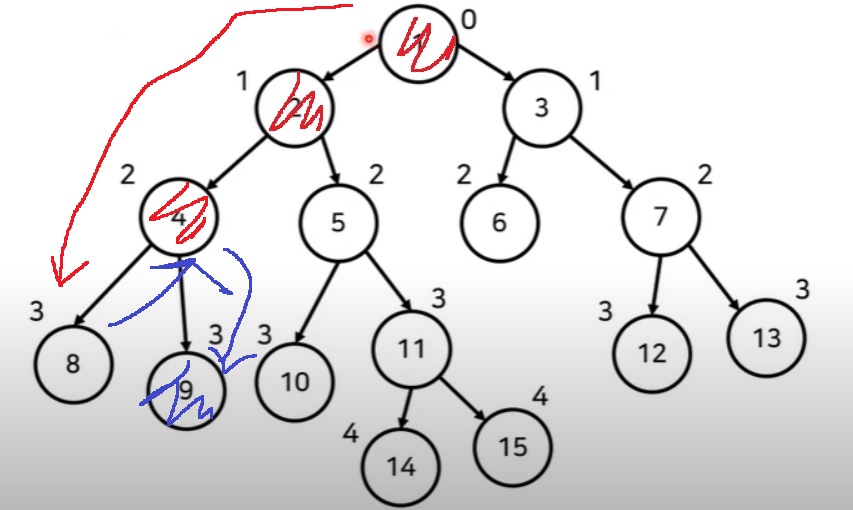
------------------------------------------------------------------------------------------------------------------------------------------------
아무튼 다음은 각 노드의 깊이와 부모를 계산하는 코드
#루트 노드로부터 각 노드의 깊이와 부모를 계산
depth = [0]*(n+1) #각 노드의 루트 노드에서부터 깊이
parent = [0]*(n+1) #각 노드의 부모 노드
visited = [0]*(n+1) #각 노드의 방문 여부
#루트 노드는 1번이고, 깊이는 0으로 초기화
visited[1] = 1
def dfs(v,d):
for u in tree[v]: #v에 연결된 정점 u를 순회하여,
if visited[u] == 0: #u를 아직 방문하지 않았다면..
visited[u] = 1 #u를 방문하고
depth[u] = d + 1 #u의 깊이는 d+1이다.
#트리는 v에서 시작해서 u로 내려가는 구조니까,
#u의 부모가 v가 된다.
parent[u] = v
#그리고 다음 u로 깊이 d+1을 가져가며 dfs 수행
dfs(u, d + 1)
#루트노드는 1번이고, 깊이는 0으로 dfs 시작
dfs(1,0)
다음 u,v 두 정점의 최소 공통 조상을 찾는다.
u,v의 깊이가 다르다면, 깊이가 서로 같을때까지 해당 노드의 부모 노드로 거슬러 올라간다.
depth[u] != depth[v]라면, 깊이가 깊은 노드에 대하여, 해당 노드의 부모 노드를 현재 노드로 갱신한다.
depth[u] > depth[v]라면, u가 더 아래에 있다는 뜻이고, u = parent[u]로 u의 부모를 u로 갱신
depth[u] < depth[v]라면 v가 더 아래에 있다는 뜻이고, v = parent[v]로 v의 부모를 v로 갱신
서로 깊이가 같아지면, u,v가 서로 같아질때까지 두 노드의 부모 노드로 거슬러 올라간다.
u != v라면, u = parent[u], v = parent[v]로 갱신해준다.
------------------------------------------------------------------------------------------------------------------------------------------------------------
dfs말고 bfs로 탐색해도 가능하다.
재귀가 없어서 시간이 더 빠를 수 있다
depth = [0]*(n+1)
parent = [0]*(n+1)
visited = [0]*(n+1)
visited[1] = 1
def bfs(v,d):
queue = deque([(v,d)])
while queue:
v,d = queue.popleft()
for u in tree[v]:
if visited[u] == 0:
depth[u] = d+1
visited[u] = 1
parent[u] = v
queue.append((u,d+1))
bfs(1,0)
------------------------------------------------------------------------------------------------------------------------------------------------------------
#u,v의 최소 공통 조상 찾기
def lca(u,v):
#u,v의 깊이가 서로 다르다면, 깊이를 서로 맞춰준다.
while depth[u] != depth[v]:
#깊이가 더 깊다면, 더 아래에 있다는 뜻이므로,
if depth[u] > depth[v]:
#u가 더 깊다면, u에서 부모로 한단계 거슬러 올라간다.
#u의 부모 parent[u]를 u로 갱신
u = parent[u]
else:
#v가 더 깊다면, v에서 부모로 한단계 거슬러 올라간다.
#v의 부모 parent[v]를 v로 갱신
v = parent[v]
#깊이가 서로 맞춰졌다면, u,v의 부모가 서로 같을때까지 거슬러 올라간다.
while u != v:
#부모가 서로 다르다면, 한단계씩 동시에 거슬러 올라간다.
#u의 부모 parent[u]를 u로 갱신
#v의 부모 parent[v]를 v로 갱신
u = parent[u]
v = parent[v]
#부모가 서로 동일해졌다면, 그 값이 u,v의 최소 공통 조상
return u
이제, 쿼리를 받아 답해준다
m = int(stdin.readline())
for _ in range(m):
u,v = map(int,stdin.readline().split())
print(lca(u,v))
dfs가 너무 오랜만에 했나... 연습좀 해야겠는데
'알고리즘 > 그래프 이론 정복기' 카테고리의 다른 글
| 강한 연결 요소(Strongly connected component)를 구하는 코사라주 알고리즘(kosaraju's algorithm) 배우기 (0) | 2023.09.02 |
|---|---|
| Binary Lifting을 이용한 개선된 최소 공통 조상(Lowest Common Ancestor) 구하는 방법 배우기2 (0) | 2023.08.13 |
| 컴퓨터로 한붓그리기 하는 방법 - 오일러 경로를 찾는 알고리즘 (0) | 2023.02.19 |
| 최대힙, 최소힙 직접 구현하기 (0) | 2022.10.02 |
| 트리 응용 알고리즘 몇가지 - 자손, 루트, 조상찾기, 서브트리 부분순회 - (0) | 2022.09.30 |

