https://www.youtube.com/watch?v=O895NbxirM8
https://kibbomi.tistory.com/201
최소 공통 조상 (LCA, Lowest Common Ancestor)(C/C++)
여러 자료를 참조하면서 LCA를 공부했는데, 어떤 자료는 너무 쉽고 깔끔하지 못하고, 어떤 자료는 난이도가 있고 깔끔하게 설명된 자료였습니다. 그래서 여러 자료를 찾아보며 이해하고, 또 이해
kibbomi.tistory.com
1. 문제
11438번: LCA 2
첫째 줄에 노드의 개수 N이 주어지고, 다음 N-1개 줄에는 트리 상에서 연결된 두 정점이 주어진다. 그 다음 줄에는 가장 가까운 공통 조상을 알고싶은 쌍의 개수 M이 주어지고, 다음 M개 줄에는 정
www.acmicpc.net
이번엔 정점이 10만개이고 쿼리가 10만개 주어진다면, 단순한 선형탐색 O(NM)알고리즘으로는 1.5초 안에 통과하기는 어렵다
https://deepdata.tistory.com/959
최소 공통 조상(Lowest Common Ancestor,LCA)문제 기본 해법 배우기1
https://www.youtube.com/watch?v=O895NbxirM8&list=PLRx0vPvlEmdAghTr5mXQxGpHjWqSz0dgC&index=15 https://www.crocus.co.kr/660 LCA(Lowest Common Ancestor) 알고리즘 LCA(Lowest Common Ancestor) 알고리즘이란? LCA 알고리즘이란 영어 해석 그대
deepdata.tistory.com
2. 더욱 빨리 올라갈 수는 없을까?
기존에는 최소 공통 조상을 알고 싶은 노드 u,v에 대하여 두 노드의 깊이를 동일하게 맞춘 뒤,
서로 같은 위치로 이동할때까지 한칸씩 거슬러 올라가는 전략을 취했지만,
올라가야하는 정점이 1000000000...개씩이나 된다면.. 한단계씩 올라가기에는 올라가다가 시간이 끝날 것이다

그래서 한단계씩 거슬러 올라가지 말고, 조금 더 빠르게 올라가는 방법을 생각해보고 싶다.
만약 15칸을 올라가야한다고 한다면..
2의 거듭제곱으로 8칸 > 4칸 > 2칸 > 1칸씩 거슬러 올라가면 된다.
이렇게 거슬러 올라가면 O(N)에 올라가던 알고리즘을 O(logN)에 거슬러 올라가도록 개선할 수 있다.
하지만 2의 거듭제곱으로 올라가다가 지나칠수도 있는거 아니야?라고 생각할 수도 있는데...
3. 2의 거듭제곱의 합
모든 자연수 n은 2의 거듭제곱의 합으로 표현할 수 있다.
1이상의 자연수 n에 대하여 n = 1이면 명확히 $2^{0}$로 표현되므로 참이다.
어떤 자연수 m에 대해 위 명제가 참이라고 가정한다면, n = 2m, n = 2m+1(m은 1 이상의 자연수)로 나눠서 생각해보자.
m에 대해 참이므로 $m = \sum_{k} 2^{p_{k}}$을 만족하는 $p_{k}$는 무수히 많고 모두 서로 다르다.
n = 2m이면, $n = 2m = \sum_{k} 2^{p_{k} + 1}$이므로, n에 대해서 참이다.
마찬가지로 n = 2m+1이면 $n = 2m + 1 = 2^{0} + \sum_{k} 2^{p_{k} + 1}$로 표현할 수 있다.
그러므로 수학적 귀납법에 의해 모든 자연수 n은 2의 거듭제곱의 합으로 표현된다.
이러한 사실은 최소 공통 조상을 찾기 위해 2의 거듭제곱씩 올라가도 된다는 것을 보여준다.
4. 알고리즘
메모리를 조금 더 사용해서 각 노드에 대하여 $2^{i}$번째 부모의 정보를 기록하도록 한다.
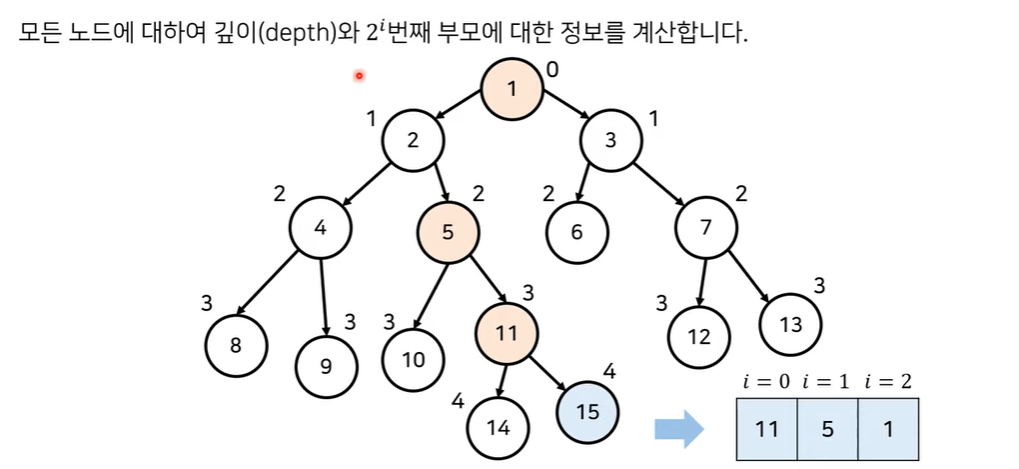
위의 예시에서 15번 노드의 한단계 위 부모는 11이고, 2단계 위 부모는 5이고 4단계 위 부모는 1이다.
각 노드에 대해 깊이와 한 단계 위의 부모를 이전 기본 알고리즘에서 구한 대로 DFS를 이용해 구하고,
이를 이용해 다이나믹 프로그래밍으로 각 노드의 모든 $2^{i}$번째 부모를 구하도록 한다.
노드의 개수가 N개이면 각 노드에 대하여 logN만큼의 공간이 필요하므로, 총 NlogN의 공간복잡도가 필요하다.
공간을 많이 쓰는 만큼, 더 많은 정보를 활용하여 빠르 최소 공통조상을 찾으므로 시간복잡도를 향상시키는 trade off 관계가 있다.
5. 예시로 알아보는 알고리즘
다음 그래프에서 13번 노드와 15번 노드의 최소 공통 조상을 찾는다면..?

먼저 두 노드의 깊이를 동일하게 맞춘다.
올라가야하는 크기를 알아낸다면, 이로부터 2의 거듭제곱꼴로 빠르게 올라가도록 한다.
이후에 거슬러 올라갈때도 마찬가지로 2의 거듭제곱꼴로 빠르게 올라간다.

현재 11과 13은 3만큼 거슬러 올라가야 만날 수 있는데, 3 = 2 + 1이므로 2단계 올라가고,
1단계 올라가면 시간을 단축시킬 수 있다.

노드의 개수가 많을수록 올라가야하는 노드 수가 많아지므로, 2의 거듭제곱꼴로 올라간다면
1단계씩 거슬러 올라가는거에 비해 극적인 시간 개선이 느껴진다.
6. 구현 예시
세그먼트 트리를 이용할 수도 있고 다이나믹 프로그래밍을 이용할 수도 있다.
매 쿼리마다 부모를 거슬러 올라가는 시간복잡도가 O(logN)이므로,
M개 쿼리의 최소 공통 조상을 찾는 총 시간복잡도는 O(MlogN)으로 O(MN)에서 많이 개선된다.
먼저 트리를 구성한다.
트리는 노드 수가 N개이면 간선의 수는 N-1개이다.
#Binary Lifting + DP를 이용한 최소 공통 조상 찾기
#2의 거듭제곱꼴로 부모 노드를 거슬러 올라간다
#트리 구성
n = int(input())
tree = [[] for _ in range(n+1)]
#트리의 노드 수가 N개이면 간선의 수는 N-1개
for _ in range(n-1):
u,v = map(int,input().split())
tree[u].append(v)
tree[v].append(u)
다음 dfs를 이용해 각 노드의 깊이, 부모 노드 정보를 구한다.
이전과 다른 점은 부모 노드 정보를 2차원 배열로 구성한다.
parent[u][i] = u 노드의 $2^{i}$번째 부모 노드
parent[u][0]는 u 노드의 한단계 위 부모 노드를 말한다.
그러므로 dfs를 이용해 각 노드의 깊이, parent[u][0]을 모두 구해놓는다.
#dfs를 이용해 루트 노드부터 각 노드의 깊이, 부모 노드 정보를 구한다.
max_two = 21 #2^20 = 약 100만(최대 노드 수가 약 100만개 정도라고 가정)
depth = [0]*(n+1) #노드의 깊이
#노드의 부모
#parent[u][i] = u 노드의 2^i번째 부모 노드
parent = [[0]*(max_two) for _ in range(n+1)]
visited = [0]*(n+1)
#루트 노드가 1번
visited[1] = 1
#v노드가 깊이 d이고, dfs 수행
def dfs(v,d):
#v에 연결된 u 노드 정보를 파악
for u in tree[v]:
if visited[u] == 0: #u를 아직 방문하지 않았다면..
visited[u] = 1 #u를 방문처리
depth[u] = d + 1 #u는 v 한단계 아래니까, 깊이는 v의 깊이 + 1
parent[u][0] = v #v에서 u로 내려왔으므로, u의 부모는 v
dfs(u,d + 1) #다음 u로 깊이 d+1을 가지고 dfs수행
이제 모든 노드의 모든 2의 거듭제곱꼴 부모를 다이나믹 프로그래밍을 이용하여 구한다.
parent[i][0]들 정보만 있는데, 이로부터 구할 수 있나??
j번 노드의 $2^{i}$번째 부모는...?

j에서 $2^{i}$까지 거슬러 올라가는 것은 j에서 $2^{i-1}$만큼 올라가고, 거기서 $2^{i-1}$만큼 올라간 것과 같다.
j의 $2^{i-1}$번째 부모 parent[j][i-1]은 j에서 $2^{i-1}$만큼 올라간것이다.
또한 이 지점의 노드 parent[j][i-1]에서 $2^{i-1}$만큼 거슬러 올라간 부모는.. parent[parent[j][i-1]][i-1]을 나타낸다.
그러므로, j에서 $2^{i}$만큼 거슬러 올라간 부모 parent[j][i] = parent[parent[j][i-1][i-1]이 성립한다.
#먼저 모든 노드의 한단계 위 부모를 구한다.
dfs(1,0)
#다이나믹 프로그래밍을 이용해 모든 노드의 2의 거듭제곱꼴 부모를 구한다.
def dp_parent(parent):
for i in range(1,max_two): #i = 0은 구해졌고, i = 1 ~ max_two-1까지
for j in range(1,n+1): #j는 노드번호로 1부터 n까지
#j에서 2^i-1올라가고 2^i-1올라간 것은 j에서 2^i만큼 올라간것과 같다.
#j >> parent[j][i] >> parent[parent[j][i-1]][i-1]로 유도된 부모 관계 점화식
parent[j][i] = parent[parent[j][i-1]][i-1]
다음으로 a,b의 최소 공통조상을 찾는다.
먼저 b의 깊이가 항상 더 깊은 노드가 되도록 설정하고
if depth[a] > depth[b]:
a,b = b,a
더 깊은 노드에서 서로 노드 깊이가 동일하도록 맞춰준다.
여기서 올라올때도 2의 거듭제곱으로 올라오는데..
최대로 설정한 2의 거듭제곱 지수 max_two-1에서 0까지 감소시켜가면서,
두 노드의 깊이 차이 depth[b] - depth[a]가 2의 i제곱보다 크거나 같다면, 일단 거슬러 올라간다.
for i in range(max_two-1,-1,-1):
if depth[b] - depth[a] >= (2**i):
b = parent[b][i]
for문을 전부 돌면 두 노드 깊이 차이가 동일해질 것이다.
왜냐하면 위에서 증명했듯이 모든 자연수 n은 2의 거듭제곱 합으로 표현되기 때문이다.
정말로 그런지 예를 들어 생각해보자.
차이가 13으로 홀수라면..?
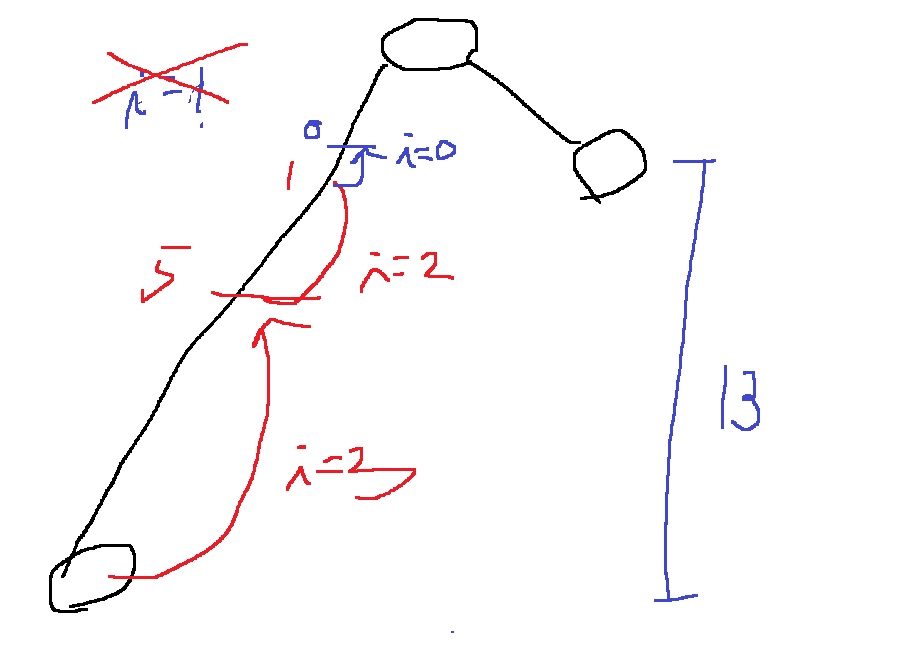
차이가 14로 짝수라면??

반복문이 끝나서 두 노드 깊이가 동일해질때
서로 노드가 같은 노드라면 그것이 최소 공통 조상이고 바로 return
그렇지 않다면 두 노드가 서로 동일해질때까지 2의 거듭제곱만큼 거슬러 올라간다.
if a == b:
return a
for i in range(max_two-1,-1,-1):
if parent[a][i] != parent[b][i]:
a = parent[a][i]
b = parent[b][i]
위와 같이 최대 지수 max_two-1부터 0까지 감소시켜가면서 2의 i제곱 부모가 서로 다르다면 2의 i제곱만큼 거슬러 올라가고
서로 같다면 올라가지 않는다
이렇게 올라가면 반복문이 끝날때 언제나 한단계 위 부모가 바로 최소 공통 조상이 되는데...
이게 되게 신기하네? 예를 들어 한번 생각해보자.
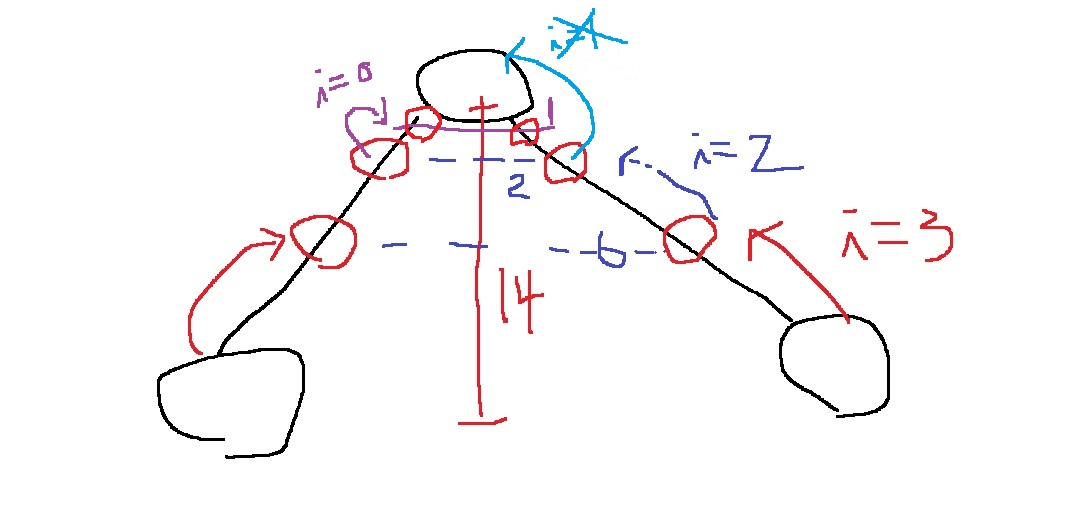
최소 공통 조상까지 짝수인 14차이일때, i = 3이면 두 노드 부모가 다르니까 일단 8만큼 올라가고
그러면 6만큼 남아있는데 i = 2이면 두 노드 부모가 다르니까 일단 4만큼 올라가고..
그러면 2만큼 남아있는데 i = 1이면 2만큼 올라가면 두 노드 부모가 같으니까, 올라가지 않는다

그러다가 i = 0이 된다면, 두 노드 부모가 다르므로, 1칸만 올라간다.
그러면 1칸 위 부모가 최소 공통 조상이 된다.
홀수인 13차이일때는 어떨지 생각해보면..
i = 3일때 8만큼 올라가면 두 노드 부모가 다르니 올라가고..
그러면 차이가 5 남았는데 i = 2일때 두 노드 부모가 다르니 올라가고
그러면 차이가 1 남았는데, i = 1이면 2만큼 올라가야하는데 2만큼 올라가면 초기 부모 노드 값이 0으로 되어 있으니
서로 같아서 올라가지 않는다

마찬가지로 i = 0에서 차이가 1 남은 상황에서 올라가면 두 노드 부모가 같으니 올라가지 않는다.
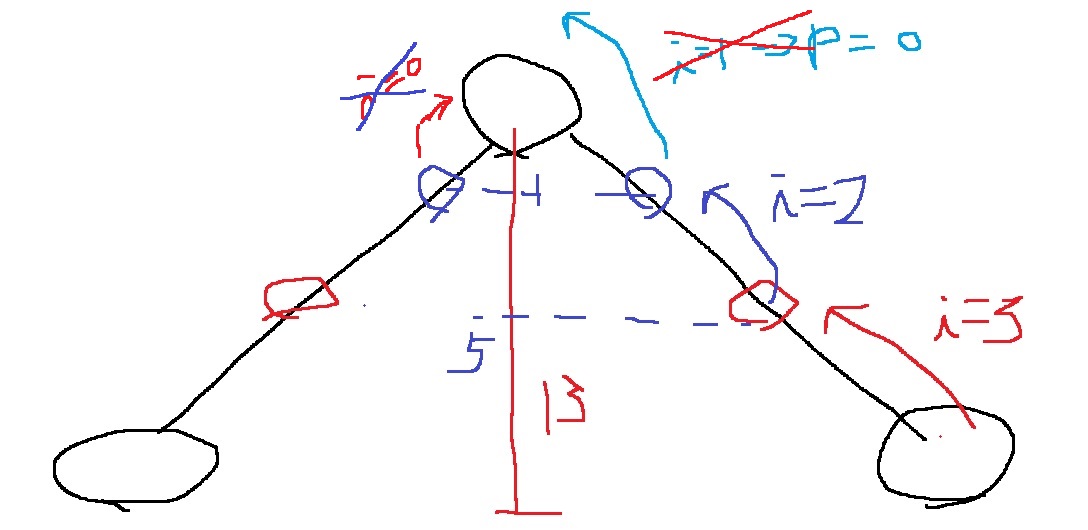
그러므로 어떤 경우에도 for문이 끝나면 1단계 전 값으로 나온다.
그래서 1단계 위 부모 노드 값이 바로 a,b의 최소 공통 조상이 된다.
#두 노드 a,b의 최소 공통 조상을 찾는다
def lca(a,b):
#b의 노드 깊이가 더 깊도록 맞춰준다.
if depth[a] > depth[b]:
a,b = b,a
#max_two - 1에서 0까지 2의 거듭제곱 지수 i를 감소시켜가면서,
#두 노드의 깊이 차이가 2의 i제곱보다 크거나 같다면,
#일단 2의 i제곱만큼 거슬러 올라간다
for i in range(max_two-1,-1,-1):
if depth[b] - depth[a] >= (2**i):
b = parent[b][i]
#반복문이 끝나면 두 노드의 깊이 차이는 0이 된다.
#왜냐하면 모든 자연수는 2의 거듭제곱 합으로 표현되기 때문이다.
#두 노드 깊이 차이가 짝수이냐 홀수이냐에 따라..
#(짝수) 14 >>(i = 3) 6 >> (i = 2) 2 >> (i = 1) 0
#(홍수) 13 >>(i = 3) 5 >> (i = 2) 1 >> (i = 0) 0
#두 노드가 동일한 깊이가 되었을때, 서로 같은 노드라면 바로 return
if a == b:
return a
#max_two - 1에서 0까지 2의 거듭제곱 지수 i를 감소시켜가면서,
#2^i만큼 위 부모 노드가 서로 다르다면 거슬러 올라간다.
for i in range(max_two-1,-1,-1):
if parent[a][i] != parent[b][i]:
a = parent[a][i]
b = parent[b][i]
#신기하게도 반복문이 끝나면 바로 1단계 위 부모노드가 최소 공통 조상이 된다.
#최소공통조상까지 차이가 짝수이냐 홀수이냐에 따라..
#(짝수) 14 >>(i = 3) 6 >> (i = 2) 2 >> (i = 0) 1
#(홀수) 13 >>(i = 3) 5 >> (i = 2) 1
return parent[a][0]
이제 모든 쿼리에 답을 해주면 된다.
'알고리즘 > 그래프 이론 정복기' 카테고리의 다른 글
| 저울의 무게 비교를 그래프로 바꿔서 최단 거리 알고리즘으로 해결(플로이드 워셜, 그래프 탐색) (0) | 2023.09.07 |
|---|---|
| 강한 연결 요소(Strongly connected component)를 구하는 코사라주 알고리즘(kosaraju's algorithm) 배우기 (0) | 2023.09.02 |
| 최소 공통 조상(Lowest Common Ancestor,LCA)문제 기본 해법 배우기1 (0) | 2023.08.07 |
| 컴퓨터로 한붓그리기 하는 방법 - 오일러 경로를 찾는 알고리즘 (0) | 2023.02.19 |
| 최대힙, 최소힙 직접 구현하기 (0) | 2022.10.02 |

