1. 픽의 정리(pick's theorem)
좌표가 모두 정수인 점을 격자점(lattice)이라고 부른다.
2차원 좌표평면에서 모든 꼭짓점이 격자점인 다각형이 자기 자신이 교차하지 않을때(not self-interaction), 넓이가 A이고
내부에 있는 격자점의 개수가 I이며 둘레(변)에 있는 격자점의 개수가 B이면...
$$A = I + \frac{B}{2} - 1$$이 성립한다.
여러 경우의 수로 나눠서 증명하는데, 조금 까다롭다... 읽어보는걸로 만족하고 생략
https://www.youtube.com/watch?v=GTeZd_IdcoY
영상이 설명을 잘해주고 있는데...
주어진 다각형을 내부의 격자점 수가 0개이고 경계선 위 격자점의 개수가 3개인 삼각형으로 도형을 모두 분할할 수 있고,
이 삼각형들의 넓이와 격자점 수를 세서 증명하는 것 같다..
또한 일반적으로 2차원에서 성립하고 고차원으로 일반화가 잘 되지는 않는것 같다.
2. 연습문제1
7694번: Triangle
The input test file will contain multiple test cases. Each input test case consists of six integers x1, y1, x2, y2, x3, and y3, where (x1, y1), (x2, y2), and (x3, y3) are the coordinates of vertices of the triangle. All triangles in the input will be non-d
www.acmicpc.net
3. 풀이
주어진 삼각형 내부의 격자점 수를 세는 문제.
도형의 둘레에 있는 격자점은 세지 마라고 했으니, A = I + B/2 - 1에서 I를 구하는 문제다.
세 점이 주어지면 넓이야 신발끈 공식이나 두 벡터의 외적으로 구할 수 있는데 둘레에 있는 격자점 개수를 어떻게 세야할지 문제다.
하나하나 세자니 15000*15000으로 여러 테스트케이스를 1초안에 계산할리는 없을거고
3-1) 둘레에 있는 격자점의 개수
근데 여러 생각을 해보니까 두 점 (x1,y1), (x2,y2)가 주어질때 기울기를 이용해서 개수를 바로 알 수 있다는걸 알아냈다.
구체적으로 (y2-y1)과 (x2-x1)의 최대공약수 +1개 만큼 존재한다는 것을 관찰했다.

위와 같이 (0,0)과 (5,5)가 주어졌을때 (5-0), (5-0)은 5,5이고 최대공약수는 5이다.
파란색 동그라미 부분만큼 최대공약수로 세어지고, 첫 시작점 (0,0) 1개를 더해서 총 6개가 있다.
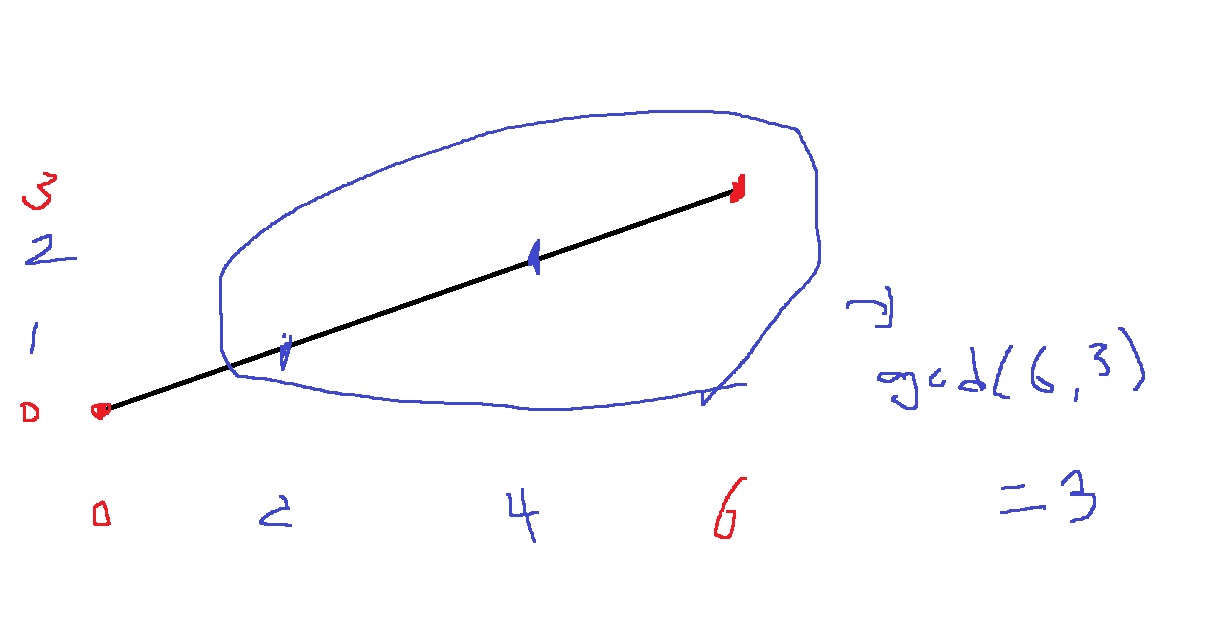
기울기가 1이 아니더라도... (0,0)과 (6,3)사이 격자점의 개수는 6과 3의 최대공약수인 3개가 파란색 동그라미 부분에 있고
나머지 시작점 (0,0) 1개 해서 총 4개가 있다
일반적으로 정수 a,b,c,d에 대해 (a,b), (c,d)를 이은 선분위의 격자점의 개수는 $$gcd(c-a,d-b)+1$$이다.
두 선분의 방정식은 $y = \frac{d-b}{c-a}(x-a) + b$이다. 여기서 c-a가 0이 아니라고 가정하자.
최대공약수 g = gcd(c-a,d-b)라고 한다면, c-a = gp, d-b = gq라고 나타낼 수 있다. 여기서 p,q는 서로소이다.
그러면 선분의 방정식은 $$y = \frac{q}{p}(x-a) + b$$
그러므로 정수 x에 대하여 y가 정수일려면 (x-a)가 p의 배수여야한다.
여기서 x는 $a \leq x \leq c$이므로 $0 \leq x-a \leq c-a$이고, c-a = gp이므로 $$0 \leq x-a \leq gp$$
그런데 x-a가 p의 배수이므로 부등식을 p로 나누면 0부터 g까지의 정수의 개수와 동일하다.
따라서 그것을 만족하는 x-a의 개수는 0부터 gp까지는 g+1개만큼 존재하게 된다.
그러므로, (a,b),(c,d) 사이 격자점의 개수는 gcd(c-a,d-b) + 1개이다.
-------------------------------------------------------------------------------------------------------------------------------------------------------
3-2) 실수 연산을 피하는 방법
모든 프로그래밍의 기본은 실수 연산은 피하는게 좋다. 기본적으로 오차가 있으니까
주어진 다각형이 삼각형이기 때문에
삼각형의 넓이는 신발끈 공식을 사용하거나, A를 기준으로 AB, AC 벡터를 구하고 두 벡터의 외적을 이용해 구할 수 있는데..
https://deepdata.tistory.com/956
기하학 알고리즘의 기본 - 두 벡터의 외적(cross product)에 대하여
https://gaussian37.github.io/math-la-cross-product/ 벡터의 외적이란? gaussian37's blog gaussian37.github.io https://cp-algorithms.com/geometry/basic-geometry.html#definition_1 Basic Geometry - Algorithms for Competitive Programming Basic Geometry In
deepdata.tistory.com
https://deepdata.tistory.com/733
평면 상의 다각형의 넓이 구하는 신발끈 공식 구현
1. 문제 2166번: 다각형의 면적 (acmicpc.net) 2166번: 다각형의 면적 첫째 줄에 N이 주어진다. 다음 N개의 줄에는 다각형을 이루는 순서대로 N개의 점의 x, y좌표가 주어진다. 좌표값은 절댓값이 100,000을
deepdata.tistory.com
기본적으로 도형의 넓이는 두 방법 모두 $A = \frac{x}{2}$ 형태로 되어 있다
전체 좌표들의 곱의 합 x를 2로 나눈 형태이고.. 픽의 정리도 A = I + B/2 - 1이므로, 양변에 2를 곱한다면?
$$2A = 2I + B - 2$$가 된다.
2A는 좌표들의 곱의 합 x이므로, 이 x랑 B만 구하면 2I를 구할 수 있다.
x자체는 마지막에 2로 안나누기만 하면 된다
#area of triangle1
x = [x1,x2,x3,x1]
y = [y1,y2,y3,y1]
def area(x,y):
a = 0
for i in range(3):
a += x[i]*y[i+1]
a -= y[i]*x[i+1]
if a < 0:
a = -a
return a
#area of triangle2
x = [x2-x1,y2-y1]
y = [x3-x1,y3-y1]
def area(x,y):
return abs(x[0]*y[1] - x[1]*y[0])
게다가 2I는 무조건 정수이기 때문에 마지막에 정수 나눗셈을 하면 정수연산만으로 답을 구할 수 있다.
변 위에 있는 격자점의 개수는 위에서 설명한대로, 두 점 (a,b), (c,d)에 대해 (c-a,d-b)의 최대공약수를 구하고 1을 더하면 된다.
그런데 세 점 (x1,y1), (x2,y2)와 (x2,y2), (x3,y3)와 (x1,y1), (x3,y3)에 대해 각각 구하면 꼭짓점의 수 3개를 중복해서 센다.
그러므로 각각에서 개수를 셀때 양 선분의 끝점의 수 2개를 빼준 상태로 세주자.
그리고 전부 더해서 마지막에 3을 더한다면 중복해서 세지 않을 것이다.
from sys import stdin
#pick's theorem
#A = I+B/2-1 >>> 2A = 2I+B-2
#2I = 2A+2 - B >>> I = (2A+2-B)//2
#area of triangle
#정수 연산을 위해 1/2을 하지 않는다
def area(x,y):
return abs(x[0]*y[1] - x[1]*y[0])
#count lattice in edge
#num of (a,b),(c,d) = gcd(c-a,d-b)+1
def count_lattice_edge(x,y):
a = abs(y[0]-x[0])
b = abs(y[1]-x[1])
while b != 0:
a,b = b,a%b
return a - 1
while 1:
x1,y1,x2,y2,x3,y3 = map(int,stdin.readline().split())
if x1 == 0 and y1 == 0 and x2 == 0 and y2 == 0 and x3 == 0 and y3 == 0:
break
else:
x = [x2-x1,y2-y1]
y = [x3-x1,y3-y1]
a = area(x,y)
b = count_lattice_edge((x1,y1),(x2,y2)) + count_lattice_edge((x2,y2),(x3,y3)) + count_lattice_edge((x3,y3),(x1,y1)) + 3
#pick's theorem
print((a+2 - b)//2)
4. 연습문제2
6384번: Area
The output for every scenario begins with a line containing “Scenario #i:”, where i is the number of the scenario starting at 1. Then print a single line containing I, E, and A, the area A rounded to one digit after the decimal point. Separate the thre
www.acmicpc.net
5. 풀이
위 문제는 삼각형만 나오지만 이번엔 일반화된 다각형이 나온 문제다.
주어지는 좌표값은 좌표가 아니라 dx,dy로 해당 방향으로 로봇이 움직인다는 뜻이기 때문에
시작 a = 0, b = 0으로 해두고 a+dx,b+dy로 계속해서 누적해가지고 (x,y)를 구해줘야한다.
또한 시계 반대방향으로 움직인다고 했기 때문에 신발끈 공식을 적용하기에도 적절하다.
그러므로 위에서 설명한대로 이 역시 정수 연산만으로 2A = 2I + B - 2를 이용해 넓이, 내부 점, 경계선 점을 모두 구할 수 있다.
또한 몰랐는데, 경계선 상 점을 셀때 gcd(c-a,d-b)-1로 구했는데 c-a,d-b중 어느 하나라도 음수라면 문제 생길 수 있다
그러니까 c-a = -1, d-b = 0이라면, gcd(-1,0) = -1로 나와서 -2를 return하는 문제가 생길 수 있다..
그래서 gcd(abs(c-a), abs(d-b))로 구해줘야한다..
처음에는 운좋게 abs()를 했었네 하하
또한 다각형이기 때문에 마지막에 e += 3이 아니라, e += (꼭짓점 수)를 해줘야지..
from sys import stdin
def area(x,y):
a = 0
for i in range(m):
a += x[i]*y[i+1]
a -= y[i]*x[i+1]
if a < 0:
a = -a
return a
def count_lattice_edge(a,b):
while b != 0:
a,b = b,a%b
return a-1
T = int(stdin.readline())
for t in range(1,T+1):
m = int(stdin.readline())
x = []
y = []
a = 0
b = 0
for _ in range(m):
dx,dy = map(int,stdin.readline().split())
a += dx
b += dy
x.append(a)
y.append(b)
x.append(x[0])
y.append(y[0])
a = area(x,y)
e = 0
for i in range(m):
e += count_lattice_edge(abs(y[i+1]-y[i]),abs(x[i+1]-x[i]))
e += m
i = a+ 2 - e
print(f'Scenario #{t}:')
print(i//2,e,a/2)
print()
참고
https://cp-algorithms.com/geometry/picks-theorem.html#proof
Pick's Theorem - area of lattice polygons - Algorithms for Competitive Programming
Pick's Theorem A polygon without self-intersections is called lattice if all its vertices have integer coordinates in some 2D grid. Pick's theorem provides a way to compute the area of this polygon through the number of vertices that are lying on the bound
cp-algorithms.com
https://namu.wiki/w/%EA%B2%A9%EC%9E%90%EC%A0%90
격자점 - 나무위키
(A, B형 당시의 수능 수학 시험지는) 29+1 체제를 하고 있었는데 이 앞의 29문제는 정말 말도 못 하게 쉬워요. 제가 예전에 현장에서 가르쳤던 애들 중 잘하는 애들은 거의 30~40분 안에 다 풀었고, 나
namu.wiki
https://math.stackexchange.com/questions/628117/how-to-count-lattice-points-on-a-line
How to count lattice points on a line.
How can we count the number of lattice point on a line, given that the endpoints of the lines are themselves lattice points? I really can't think of how counting lattice points would work, so please
math.stackexchange.com
'기하학' 카테고리의 다른 글
| 볼록 껍질(convex hull) 구하는 graham scan 알고리즘 배우기 (0) | 2023.09.07 |
|---|---|
| 각도 구하는 math.atan, math.atan2 사용법 익히기 (0) | 2023.09.01 |
| 선분의 길이가 주어질때 볼록 다각형(conver polygon)이 될 조건 (0) | 2023.08.25 |
| 정육면체가 쌓인 3차원 도형의 겉넓이를 구하는 방법 (0) | 2023.08.25 |
| 모든 좌표까지 맨해튼 거리 합이 최소가 되는 위치를 구하는 방법 (0) | 2023.08.24 |

