1. 문제
16931번: 겉넓이 구하기
크기가 N×M인 종이가 있고, 종이는 1×1크기의 칸으로 나누어져 있다. 이 종이의 각 칸 위에 1×1×1 크기의 정육면체를 놓아 3차원 도형을 만들었다. 종이의 각 칸에 놓인 정육면체의 개수가 주어
www.acmicpc.net
2. 풀이
위,아래, 앞,뒤,왼쪽,오른쪽에서 보이는 면의 개수를 전부 더하면 될 것이며
면의 개수는 어떻게 구하지?
n*m 크기의 바닥 아래에 정육면체를 쌓았을때,
위나 아래에서 봤을때는? 당연히 n*m개씩 보일 것이다.

왼쪽과 오른쪽에서 봤을때는?
위 그림이
1 3 4
2 2 3
1 2 4
와 같이 주어지는데, 왼쪽에서 본다면,
1 3 4
>>>>>> 2 2 3
1 2 4
처럼 상상해본다면... 배열에서 각 행마다 최댓값을 선택하면 될 것이다.
그러니까 왼쪽에서 볼때 1행에서는 4개, 2행에서는 3개, 3행에서는 4개
생각해보면 오른쪽도 마찬가지로 각 행마다 최댓값 원소 개수만큼 보인다.
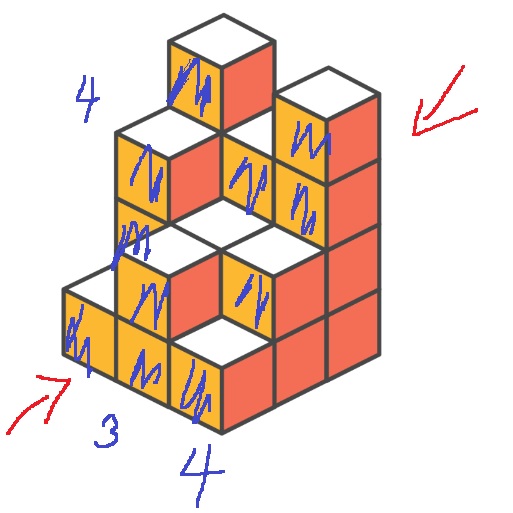
앞 뒤로 봤을때는??
1 3 4
2 2 3
1 2 4
↑
↑
↑
이렇게 본다고 생각해봤을때, 각 열마다 최댓값 원소만큼 보일 것이다.
그러니까 1열에는 2개, 2열에는 3개, 3열에는 4개
이는 뒤로 볼때도 마찬가지다.
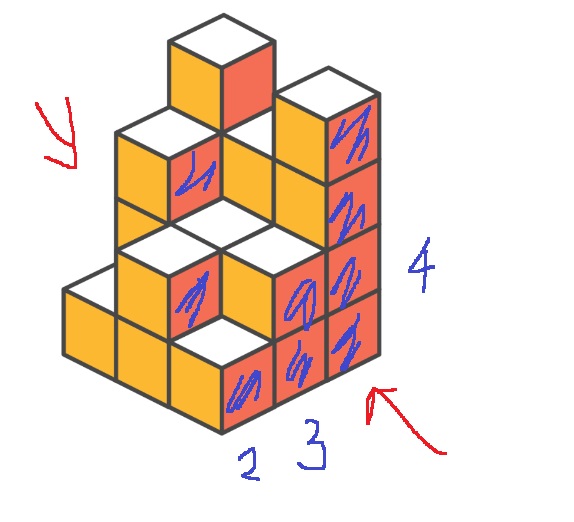
그러면 위, 아래에서 볼때 3*3*2 = 18개
왼쪽, 오른쪽에서 볼때 (4+3+4)*2 = 22개
앞, 뒤로 볼때, (2+3+4)*2 = 18개
해서 겉넓이가 58인가? 했는데 답은 60이더라고... 2개를 못센건가?? 찾는 와중에

최대 높이가 동일하면, 저렇게 초록색 부분 두 부분이 가려져서 못세더라...
근데 계속 관찰하다보니까 번뜩이는 아이디어?가 생각난게
예를 들어 왼쪽에서 볼때, 3행에 4개가 보인다는 것을 어떻게 아는가?
왼쪽부터 순회해서, 처음에 1개를 읽고
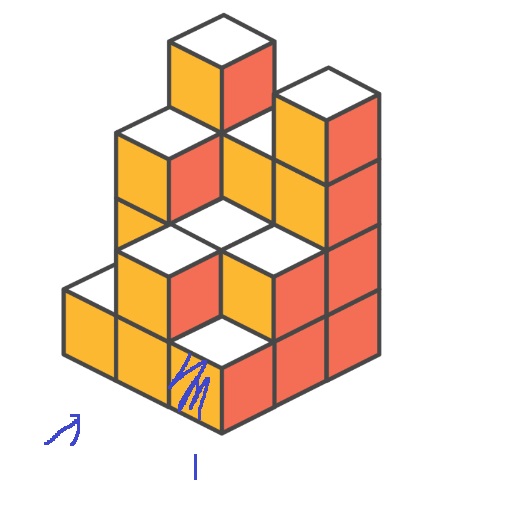
그 다음 원소는 2인데, 그 다음 원소까지 새롭게 보여지는 겉면적의 수는, 이전에 보인 1개를 제외한 1개가 된다

그리고 그 다음 원소 4를 읽는데, 이제 새롭게 보여지는 겉면적의 수는, 이전까지 보인 총 개수 2개를 제외한 2개가 된다
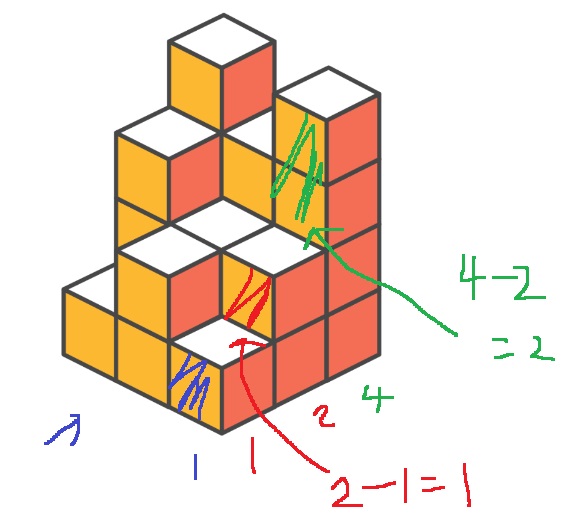
그러면 왼쪽에서 볼때 총 겉면적의 수는, 고정된 행 n에 대하여, 0부터 m-1까지 순회해서 인접한 원소끼리의 차이를 더해가면 되는게 아닐까?
오른쪽에서 볼때 총 겉면적의 수는? 고정된 행 n에 대하여, m-1부터 0까지 순회해서 인접한 원소끼리 차이를 더해간다
앞에서 볼때 총 겉면적의 수는? 고정된 열 m에 대하여, n-1부터 0까지 순회해서 인접한 원소끼리 차이를 더해간다
뒤에서 볼때 총 겉면적의 수는? 고정된 열 m에 대하여 0부터 n-1까지 순회해서 인접한 원소끼리 차이를 더해간다
위와 아래에서 볼때는 방해하는게 없이 n*m 면적 수만큼 보이기 때문에 시작 넓이는 2*n*m으로 시작하면 된다
인접한 원소끼리 차이가 음수면 뭐냐고?
당연히 해당 방향에서 볼때 그 만큼 가려진 수라는 의미이므로, 더하지 않아도 된다

오른쪽에서 볼때, 3행에서 3열 원소, 2열 원소, 1열 원소로 순회해가는데 처음에 4개가 보여서 4를 더하고,
2열로 가는데 2개가 있다는데, 처음에 4개 보이니까 2-4 = -2개가 보인다?
오른쪽에서 볼때 3열 원소에 2개가 가려졌다는 의미잖아
그러니까 인접한 원소끼리 차이가 양수면 더해가고, 음수면 continue로 넘기면 되겠다.
#정육면체를 쌓은 도형의 겉넓이 구하기
from sys import stdin
n,m = map(int,stdin.readline().split())
maps = [list(map(int,stdin.readline().split())) for _ in range(n)]
answer = 0
#위,아래
answer += 2*(1*n*m)
#해당방향으로 순회하는데, 인접한 원소끼리 차이가 양수면 그 차이만큼을 더해나가면 된다
#왼쪽, 오른쪽
for y in range(n):
answer += maps[y][0]
#고정된 행 y에 대하여 각 열을 왼쪽에서 오른쪽으로 순회
for x in range(1,m):
if maps[y][x] - maps[y][x-1] > 0:
answer += (maps[y][x] - maps[y][x-1])
answer += maps[y][m-1]
#고정된 행 y에 대하여 각 열을 오른쪽에서 왼쪽으로 순회
for x in range(m-2,-1,-1):
if maps[y][x] - maps[y][x+1] > 0:
answer += (maps[y][x] - maps[y][x+1])
#앞,뒤
for x in range(m):
answer += maps[0][x]
#고정된 열 x에 대하여 각 열을 위에서 아래로 순회
for y in range(1,n):
if maps[y][x] - maps[y-1][x] > 0:
answer += (maps[y][x] - maps[y-1][x])
answer += maps[n-1][x]
#고정된 열 x에 대하여 각 열을 아래에서 위로 순회
for y in range(n-2,-1,-1):
if maps[y][x] - maps[y+1][x] > 0:
answer += (maps[y][x] - maps[y+1][x])
print(answer)
사람이 어떻게 구하는지 그 과정을 그대로 코딩하면 되는거..
'기하학' 카테고리의 다른 글
| 다각형 내부의 격자점 수를 셀 수 있을까 - 픽의 정리(pick's theorem) + (선분에 있는 격자점의 개수 세는 방법) (0) | 2023.08.31 |
|---|---|
| 선분의 길이가 주어질때 볼록 다각형(conver polygon)이 될 조건 (0) | 2023.08.25 |
| 모든 좌표까지 맨해튼 거리 합이 최소가 되는 위치를 구하는 방법 (0) | 2023.08.24 |
| 모든 좌표 쌍의 맨해튼 거리의 합을 효율적으로 구하는 방법 (0) | 2023.08.24 |
| 기하학의 사칙연산인 CCW(Counter-ClockWise) 알고리즘 배우기 (0) | 2023.08.05 |

