1. 군집(community)
군집은 다음 두가지 조건을 모두 만족하는 하나의 node 집합이다.
1) 집합에 속하는 node 사이에 충분히 많은 link가 있다.
2) 그러한 집합에 속하는 node와 속하지 않는 node 사이에는 충분히 적은 link가 있다.
딱 봐도 수학적인 정의는 아니지만 눈으로 보기에 군집을 구별하는 것은 쉽다

2. example
SNS의 군집들은 사회적으로 의미있는 사회적 무리(Social circle)를 형성
실제 SNS에서는 돈을 받고 팔로워를 늘려주는 경우도 많다.

하나의 조직 내 분란으로 인해 군집이 형성
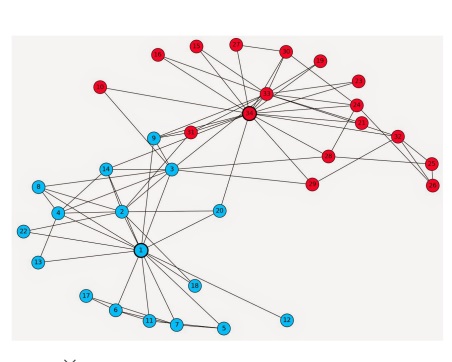
내분으로 동아리가 둘로 나뉘었다는데??
회사 내 이메일 네트워크나 보고체계를 분석하여 그래프로 나타내면 회사 커뮤니케이션이 얼마나 효율적인지 알아볼 수 있음
키워드-광고주 그래프에서 관심있는 키워드에 광고주끼리 군집이 형성
인접행렬(adjacency matrix)은 하나의 그래프에서 node i와 j사이 link의 수를 (i,j)원소로 가지는 행렬이다.

뉴런간 연결 그래프로부터 비슷한 기능을 하는 뉴런들이 군집을 형성한다는 것을 파악할 수 있음

3. community detection
주어진 그래프를 여러 군집으로 ‘잘’ 나누는 문제
각 node가 하나의 군집에 속하도록 나눈다.
비지도 기계학습인 clustering은 데이터의 instance로 주어지는 feature 벡터들을 grouping
community detection은 그래프 내 node들을 grouping
둘이 큰 차이는 없는듯?
4. local clustering coefficient
특정 node V의 모든 이웃쌍중에서 직접 연결된 이웃쌍의 비율

node 1의 이웃의 집합 {2,3,4,5}
이웃의 순서쌍은 (2,3), (2,4), (2,5), (3,4), (3,5), (4,5)
이웃쌍을 계산할때 이웃끼리 거리랑은 무관하게 그냥 집합에서 2개뽑은 조합의 수를 말한다
순서쌍중 직접적으로 연결된 이웃 순서쌍은 (2,3), (2,4), (3,5)
이웃이 존재하지 않는 경우인 특정 node의 연결성이 0인경우, 1인 경우에는 local clustering coefficient를 정의하지 않는다.
node V에서 군집이 형성될 정도를 측정한다고 보면 된다.
왜냐하면 local clustering coefficient가 클수록 node V는 연결된 이웃들이 많으면서 이웃들도 연결되는 경우가 많기 때문이다.

위 그림에서 보듯이 local clustering coefficient가 높을수록 군집에 조금 더 가깝다고 보는게 적절하다
3. global clustering coefficient
그래프의 각 node의 local clustering coefficient를 모두 더하고 그들의 평균을 구한 것이다.
local clustering coefficient가 정의되지 않는, 연결성이 0,1인 node는 제외하고 계산된다.
사실 이 때문에 연결성이 0,1인 node의 local clustering coefficient를 0으로 정의하는 경우가 있다는 것이 합리적이다.
전체 그래프에서 군집의 형성 정도를 측정한다고 보면 된다.

4. real graph의 clustering coefficient
real graph는 유난히 군집계수가 높다. 즉 군집이 유난히 많이 존재한다.
여러가지 이유로 실제 사회현상은 동질성을 반영한다.
유사한 성질을 가지는 node끼리는 link될 가능성이 높다는 것이다.

전이성을 가지는 경우도 많은데,
예를 들면 내가 2명의 서로 모르는 친구를 알고 있을 때 그 친구들끼리 소개시켜주는 경우가 사회 현상에서 흔하기 때문이다.

5. Erdős–Rényi model의 clustering coefficient
Erdős–Rényi model은 node수가 충분히 크면 clustering coefficient의 기댓값이 p에 수렴한다고 알려져있다.(증명은 상당히 어렵다..)
직관적으로 생각하면 node끼리 link가 서로 독립적으로 연결되기 때문에 하나의 군집을 만들어내기 쉽지 않다.
그럼에도 불구하고 giant connected component는 n이 충분히 크면 거의 확실하게 만들어낼 수 있다는 사실이 대단히 놀랍다...
'딥러닝 > Graph' 카테고리의 다른 글
| 그래프 전파 모형1 - 선형 임계치 모형(linear threshold model) (0) | 2024.05.10 |
|---|---|
| 그래프를 다루는 파이썬의 NetworkX 라이브러리 맛보기 (0) | 2023.08.07 |
| 그래프의 연결 요소(connected component) (0) | 2023.07.23 |
| 검색엔진의 역사를 바꾼 pagerank 알고리즘 파헤치기 (0) | 2022.10.23 |
| 그래프의 연결성(degree)에 대한 고찰 (0) | 2022.02.16 |

