1. degree
어떤 node V의 degree란 V에 연결된 link의 수
혹은 V의 neighbor의 수와 같다.
그래서 V의 degree를 $d(V)=\left | N(V) \right | $로 표기
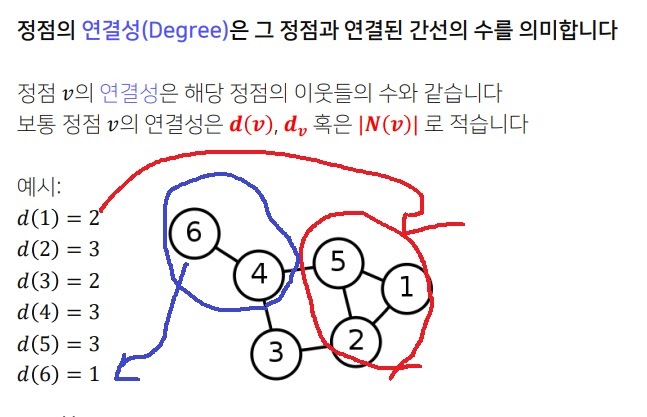
1은 2,5와 연결되어 있어서 1의 연결성은 2이다.
2. direction graph
방향성이 있는 그래프의 경우 나가는 연결성(out degree)와 들어오는 연결성(in degree)을 구분한다.
당연하겠지만 나가는 연결성(out degree)는 특정 node V에서 나가는 방향과 연결된 node의 수이고 $d_{out}(V)=\left | N_{out}(V) \right | $으로 표기
들어오는 연결성(in degree)는 특정 노드 V에 들어오는 방향으로 연결된 node의 수이고 $d_{in}(V)=\left | N_{in}(V) \right | $으로 표기

node 5에서 out neighbor는 1,2니까 $d_{out}(5)=2$
node 5에서 in neighbor는 4,2니까 $d_{in}(5)=2$
3. hub
In network science, a hub is a node with a number of links that greatly exceeds the average.
평균보다 훨씬 큰 link를 가지는 node
각 node의 link 수 평균을 구해서 그것보다 크면 hub라고 하나?? 특별한 기준이 아무리 찾아봐도 없는듯?
4. real graph의 degree distribution
두꺼운 꼬리를 가지는 분포(heavy tailed distribution)
두꺼운 꼬리를 가진다는 뜻은 link가 매우 많은 node인 hub가 거의 확실히 존재한다는 의미다.
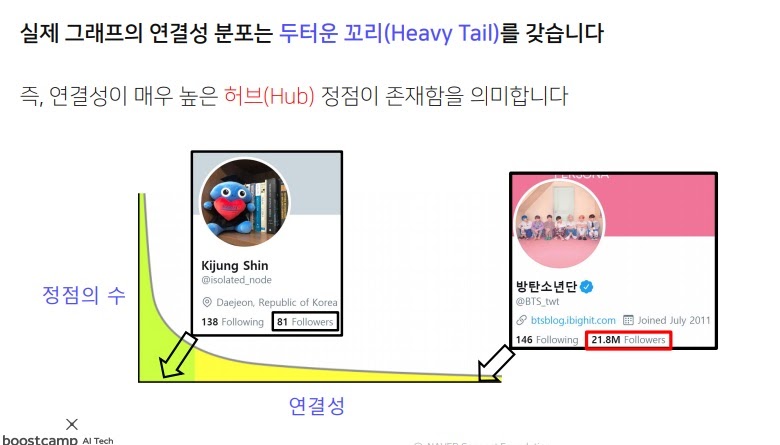
일반인(node1)의 SNS 팔로워(link) 수와 연예인(hub)의 팔로워(link) 수는 엄청난 차이가 있지
이 연예인이 바로 hub
5. Erdős–Rényi graph의 degree distribution
Erdős–Rényi graph의 degree는 이항분포를 따른다.
쉽게 생각해서 특정 node의 link가 존재할 확률이 p, 존재하지 않을 확률이 1-p이라 하자.
특정 node가 나머지 node n-1개중 어느 1개와 연결되는 사건이 성공, 그렇지 못한 사건이 실패라하면
독립적으로 일어나는 베르누이 사건으로 볼수 있어서 그렇다.

node의 수가 충분히 크면 포아송분포를 따른다고 나와있는데 그것도 결국에는 하나의 정규분포에 수렴함
node의 수가 충분히 크면 정규분포로 수렴할 것인데 그것은 link가 매우 많은 hub가 존재할 가능성이 거의 없다는 뜻이다.
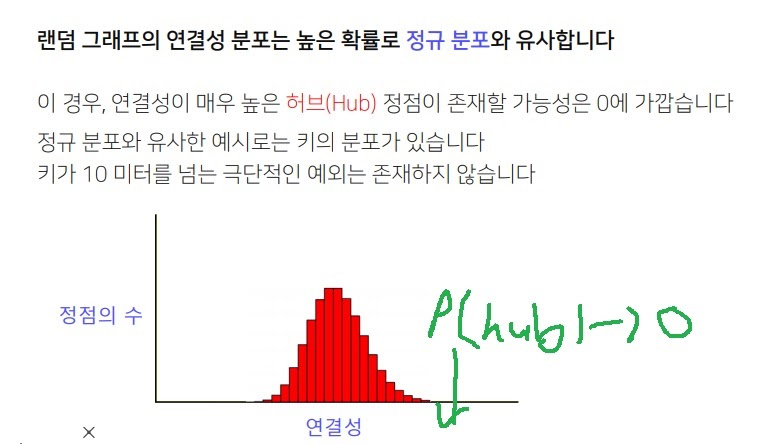
정규분포는 꼬리가 얇은 분포인데, 극단적인 점인 hub가 존재할 가능성이 낮다는 뜻이다.
참고로 random graph라고 해서 hub가 존재하지 않는 것은 아니다.
degree distribution이 두꺼운 꼬리를 가지는 scale free network라는 random graph는 hub가 존재할 가능성이 높다.
'딥러닝 > Graph' 카테고리의 다른 글
| 그래프의 연결 요소(connected component) (0) | 2023.07.23 |
|---|---|
| 검색엔진의 역사를 바꾼 pagerank 알고리즘 파헤치기 (0) | 2022.10.23 |
| 그래프에서 중심성(centrality)의 척도들 (0) | 2022.02.16 |
| 그래프의 path, distance, diameter 그리고 작은 세상 효과(small world effect) 이해하기 (0) | 2022.02.13 |
| 실제 그래프(real graph)와 랜덤 그래프(random graph) (0) | 2022.02.03 |

