1. 연결 중심성(degree centrality)
한 node에 연결된 모든 edge의 개수
weighted 그래프의 경우 모든 weight의 합
directed 그래프의 경우 incoming degree는 그 node의 인기도,
outcoming degree의 경우 그 node의 영향력 등으로 해석이 다를 수 있다.
2. eigenvector centrality(고유벡터, 위세 중심성)
연결 중심성이 오직 연결된 edge에만 의존한다는 점에서 아쉬워서 다른 node들간의 연관성도 보고 싶다는 것
그래프의 인접행렬 A와 node의 eigenvector centrality를 나타내는 벡터 $C_{e}$에 대하여 $\lambda C_{e} = AC_{e}$
를 만족시키는 $C_{e}$
$C_{e}$는 A의 eigenvector이고 $\lambda$는 A의 eigenvalue가 된다
다른 node들의 중심성까지 반영했다는 점이 특징
3. 매개 중심성(Betweenness Centrality)
중요한 node일수록 그래프의 임의의 지점에서 다른 지점으로 이동할 때 그 중요한 node를 많이 거쳐간다.
특정 node를 제외한 나머지 node들의 두 쌍 사이 모든 최단 경로중 특정 node를 포함하는 비율
link의 경우도 똑같이 계산할 수 있다. 그래프의 임의의 두 node 사이 모든 최단 경로중 해당 link를 포함하는 비율
보통 주어진 그래프에서 가장 높은 매개 중심성을 가지는 link를 반복적으로 끊어서 군집화 시키기도 한다
4. 근접 중심성(Closeness Centrality)
중요한 node일수록 다른 node까지 평균적인 거리는 짧을 것
특정 node에서 그 node를 제외한 나머지 모든 node에 대해 각각 최단 경로의 길이를 평균내고 그것의 역수를 취함
그 외에 조화 중심성, pagerank, katz 중심성 등 다양하게 있다.
5. 예시
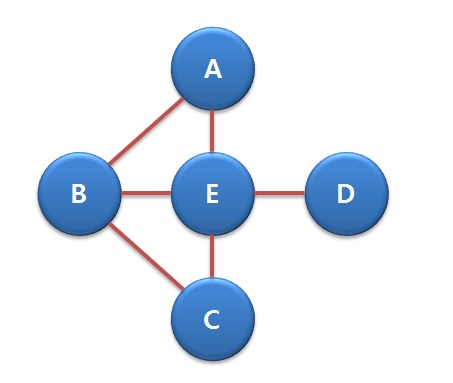
위와 같은 예시 그래프는 다음과 같은 인접행렬 A로 나타난다
\[A=\begin{pmatrix}0 & 1 & 0 & 0 & 1 \\1 & 0 & 1 & 0 & 1 \\0 & 1 & 0 & 0 & 1 \\0 & 0 & 0 & 0 & 1 \\1 & 1 & 1 & 1 & 0 \\\end{pmatrix}\]
그렇다면 각각 중심성의 정의로부터 연결중심성 $C_{d}$는
\[C_{d}=\begin{pmatrix}2 \\3 \\2 \\1 \\4 \end{pmatrix}\]
고유벡터 중심성 $C_{e}$는
\[C_{e}=\begin{pmatrix}0.882 \\1.121 \\0.882 \\0.464 \\1.247 \end{pmatrix}\]
매개 중심성 $C_{b}$
예를 들어 E를 살펴보면 E를 제외한 나머지 두 node들 사이 쌍 A-B, A-C, A-D, B-C, B-D, C-D를 먼저 고려한다
A-B의 최단 경로에는 E가 없으므로 0
A-C의 최단 경로에는 A-B-C, A-E-C로 2개가 존재하고 E를 포함하는 것은 하나이므로 비율은 0.5
A-D는 A-E-D로 오직 하나가 존재하므로 그 비율은 1
B-C는 최단 경로에 E가 없으므로 0
B-D는 B-E-D로 오직 하나가 존재하므로 그 비율은 1
C-D도 C-E-D로 오직 하나가 존재하므로 그 비율은 1
모든 총합은 3.5로 E의 매개 중심성은 3.5가 된다
이를 전부 계산하면
\[C_{b}=\begin{pmatrix}0 \\0.5 \\0 \\0 \\3.5 \end{pmatrix}\]
근접 중심성 $C_{c}$
역시 노드 E에 대해서 나머지 A,B,C,D까지 최단 거리는 전부 1이므로 평균은 1이고 이것의 역수도 1이어서
E의 근접 중심성은 1이 된다
이를 전부 계산해보면
\[C_{c}=\begin{pmatrix}0.667 \\0.800 \\0.667 \\0.571 \\1.000 \end{pmatrix}\]
노드 E가 모든 중심성 지표에서 가장 높다는 것을 확인할 수 있다
참고
https://bab2min.tistory.com/554
[네트워크 이론] 다양한 중심성(Centrality) 척도들
세상의 많은 관계들을 수학적으로 나타내는데에는 그래프만큼 강력한 도구도 없습니다. 관계의 주체가 되는 행위자들은 Node로, 관계들은 Node사이를 연결하는 Edge로 나타낼 수 있기 때문이죠. 이
bab2min.tistory.com
'딥러닝 > Graph' 카테고리의 다른 글
| 검색엔진의 역사를 바꾼 pagerank 알고리즘 파헤치기 (0) | 2022.10.23 |
|---|---|
| 그래프의 연결성(degree)에 대한 고찰 (0) | 2022.02.16 |
| 그래프의 path, distance, diameter 그리고 작은 세상 효과(small world effect) 이해하기 (0) | 2022.02.13 |
| 실제 그래프(real graph)와 랜덤 그래프(random graph) (0) | 2022.02.03 |
| 그래프를 표현하는 수학적인 방법 (0) | 2022.01.31 |

